ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.08.2024
Просмотров: 414
Скачиваний: 0
СОДЕРЖАНИЕ
Теории управления квантовыми системами.
1. Основные понятия и определения квантовой механики
1.1. Чистые и смешанные состояния
2. Элементы квантовой теории информации
2. 3. Преобразование одного кубита
2.5. Перепутывание и квантовая неразличимость
2.6. Логический элемент «управляемое не»
3. Парадокс эйнштейна – подольского – розена (эпр)
5.4 Понятие о квантовой криптографии
5.4.1. Защита посредством неортогональных состояний
5.4.2. Защита посредством перепутывания
5.4.3. Практическая реализация квантово – криптографических систем
6.2. Протокол квантовой телепортации
6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
7. Квантовые вычисления. Квантовые компьютеры.
7.4.2. Моделирование вероятности
7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
7.5. Общие требования к квантовым компьютерам Практическая реализация
Хотя
в настоящее время не опубликованы
быстрые алгоритмы решения задачи
разложения числа на простые множители,
нельзя утверждать, что они не существуют
вовсе. Кроме того, вычислительная
мощность компьютерных систем постоянно
возрастает, поэтому сложность задачи
не означает её неразрешимость. Один из
последних отчётов компании RSA посвящён
разложению 155-значного (512-битного) числа.
Вычисления велись параллельно на многих
компьютерах в течение семи месяцев в
1999 г. Если бы эта задача выполнялась на
современном персональном компьютере,
потребовалось бы 35,7 года. Оценки
показывают, что с использованием даже
тысячи современных рабочих станций и
лучшего из известных вычислительных
алгоритмов одно 250-значное число может
быть разложено на множители примерно
за 800 тысяч лет, а 1000-значное – за
![]() лет. (Для сравнения возраст Вселенной
составляет
лет. (Для сравнения возраст Вселенной
составляет![]() лет). Поэтому криптографические алгоритмы,
подобные RSA, оперирующие достаточно
длинными ключами, считались абсолютно
надёжными и использовались во многих
приложениях. Однако, если появятся
быстрые процедуры факторизации больших
целых чисел, вся секретность и надёжность
криптосистем с открытым ключом исчезнет.
лет). Поэтому криптографические алгоритмы,
подобные RSA, оперирующие достаточно
длинными ключами, считались абсолютно
надёжными и использовались во многих
приложениях. Однако, если появятся
быстрые процедуры факторизации больших
целых чисел, вся секретность и надёжность
криптосистем с открытым ключом исчезнет.
Оказывается, используя законы квантовой механики, можно построить такие компьютеры, для которых задача факторизации не составит большого труда. По оценкам квантовый компьютер с памятью объёмом всего лишь около 10 тысяч квантовых битов способен разложить 1000-значное число на простые множители в течение всего нескольких часов.
5.4 Понятие о квантовой криптографии
Технология квантовой криптографии опирается на принципиальную особенность поведения квантовой системы - невозможно одновременно измерить один параметр системы, не исказив другой. Попытка измерения взаимосвязанных параметров в квантовой системе вносит в неё нарушения, и полученная информация в результате такого измерения определяется принимаемой стороной, как дезинформация. Благодаря этому возможно построение каналов передачи данных, защищённых от подслушивания: получатель всегда сможет определить, не перехвачена ли информация, и при этом положительном ответе повторить передачу с другим ключом. Отправитель кодирует отправляемые данные, задавая определённые квантовые состояния, а получатель регистрирует эти состояния. Затем получатель и отправитель совместно обсуждают результаты наблюдений. В итоге можно быть уверенным, что переданная и принятая кодовые последовательности тождественны. Обсуждение результатов касаются ошибок, внесённых шумами или злоумышленником, и ни в малейшей степени не раскрывает содержимого сообщения.
В 1984 г. Чарльз Беннет из IBM и Жиль Брассар из Монреальского университета предположили, что фотоны могут быть использованы в криптографии для получения фундаментально защищённого канала. Для представления нулей и единиц они решили взять фотоны, поляризованные в различных направлениях, и предложили простую схему квантового распределения ключа шифрования, названную ими ВВ84. В 1991 г. идея была развита Экертом. Эта схема использует квантовый канал, по которому участники защищённого сеанса связи (Алиса и Боб) обмениваются сообщениями, передавая их в виде поляризованных фотонов.
Квантовая криптография обеспечивает абсолютно защищённое распределение ключа, поскольку, в отличие от классической криптографии, она основана на законах физики, а не на том факте, что для успешного прослушивания потребовались бы огромные вычислительные мощности.
Квантовое распределение ключа начинается с пересылки одиночного или перепутанных квантов между Алисой и Бобом. Подслушивание с физической точки зрения основано на серии экспериментов, которые подслушивающий агент Ева выполняет на носителях информации, в данном случае – на пересылаемых квантах. Согласно законам квантовой физики любое измерение, выполняемое Евой, неизбежно меняет состояние передаваемых квантов, и Алиса и Боб могут это выяснить в последующей открытой связи. Таким образом, основные составляющие квантового распределения ключа таковы: квантовый канал для обмена квантами и так называемый открытый канал, который используется, чтобы проверить, искажено ли сообщение через квантовый канал, рис. 5.2.
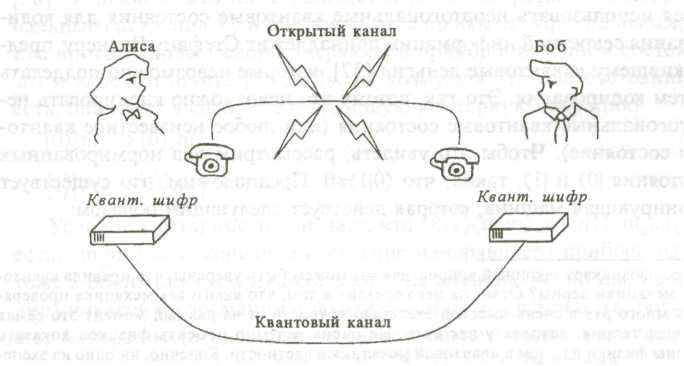
Любой открытый канал можно просматривать кому угодно, однако, при этом невозможно изменять информацию, пересылаемую через такой канал.
Во время пересылки ключ либо закодирован с использованием заданного набора неортогональных квантовых состояний одиночной частицы, либо он получается из заданного набора измерений, выполняемых на перепутанных частицах после пересылки (во время пересылки ключ ещё даже не существует).
5.4.1. Защита посредством неортогональных состояний
Идея
использовать неортогональные квантовые
состояния для кодирования секретной
информации принадлежит Стефану Визнеру
и основана на невозможности клонировать
неортогональные квантовые состояния
или любое неизвестное состояние.
Пассивный
подслушиватель не может достоверно
различить неортогональные состояния
(назовем их
![]() ),
если он не знает базиса, в котором те
были приготовлены.Рассмотрим
два нормированных состояния |0> и |1>,
таких, что <0|1>
),
если он не знает базиса, в котором те
были приготовлены.Рассмотрим
два нормированных состояния |0> и |1>,
таких, что <0|1>![]() 0.
Предположим, что существует клонирующая
машина, которая действует следующим
образом
0.
Предположим, что существует клонирующая
машина, которая действует следующим
образом
|0>|бланк>|машина>![]() |0>|0>|машина0>
|0>|0>|машина0>
|1>|бланк>|машина>![]() |1>1>|машина1>,
|1>1>|машина1>,
где «бланк» обозначает исходное состояние частицы, которое после действия машины стано-вится клоном, и где все состояния соответствующим образом нормированы. Операция клонирования должна быть унитарной и сохранять внутреннее произведение, так что
<0|1>=<0|1><0|1><машина0|машина1>,
что возможно только при <0|1>=0 (два состояния взаимно ортогональны) и <0|1>=1 (два состояния неразличимы и, следовательно, не могут быть использованы для кодирования двух различных состояний бита), что противоречит исходному предположению. Таким образом, если кто-то секретно приготавливает случайную последовательность битов |1>|0>|1>1>…., где |0> и |1> выбраны случайно, то эту последовательность невозможно достоверно воспроизвести.
Предположим,
что Ева настраивает свой измеряющий
прибор в неком исходном состоянии
![]() .
Ее цель – отличить состояния
.
Ее цель – отличить состояния![]() ,
не возмущая их. Ее действия будут
описываться следующими унитарными
преобразованиями над входными состояниями
:
,
не возмущая их. Ее действия будут
описываться следующими унитарными
преобразованиями над входными состояниями
:
![]()
![]()
Унитарность сохраняет скалярное произведение, поэтому
![]()
откуда следует, что
![]()
Это означает, что конечное состояние измерительного прибора Евы одно и то же в обоих случаях. Два состояния не возмущены, но Ева не получила никакой информации о закодированных значениях бита.
Более общее измерение, когда Ева возмущает исходные состояния, так что
![]() .
.
Тогда в результате действий подслушивателя:
![]() ,
,
![]() .
.
Условие
унитарности даёт
![]()
Наилучшая
ситуация, когда у Евы возникает самый
лучший шанс различить два состояния
своего прибора, получается, когда
скалярное произведение
![]() принимает минимальное значение. Это
происходит при <
принимает минимальное значение. Это
происходит при <![]() |
|![]() >=1,
т.е. когда два состояния |0> и |1> после
взаимодействия становятся неразличимы.
>=1,
т.е. когда два состояния |0> и |1> после
взаимодействия становятся неразличимы.
5.4.2. Защита посредством перепутывания
Концепция квантовой криптографии, основанная на перепутывании, включает в себя ЭПР - парадокс. Программа ЭПР включала в себя полноту («в полной теории должен присутствовать элемент, соответствующий каждому элементу реальности»), локальность («реальная фактическая ситуация в системе А не зависит от того, что происходит с системой В, пространственно отделённой от первой»), и определяла элемент физической реальности так: «если, никак не возмущая систему, мы можем с определённостью предсказать значение физической величины, то существует элемент физической реальности, соответствующий этой физической величине».
Программа ЭПР требовала другого описания квантовой реальности, однако до установления теоремы Белла в 1964 г. не было ясно, возможно ли такое описание, и, если да, то приведёт ли оно к другим предсказаниям результатов экспериментов. Белл показал, что предположения ЭПР о локальности, реальности и полноте несовместимы с некоторыми предсказаниями квантовой механики, касающимися перепутанных частиц.