Добавлен: 21.10.2018
Просмотров: 3253
Скачиваний: 12
28
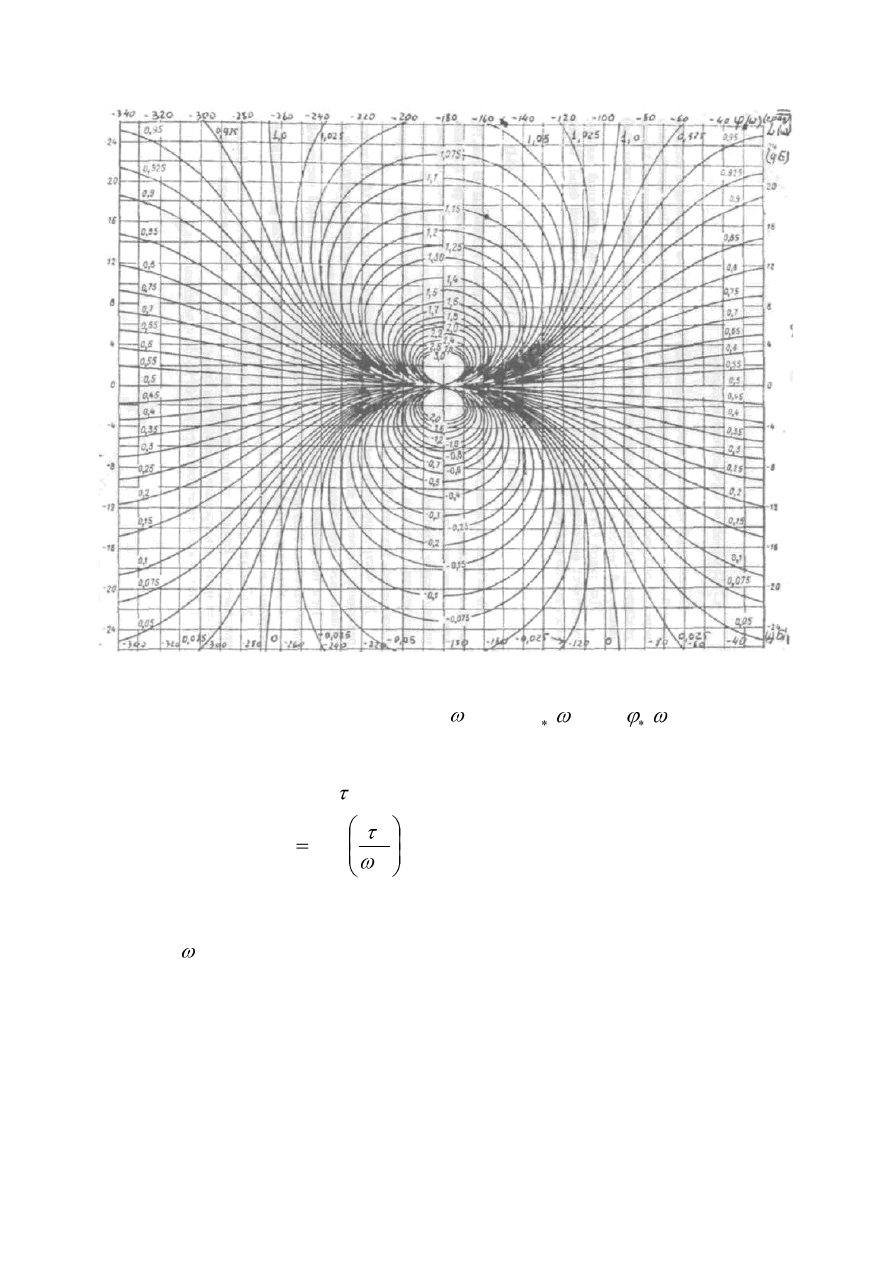
Рис. 13. Номограмма построения
)
(
P
по
)
(
L
и
)
(
разомкнутой
одноконтурной САУ с единичной обратной связью.
5. Для каждого значения
)
(
j
h
) согласно зависимости
j
i
j
j
i
j
h
P
t
y
2
)
(
(40)
определяем точки переходных характеристик для каждой трапеции и
изображаем их графики на рис. 14. В формуле (40)
j
P
- значение высоты j-ой
трапеции,
j
2
- значение частоты основания j-ой трапеции.
29
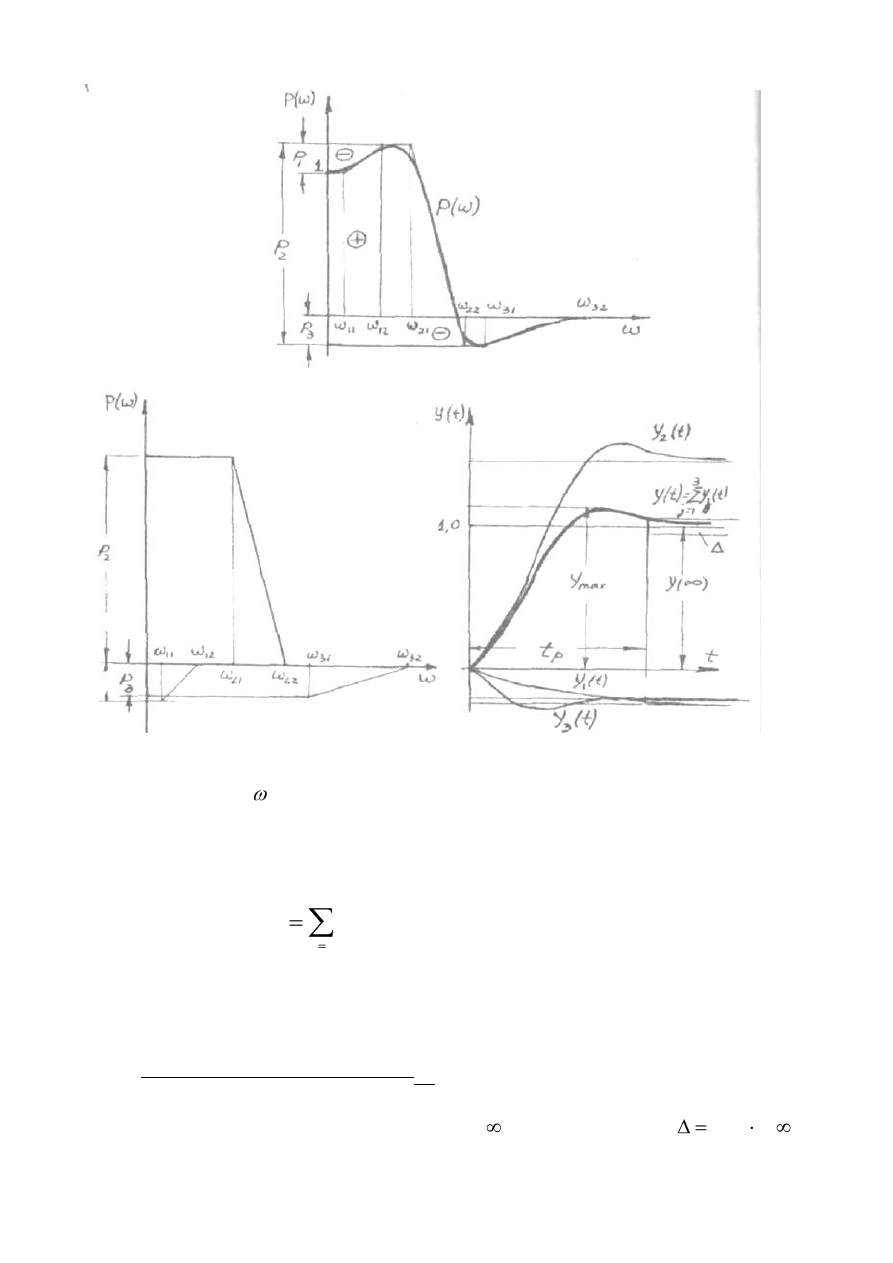
Рис 14. Этапы построения переходного процесса по вещественной частотной
характеристике
)
(
P
.
6. Переходной процесс системы получаем как сумму переходных
характеристик
)
(t
y
j
для каждой трапеции с учётом знака:
n
j
j
t
y
t
y
1
)
(
)
(
(41)
Типовой переходной процесс показан на рис. 14. По его параметрам
определяют показатели качества и сравнивают их с требуемыми по заданию.
Основные показатели качества:
- время переходного процесса
P
t - время от момента начала единичного
входного воздействия до момента, когда выходной сигнал
)
(t
y
будет
отличаться от установившегося значения
)
(
y
не более, чем на
)
(
05
,
0
y
,
т.е. когда:
30
)
(
05
,
0
)
(
)
(
)
(
y
y
y
t
y
;
- перерегулирование % :
%
100
)
(
)
(
max
y
y
y
,
где
max
y
- максимальное значение выходного сигнала САУ
)
(t
y
.
Точность построения
)
(t
y
переходного процесса зависит от точности
аппроксимации трапециями площади, ограниченной кривой
)
(
P
. Если же
основные показатели построенного переходного процесса
)
(t
y
не
соответствуют
требуемым,
то
необходимо
изменить
параметры
корректирующего звена так, чтобы устранить это несоответствие.
Например, если
P
t расчетное больше
P
t заданного, то необходимо
изменить параметры
)
(s
W
ky
с целью увеличения
С
желаемой ЛАЧХ; если %
расчетное больше требуемого, необходимо изменение
)
(s
W
высокочастотной
области ЛАЧХ и т. д.
После введенных изменений следует провести расчёт переходного
процесса
)
(t
y
с целью определений показателей качества САУ и сравнения их с
требуемыми.
б) аналитическое построение переходного процесса для САУ на основе
компьютерной системы Mathcad.
График переходного процесса строится на основе связи между
переходным процессом и вещественной частотной характеристикой замкнутой
системы. Эта связь определяется следующей зависимостью, представленной в
[2].
.
d
)
t
sin(
)
(
P
2
)
t
(
h
0
Вещественная характеристика замкнутой системы может быть найдена
следующим образом
)).
i
(
W
Re(
)
(
P
жз
Более подробно алгоритм и пример расчета переходного процесса исследуемой
САУ в системе Mathcad см. в разделе 4 .
31
3. ПРИМЕР РАСЧЕТА ЗАДАНИЯ ПО КУРСОВОЙ РАБОТЕ
ГРАФОАНАЛИТИЧЕСКИМ МЕТОДОМ
3.1. Задание на курсовую работу
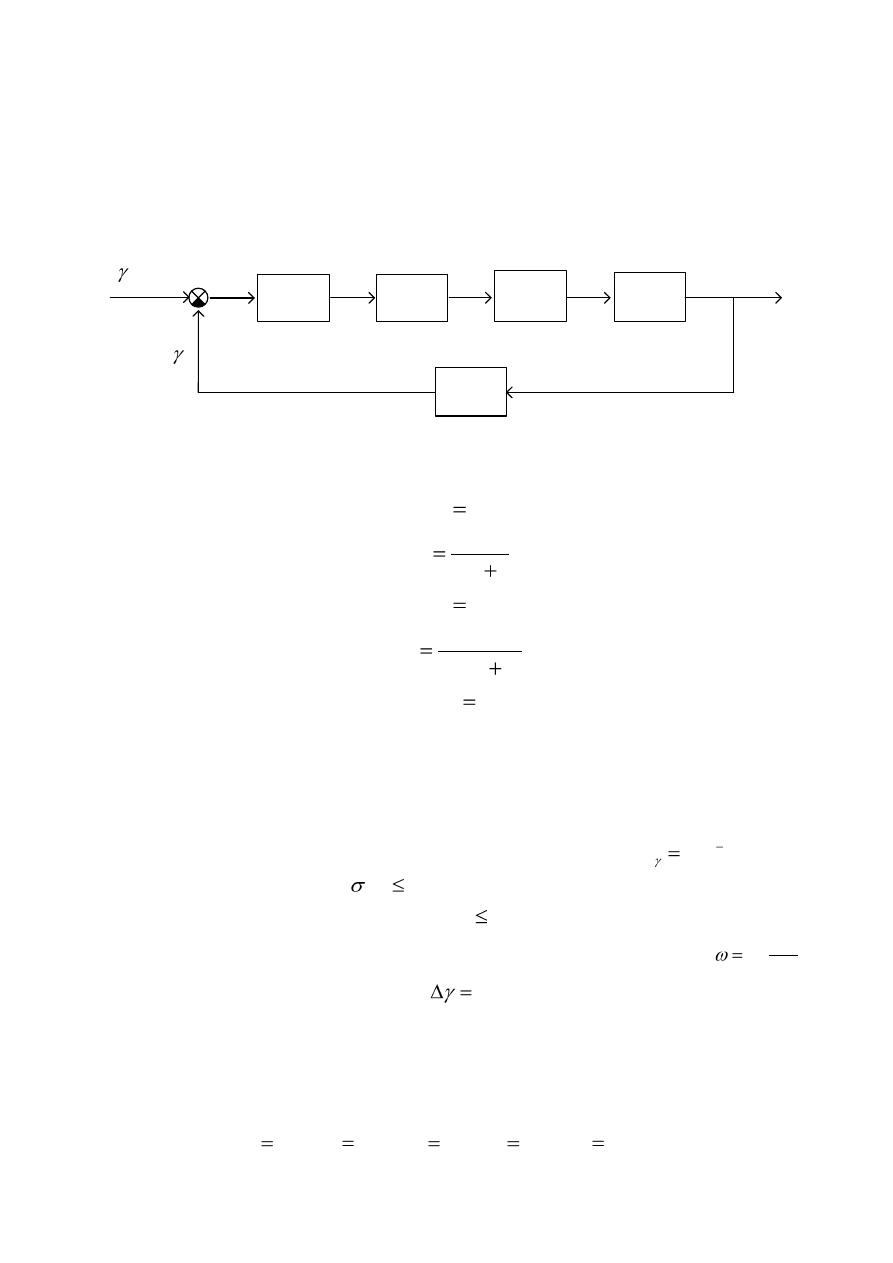
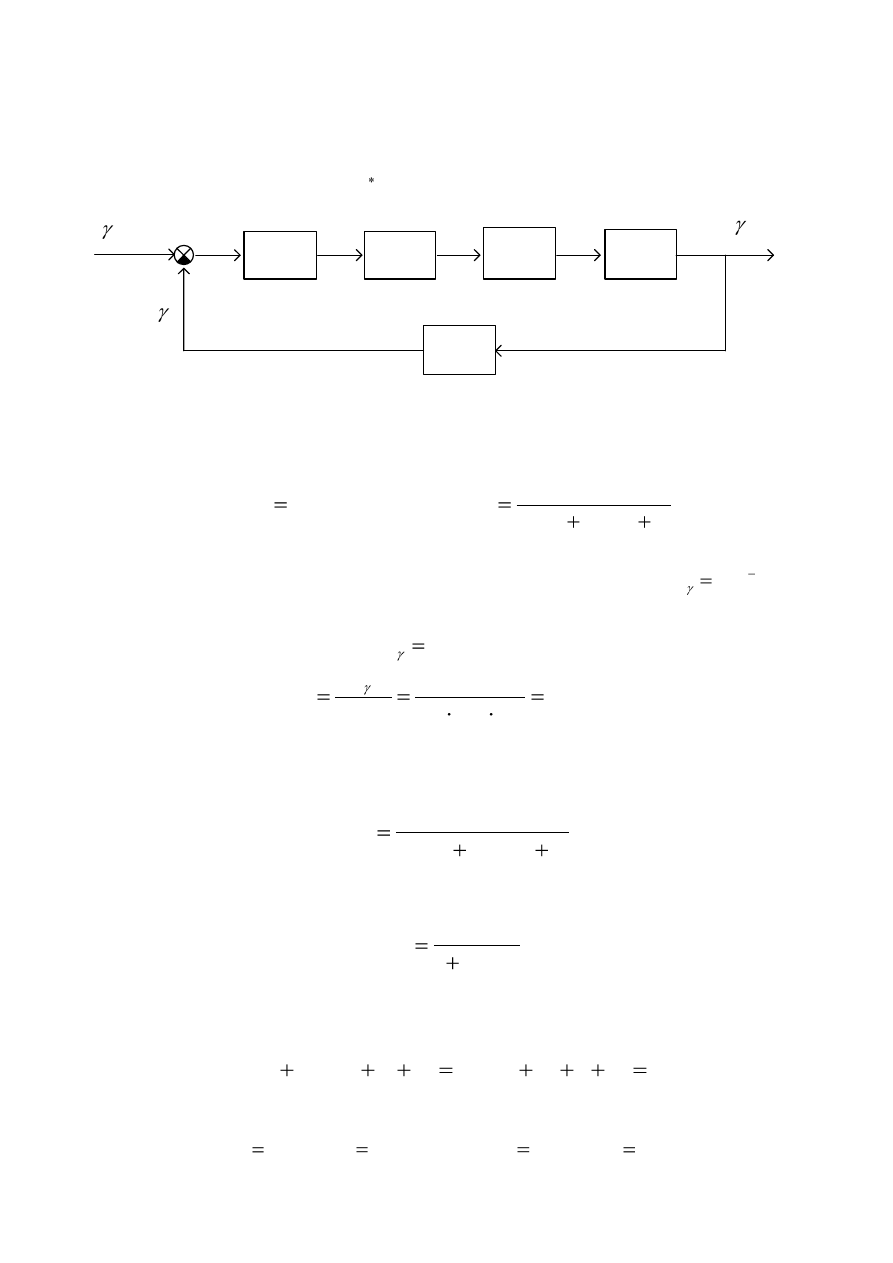
Задана структурная схема САУ ЛА по каналу крена (рис.15).
W
1
(s)
W
ky
(s)
W
2
(s)
W
3
(s)
W
4
(s)
)
(t
y
ЗАД
Рис. 15. Структурная схема САУ ЛА по каналу крена.
Передаточные функции блоков схемы:
1
1
)
(
k
s
W
;
1
)
(
2
2
2
s
T
k
s
W
;
3
3
)
(
k
s
W
;
)
1
(
)
(
4
4
4
s
T
s
k
s
W
;
?
)
(s
W
ky
Синтезировать передаточную функцию корректирующего звена
)
(s
W
ky
и
определить
3
k
в
)
(
3
s
W
так, чтобы САУ, представленная на рис. 15, обладала
следующими показателями качества:
- астатизмом первого порядка;
- передаточным коэффициентом разомкнутой системы
1
15 c
k
;
- перерегулированием
%
30
max
;
- временем переходного процесса
c
t
P
5
,
1
;
- максимальным ускорением регулируемой величины не более
2
с
рад
25
при наличии рассогласования
рад
2
,
0
.
Построить переходной процесс скорректированной системы и показать,
что система удовлетворяет заданным требованиям.
Заданные значения параметров передаточных функций:
8
,
0
1
k
;
100
2
k
;
8
,
0
4
k
;
c
T
1
,
0
2
;
c
T
9
,
0
4
.
32
3.2. Типовой графоаналитический расчет по курсовой работе
Преобразованная структурная схема с единичной обратной связью,
необходимая для построения
)
(s
W
, представлена на рис. 16.
W
1
(s)
W
ky
(s)
W
2
(s)
W
3
(s)
- 1
ЗАД
Рис. 16. Преобразованная структурная схема САУ ЛА по каналу крена.
Передаточная функция разомкнутой системы:
)
1
)(
1
(
)
(
)
(
)
(
)
(
)
(
4
2
4
3
2
1
4
3
2
1
s
T
s
T
s
k
k
k
k
s
W
s
W
s
W
s
W
s
W
Р
.
Т. к. передаточный коэффициент разомкнутой системы
1
15 c
k
, то
определяем коэффициент
3
k
из соотношения:
4
3
2
1
k
k
k
k
k
,
234
,
0
0,8
100
,8
0
15
4
2
1
3
k
k
k
k
k
Откуда передаточная функция разомкнутой нескорректированной САУ:
)
1
9
,
0
)(
1
1
,
0
(
15
)
(
s
s
s
s
W
Р
.
Тогда передаточная функция замкнутой системы
)
(
1
)
(
)
(
s
W
s
W
s
Ф
Р
Р
.
Проверяем по критерию Гурвица устойчивость заданной системы в замкнутом
состоянии. Характеристическое уравнение замкнутой системы:
0
15
09
,
0
15
)
1
9
,
0
)(
1
1
,
0
(
2
3
s
s
s
s
s
s
,
откуда коэффициенты характеристического уравнения равны:
09
,
0
0
a
;
1
1
a
;
1
2
a
;
15
3
a
.