(9.142)

(9.143)

см. рис. 9.49.

Таблица 9.24. К расчету размеров лобовых частей катушек

обмотки из прямоугольного провода

Напряжение U,B	S, 10-3, м	В, 10-3, м	Напряжение U, B	S, 10-3, м	В, 10-3, м
≤ 660	3,5	25	6000...6600	6...7	35...50
3000...3300	5...6	35...40	10000	7.. .8	60…65

Примечание. Меньшие значения для катушек с непрерывной изоляцией.

m = sin α = (b + S) / t_z; (9.144)

b — ширина меди катушки в лобовой части, м; S — допустимое рас­стояние между медью проводников соседних катушек (по табл. 9.24), м; t_z — зубцовое деление, м.

Стержневая волновая обмотка фазных роторов асинхронных дви­гателей. Длина лобовых частей стержня ротора, м,

l_л = К_л b_кт + 2В_c; (9.145)

вылет лобовой части, м,

l_выл = К_л b_кт + B_c, (9.146)

где b_кт — среднее расстояние между сторонами последовательно соединенных стержней:

b_кт = (D₂ - h_п2) / 2р; (9.147)

B_c — сумма прямолинейных участков лобовой части стержня: длины вылета из паза и длины конца стержня в месте установки хомутиков, соединяющих стержни друг с другом. Обычно принимают 0,05...0,10 м (большие значения для машин большей мощности и напряжения). Для высоковольтных двигателей мощностью 800 - 1000 кВт и более берут В_с = 0,12...0,16 м.

Коэффициенты К_л и К_выл находят соответственно по формулам (9.142) и (9.143), в которых

m = (b_cт + S_cт) / t_z2, (9.148)

где S_ст — расстояние между медью соседних стержней в лобовых час­тях, м (S_ст принимают в соответствии с табл. 9.25 в зависимости от на­пряжения на контактных кольцах ротора при неподвижной машине); b_cт — ширина меди стержня ротора, м; t'_z2 — зубцовое деление по дну пазов ротора, м:

t'_z2 = π(D₂ – 2 h_П2) / Z₂ (9.149)

Таблица 9.25. К расчету размеров лобовой части

стержней фазных роторов асинхронных двигателей

Uк.к., В	500	500...1000	1000.. .1500	1500.. .2000
Sст, 10-3 м	1,7	2	2,6	2,9

После расчета l_п определяют среднюю длину витка по (9.135) и длину всех стержней фазы обмотки по (9.134).

Активное сопротивление фазы ротора r₂ определяют по (9.132). Дня дальнейших расчетов r₂ должно быть приведено к числу витков первичной обмотки

r'₂ = v₁₂ r₂, (9.150)

где коэффициент приведения сопротивлений обмотки фазного ротора

v₁₂ = (9.151)

9.10.2. Индуктивные сопротивления обмоток двигателей

с фазными роторами

Индуктивные сопротивления обмоток статора и ротора двигате­лей с фазными роторами рассчитывают по формуле

x = 1,58 (9.152)

здесь расчетная длина l'_δ при наличии радиальных вентиляционных каналов для обмотки статора

l'_δ = l₁ - 0,5 n_k b_k (9.153)

и для обмотки ротора

l'_δ = l₂ - 0,5 n_k b_k (9.154)

при отсутствии радиальных каналов в этих формулах n_к = 0.

Входящие в (9.152) коэффициенты магнитной проводимости λ_п, λ_л и λ_д обмоток определяют следующим образом.

---

Коэффициент магнитной проводимости пазового рассеяния рас­считывают по формулам, приведенным в табл. 9.26, в зависимости от конфигурации паза и расположения в нем проводников обмотки (рис. 9.50). В этих формулах значения коэффициентов k_β и k'_β зависят от укорочения шага обмотки β, которое определяют по расчетному шагу обмотки (см. гл. 3) β = у_расч / τ.

При β = 1

k_β = k'_β = 1 (9.155)

При обмотке с укорочением 2/3 ≤ β≤ 1

k'_β = 0,25 (1 + 3β); (9.156)

при укорочении 1/3 ≤ β ≤ 2/3

k'_β = 0,25 (6β - 1). (9.157)

Коэффициент

k_β = 0,25 (1 + 3 k'_β). (9.158)

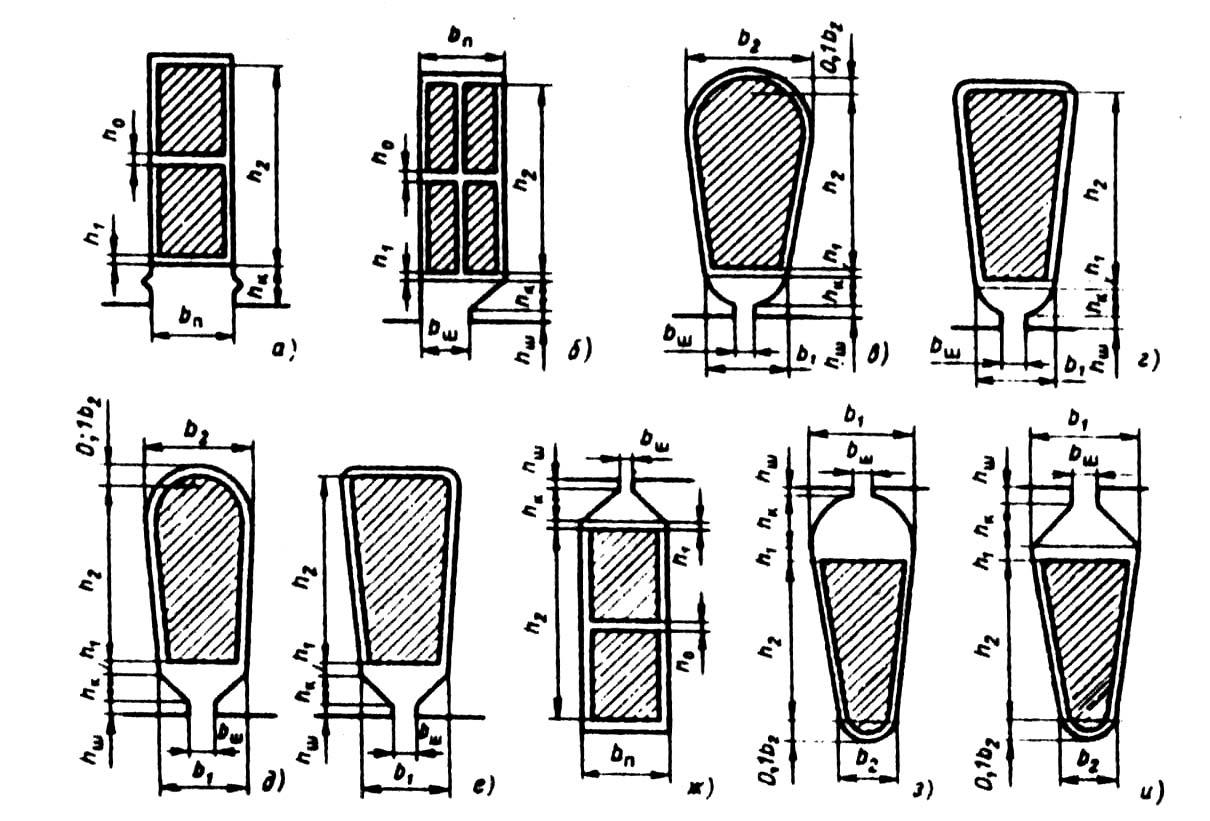
Рис. 9.50. К расчету коэффициентов магнитной проводимости пазового рассеяния

фазных обмоток:

а—е — обмотки статора; ж—и — обмотки фазного ротора

Таблица 9.26. Расчетные формулы для определения коэффициентов

магнитной проводимости пазового рассеяния обмоток статора и

фазного ротора асинхронных двигателей

Рисунок	Тип обмотки	Расчетные формулы
9.50, а	Двухслойная
	Однослойная
9.50, б	Двухслойная
9.50, в,г,з	Двухслойная и одно­слойная
9.50, д,е,и	То же
9.50, ж	Двухслойная

Коэффициент магнитной проводимости лобового рассеяния

λ_л = 0,34 (l_л – 0,64 β τ ) (9.159)

где q и l_л — число пазов на полюс и фазу и длина лобовой части витка обмотки; β = у_расч / τ — укорочение шага обмотки, для которой прово­дится расчет, т. е. обмотки статора или фазного ротора.

Коэффициент магнитной проводимости дифференциального рассеяния для обмоток статора и фазного ротора

(9.160)

Значение коэффициента ξ зависит от числа q, укорочения шага обмотки и размерных соотношений зубцовых зон и воздушного зазора.

Ниже приводятся формулы, в которые при расчете ξ, для обмо­ток статора или ротора следует подставлять данные обмоток и зубцовых зон соответственно статора или ротора.

Для обмоток статора и ротора при q, выраженном целым чис­лом (q ≥ 2), для обмотки с β = 1

ξ = 2 + 0,022 q² – k²_об(1 + Δz); (9.161)

при укороченном шаге обмотки (β < 1)

ξ = k''q² + k'_β – k²_об(1 + Δz); (9.162)

при дробном (q ≥ 2)

ξ = k''q² + 2k''_β – k²_об( + Δz); (9.163)

при дробном q, значение которого 1 < q < 2,

ξ = k''q² + 2k''_β – – k²_об(+ Δz); (9.164)

В этих формулах коэффициенты Δz, k', k" и k"_β определяют по кривым, приведенным на рис. 9.51. Для определения k"_β и k' необ­ходимо найти дробную часть числа q, равную c/d (дробное число q = b + c/d, где b — целое число, c/d < 1 — дробная часть числа q), коэффициент k'_β — по (9.156) или (9.157).

Индуктивное сопротивление обмотки фазного ротора, опреде­ленное по (9.152), должно быть приведено к числу витков обмотки статора:

х'₂ = v₁₂ x₂, (9.165)

где v₁₂ — коэффициент приведения сопротивлений по (9.151).

9.10.3. Сопротивления обмоток двигателей с короткозамкнутыми роторами

---

Активное сопротивление фазы обмотки статора двигателя с короткозамкнутым ротором рассчитывается так же, как и для двигате­ля с фазным ротором.

Активное сопротивление фазы короткозамкнутого ротора опреде­ляется следующим образом. Как говорилось выше, за фазу обмотки, выполненной в виде беличьей клетки, принимают один стержень и два участка замыкающих колец (см. рис. 9,35). Токи в стержнях и за­мыкающих кольцах различны, поэтому их сопротивления при рас­чете общего сопротивления фазы должны быть приведены к одному току. Таким образом, сопротивление фазы короткозамкнутого ро­тора r₂ является расчетным параметром, полученным из условия равенства электрических

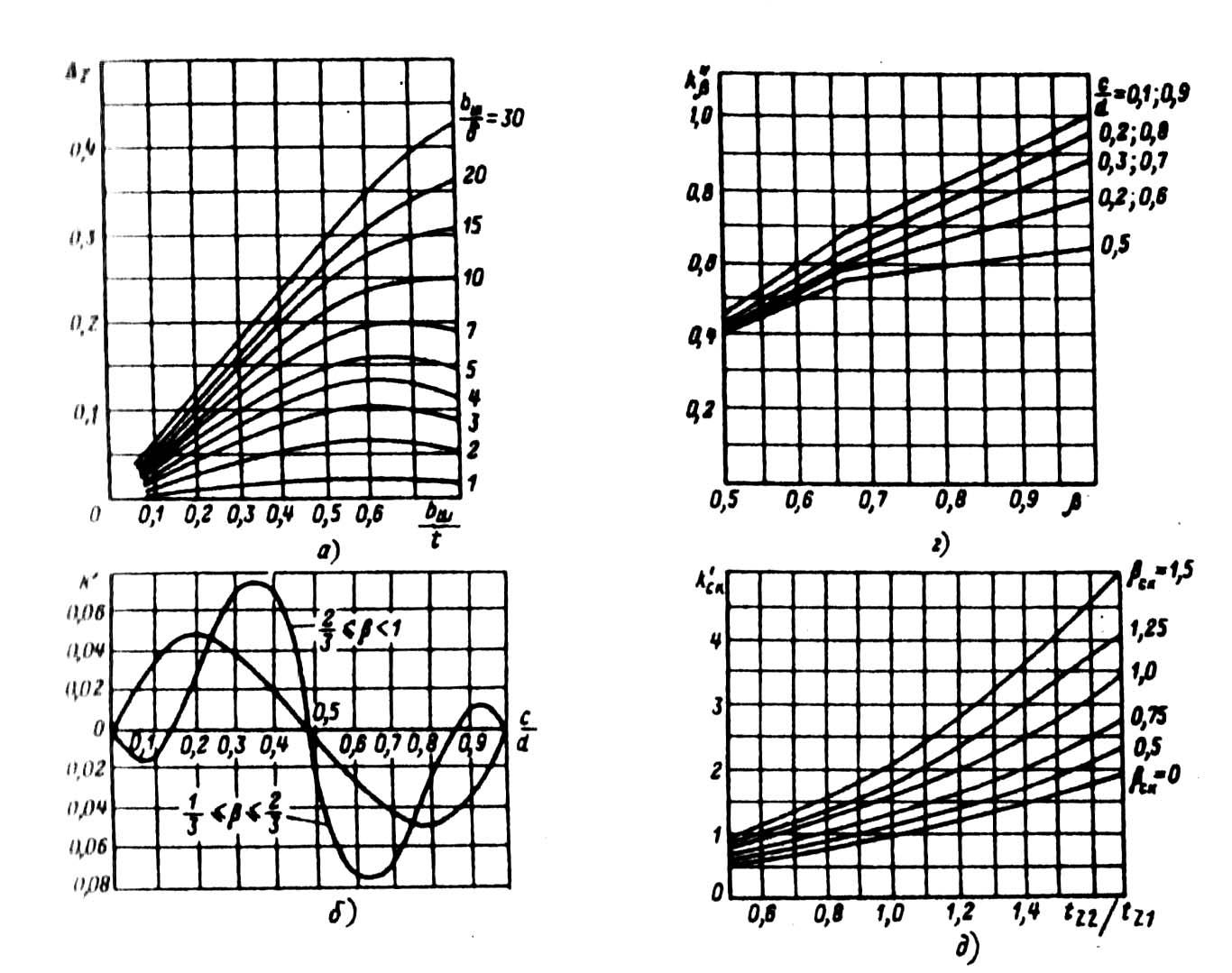
Рис. 9.51. Коэффициенты к расчету проводимости

дифференциального рассеяния:

а — коэффициент Δz в зависимости от размерных соотношений b_ш/t_z и b_ш/S;

б — коэффициент k' в зависимости от дробной части числа q;

в — коэф­фициент К' в зависимости от укорочения шага обмотки β;

г — коэффициент К''_β в зависимости от укорочения шага обмотки β и дробной части чис­ла q;

д — коэффициент k'_ск в зависимости от соот­ношения t_z2/t_z1 и относительного скоса пазов β_ck

потерь в сопротивлении r₂ от тока I₂ и сум­марных потерь в стержне и участках замыкающих колец соответственно от тока в стержне I_c и тока в замыкающем кольце I_кл реальной машины:

(9.166)

где I_с — ток в стержне ротора; I_кл — ток в замыкающих кольцах; r_C — сопротивление стержня; r_кл — сопротивление участка замыка­ющего кольца, заключенного между двумя соседними стержнями (см. рис. 9.35).

Ток I_с называют током ротора и в расчетах обозначают I₂.

Учитывая, что

I_кл = I_с /Δ = I₂ /Δ, (9.167)

где Δ = 2sin — (см. § 9.7), из (9.167), получаем

r₂ = r_с + 2 (9.168)

где

r_c = ; (9.169)

r_кл = (9.170)

В этих выражениях I_с — полная длина стержня, равная расстоя­нию между замыкающими кольцами, м; D_кл._ср — средний диаметр замыкающих колец, м (см. рис. 9.37):

D_кл._ср = D₂ - h_кл; (9.171)

q_c — сечение стержня, м²; k_r — коэффициент увеличения активного со­противления стержня от действия эффекта вытеснения тока; при рас­чете рабочих режимов в пределах изменения скольжения от холостого хода до номинального для всех роторов принимают k_r = 1; q_кл — площадь поперечного сечения замыкающего кольца, м²; р_с и р_кл — соответственно удельные сопротивления материала стержня и замыкающих колец, Ом м, при расчетной температуре (см. табл. 5.1).

Сопротивление r₂ для дальнейших расчетов должно быть приве­дено к числу витков первичной обмотки. Выражение коэффициента приведения для сопротивления фазы короткозамкнутого ротора по­лучают, подставляя в (9.151) значения m₂ = Z₂, w₂ = 1/2, k_об2 = 1 и учитывая влияние скоса пазов:

(9.172)

где коэффициент скоса пазов (по 3.17)

k_ск = 2 sin ;

Обычно значения β_ск выражают в долях зубцового деления ротора t_z2. При скосе пазов ротора на одно зубцовое деление стато­ра γ_ck = π2p / Z₁. В этом случае в двигателях с 2р = 2 из-за малости угла γ_ck принимают k_cк = 1.

---

Приведенное значение активного сопротивления фазы обмотки короткозамкнутого ротора

r'₂ = r₂ v₁₂. (9.173)

Индуктивное сопротивление рассеяния обмотки статора асинх­ронного двигателя с короткозамкнутым ротором рассчитывается по той же формуле, что и для статора с фазными роторами, т. е.

x = 1,58 (9.174)

Входящий в формулу коэффициент магнитной проводимости пазового рассеяния λ_п определяют в зависимости от конфигурации пазов по формулам табл. 9.26.

Коэффициент магнитной проводимости лобового рассеяния λ_л определяется по (9.159).

Коэффициент магнитной проводимости дифференциального рассеяния λ_д1 определяют по формуле

(9.174а)

в которой ξ, находят следующим образом.

При открытых пазах статора и отсутствии скоса статора или ротора

(9.175)

При полузакрытых или полуоткрытых пазах статора с учетом скоса пазов

(9.176)

В этих формулах t_z1 и t_z2 — зубцовые деления статора и ротора; Δ_Z определяют по кривой рис. 9.51, a, k_β определяют по (9.155) или (9.158); β_cк = β_cк/t_z2 — скос пазов, выраженный в долях зубцового деления ротора. При отсутствии скоса пазов b_ск = 0; k'_cк определяют по кривым рис. 9.51, д в зависимости от t_z2/t_z1 и β_cк (при отсутствии скоса пазов — по кривой, соответствующей β_ск = 0).

Индуктивное сопротивление обмотки короткозамкнутого ротора определяют по формуле

(9.177)

полученной после подстановки в (9.152) значений m₂ = Z₂ и q₂ = 1/(2р) обмотки короткозамкнутого ротора и введения дополнительного слагаемого λ_ск.

Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора рассчитывают по приведенным в табл. 9.27 формулам в зависимости от конфигурации паза ротора (рис. 9.52).

Таблица 9.27. Расчетные формулы для определения коэффициентов

магнитной проводимости пазового рассеяния короткозамкнутых роторов

Рисунок	Расчетные формулы
9.52, а
9.52,6
9.52, в
9.52, г
9.52, д

При расчете номинального режима двигателя во всех формулах k_д= 1.

При закрытых пазах ротора любой конфигурации (рис. 9.52, а—д) в расчетных формулах табл. 9.27 нужно при шлицах по рис. 9.52, е слагаемые h_ш /b_ш заменить на 0,3 + 1,12 • 10⁶ , по рис. 9.52, ж — на h_ш/b_ш + 1,12 • 10⁶ , где — толщина ферромагнит­ной перемычки над пазом, м; I₂ — ток ротора, А.

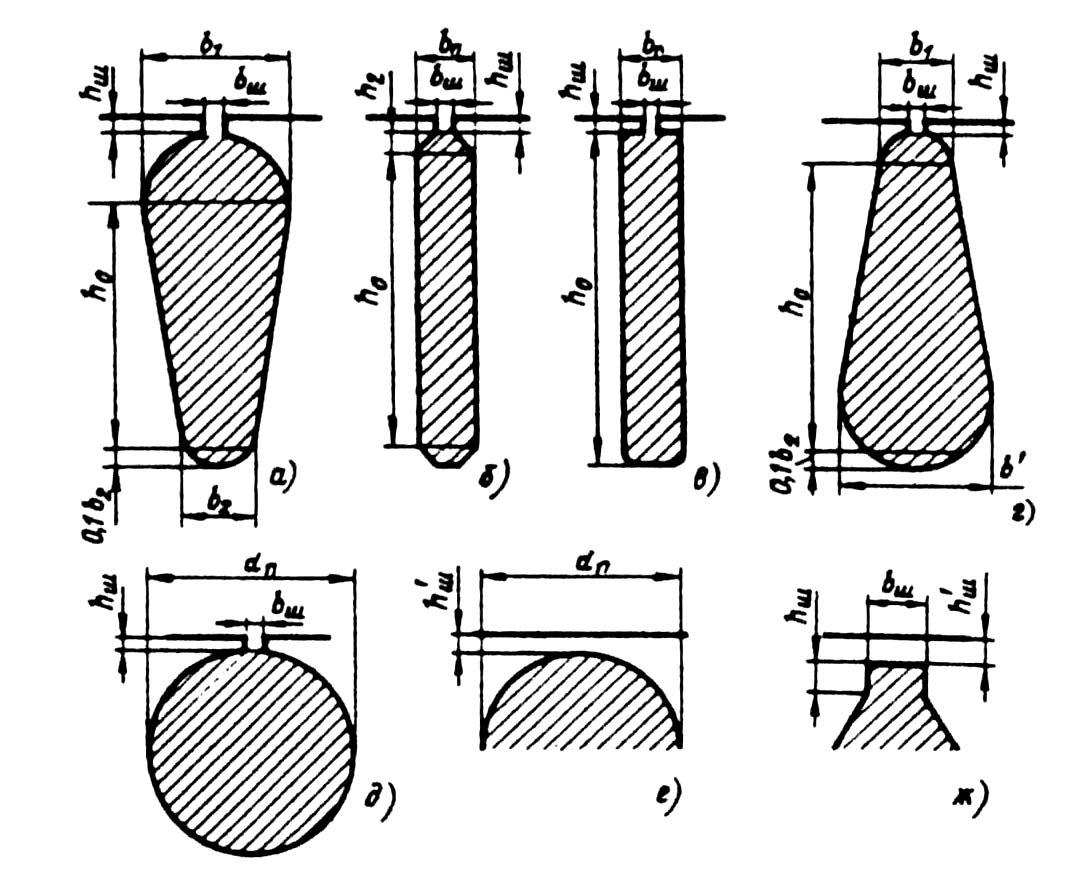
Рис. 9.52. К расчету коэффициентов магнитной проводимости

пазового рассеяния короткозамкнутых роторов:

а — д — полузакрытые пазы; е, ж — закрытые пазы

Коэффициент магнитной проводимости лобового рассеяния рассчитывают в зависимости от размеров и расположения замыкающих колец обмотки по следующим формулам.

В роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора (см. рис. 9.37, б), используют формулу

(9.178)

Если замыкающие кольца отставлены от торцов ротора (см. рис. 9.37, а), как, например, в обмотке, выполненной из медных или латунных стержней, впаянных в замыкающие кольца, расчет прово­дят по формуле

---

(9.179)

В этих формулах D_кл.ср — средний диаметр замыкающих колец по (9.171); Δ = 2 sin πρ/Z₂ — коэффициент приведения токов в кольце к току в стержне; h_кл и b_кл — средние высота и ширина колец (см. рис. 9.37); ; — по (9.154).

Коэффициент магнитной проводимости дифференциального рассеяния обмотки, короткозамкнутого ротора

(9.180)

где

(9.181)

Δ_Z находят по кривым рис. 9.51, а.

Как видно из (9.181), при большом числе пазов ротора, приходя­щихся на пару полюсов: Z₂/p ≥ 10, без заметной погрешности можно принять ξ = 1.

Коэффициент проводимости скоса, учитывающий влияние на ЭДС обмотки ротора скоса пазов,

, (9.182)

где β_ск — скос пазов, выраженный в зубцовых делениях ротора. При скосе пазов на одно зубцовое деление ротора β_ск = 1; k_μ — коэффициент насыщения магнитной цепи (по 9.129).

Приведенное к числу витков обмотки статора индуктивное со­противление обмотки короткозамкнутого ротора

х'₂ = х₂ γ₁₂ (9.183)

где v₁₂ — по (9.172).

Сопротивление схемы замещения r_μ (см. рис. 9.47, а) является расчетным. Введением его в схему замещения учитывают влияние потерь в стали статора на процессы в асинхронной машине, поэтому значение сопротивления r_μ должно быть принято таким, чтобы выделяющаяся в нем активная мощность была равна мощности, затрачиваемой на потери в стали в реальной машине и отнесенной к одной фазе. Таким образом, r_μ = Р_СТ/(m I²_0a ), так как активные потери в стали определяются активной составляющей тока холостого хода ,I_0а. Из схемы замещения r_μ = где .

Сопротивление взаимной индукции обмоток статора и ротора x_μ по схеме замещения может быть определено как x_μ = Е₁\I_μ.

В расчетной практике параллельное включение сопротивлений r_μ и х_μ оказалось удобнее заменить последовательно включенными сопротивлениями r₁₂ и х₁₂ (см. рис. 9.47, 6), значения которых опре­деляют из условия

откуда

и

Так как в асинхронных машинах r_μ ≤ x_μ, то х₁₂ ≈ х_μ, а r₁₂ << х₁₂. В связи с этим значение r₁ не играет заметной роли при анализе процессов в машине, и в расчетах им часто пренебрегают.

Сопротивления r₁ и х₁₂ с достаточной для обычных расчетов точностью определяют по следующим формулам:

r₁₂ = P_cт.осн / (m I²_μ) ; (9.184)

(9.185)

9.10.4. Относительные значения параметров

Для удобства сопоставления параметров отдельных машин и упрощения расчета характеристик параметры асинхронных машин выражают в относительных единицах, принимая за базисные значе­ния номинальное фазное напряжение и номинальный фазный ток статора.

Значения параметров, выраженные в относительных единицах, отмечают звездочкой:

(9.186)

Относительные значения одних и тех же параметров схемы замещения различных асинхронных двигателей нормального исполне­нии незначительно отличаются друг от друга.

Так, относительные значения индуктивных сопротивлений рассеяния обмотки статора и приведенного сопротивления обмотки ротора большей частью находятся в пределах х₁ = 0,08...0,14 и х'₂ = 0,1...0,16.

---

Смотрите также файлы

• Глава 11 Проектирование машин постоянного тока.doc

• Глава 12 Системы автоматизированного проектирования электрических машин.doc

• Обложка.doc

• Огавление.doc

• Предисловие.doc