ВУЗ: Алтайский Государственный Университет
Категория: Учебное пособие
Дисциплина: Управление проектами
Добавлен: 23.10.2018
Просмотров: 15196
Скачиваний: 56
Модуль «Управление программами и проектами» 10З
трех работ 1—2, 1—3, 1—4, соединим результаты этих стрелок через зависи
мость и сведем их к событию 4, откуда берут начало все работы по оценке
обстановки.
Наносим на матрицу работу 8, технология работ которой (см. перечень
работ) зависит от всех работ, оценивающих обстановку. В связи с этим объе
диняем результаты всех работ в одно событие при помощи зависимости. За
канчиваем построение фрагмента сетевой матрицы путем нанесения остав
шихся в перечне работ (9—12).
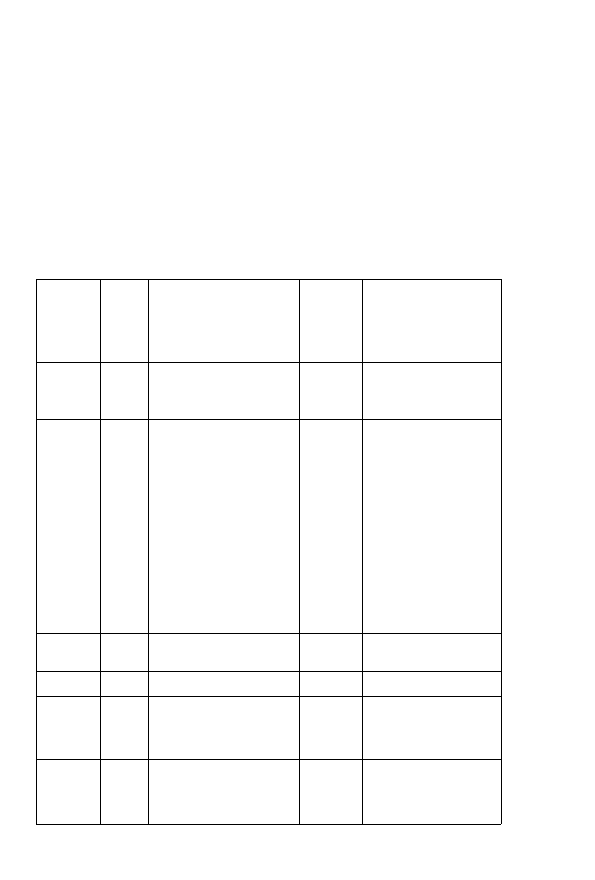
Таблица 3.1
Перечень работ
Номер
предшест
вующей
работы
-
2 - 7
8
9
10
Номер
данной
работы
1
2
3
4
5
6
7
8
9
10
11
Содержание
данной
работы
Определение замысла
и цели действий
Оценка обстановки:
по кадрам
по финансово-экономическим
ресурсам
по технике
по мощности оборудования
и энергоресурсам
по производительности труда
и заработной плате
по социальным вопросам
Прогнозирование результата
Информационный цикл
Анализ фактического
распределения прав и
обязанностей в аппарате
управления треста
Рассмотрение результатов
анализа
Ориенти
ровочная
продолжи
тельность,
дн.
2
2
3
3
2
1
2
1
1
4
3
2
Исполнитель
Управляющий трестом,
главный инженер,
общественные
организации
Начальник отдела кадров
Начальник финансового
и планово-экономического
отделов
Главный инженер
Начальник технического
отдела
Начальник технического
отдела, главный механик,
главный энергетик
Начальник отдела труда
и заработной платы
Управляющий трестом,
общественные
организации
Управляющий трестом,
главный инженер
Все исполнители
Управляющий трестом,
главный инженер
Управляющий трестом,
главный инженер,
общественные
организации
104 Управление развитием организации: модульная программа для менеджеров
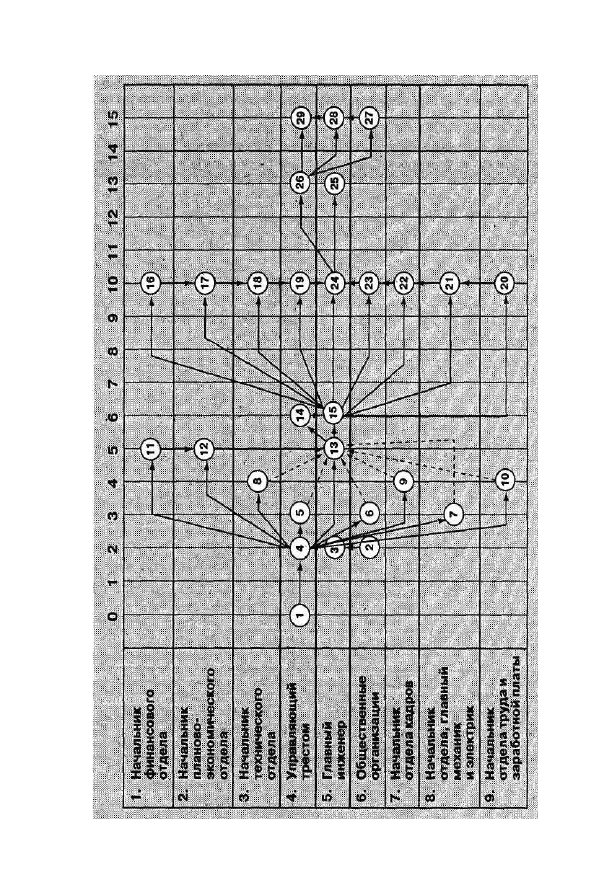
Рис
. 3.4
. Сетева
я
матриц
а
Модуль «Управление программами и проектами» 105
работы
плюс ее продолжительность (t
j - i
).
равняется минимальному (min) позднему на-
Важнейшее преимущество сетевой матрицы состоит в том, что
отпадает необходимость производить расчеты параметров матриц,
так как они наглядно показаны на рис. 3.4. Но знать, как рассчиты
ваются эти параметры, необходимо, поскольку это позволяет осу
ществлять в проектах маневрирование ресурсами, повышает уро
вень эффективности управления.
Остановимся кратко на расчете важнейших параметров сетевых
графиков.
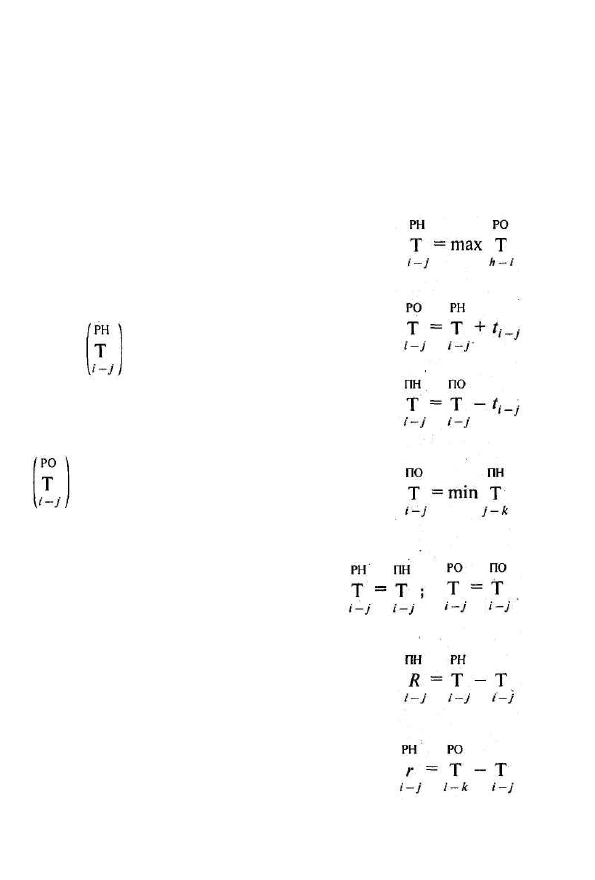
Время раннего начала (РН) данной работы
(i=j) равняется максимальному (max) времени ран
него окончания (РО) непосредственно предшеству
ющих ей работ (j - i).
Время раннего окончания (РО) данной работы
(j - i) равняется времени раннего начала данной
Время позднего начала (ПН) данной работы
(i - j) равняется времени ее позднего окончания
(ПО) минус ее продолжительность (t
i - j
).
Время позднего окончания данной работы
чалу (ПН) непосредственно следующих за ней ра
бот (j - k).
Эти равенства характерны для критиче
ских, т.е. самых напряженных, работ, выпол
нение которых обязательно в строго установ
ленные сроки, так как критические работы
не имеют резервов времени.
Этот алгоритм определяет полный резерв вре
мени данной работы (R
i -j
); он показывает, на ка
кое время можно отодвинуть начало данной работы
либо увеличить ее продолжительность, не изменяя
общего срока выполнения проекта.
Этот алгоритм определяет частный резерв вре
мени данной работы (r
i -j
); он показывает, на какое
время можно отодвинуть начало данной работы
либо увеличить ее продолжительность, не изменяя
раннего начала непосредственно следующих за ней

10б Управление развитием организации: модульная программа для менеджеров
работ. На сетевой матрице этот резерв изображен волнистой линией
(точками и др.).
Этот алгоритм определяет коэффици
ент напряженности работы (К
н
), где R
i - j
—
полный резерв времени; t
кр
— общая про
должительность критического пути; t
кр
(с) —
продолжительность критических работ,
совпадающих с максимальным путем, в состав которого входит ра
бота, для которой определяется К
н
.
Знание коэффициента напряженности позволяет математичес
ки определять ответственность каждого менеджера проекта за вы
полнение той или иной работы проекта по всем иерархическим
уровням управления. '
Поскольку для построения сетевой матрицы нужно определить
время выполнения каждой операции, то возникает необходимость
научно обоснованного формирования оценок времени в условиях за
данных ограничений по ресурсам. Рекомендуется определять продол
жительность выполнения работ на основе вероятностного метода. Для
этого необходимо правильно выбрать соответствующий закон рас
пределения вероятностей, которому подчинена продолжительность
выполнения операций.
Установлено, что наилучшее распределение продолжительнос
ти работ согласуется с законом нормального распределения случай
ных величин. Но поскольку определение кривой распределения и
других параметров — процесс довольно трудоемкий, то в практике
моделирования используются следующие упрощенные формулы:
где t
HB
— наиболее вероятная продолжительность выполнения дан
ной операции; t
оп
— «оптимистическая» продолжительность выпол
нения данной операции; t
nc
— «пессимистическое время» выполне
ния данной операции; t
р
— реальная продолжительность данной
операции.
Определение продолжительности выполнения работ осуществ
ляется, как правило, методом экспертных оценок.

Модуль «Управление программами и проектами» 107
Таким образом, у обеих работ в сетевой матрице будет одна и та же
продолжительность, но будут ли они выполнены в определенное расчетное
время? Такая уверенность, безусловно, выше по работе «б». Следовательно,
за ходом выполнения работы «а» необходимо установить четкий контроль.
Чтобы контролировать весь процесс с помощью сетевой матрицы, необхо
димо определить еще один параметр, а именно математическое ожидание
квадрата отклонения случайной величины от математического ожидания
случайной величины, т.е. дисперсию случайной величины о. Эта величина
и будет характеристикой степени неопределенности выполнения действий
в ожидаемое время.