Файл: Контрольные работы. Теория автоматического управления.docx
ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Методичка
Дисциплина: Теория автоматического управления
Добавлен: 19.10.2018
Просмотров: 5339
Скачиваний: 88
шестого варианта – в табл. 6.
5. Реализация цифровых регуляторов методом последовательного
программирования по варианту 29 таблицы 3.
Вариант №30
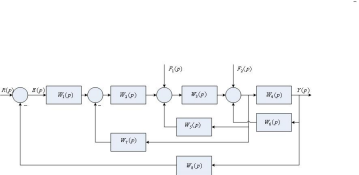
1. Определите передаточную функцию по каналу возмущения
 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:
2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
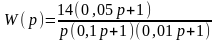 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры регулятора системы с апериодической реакцией,
состоящей из функционально необходимых элементов. Структурная схема
системы приведена на рис. 5, исходные данные для шестого варианта –
в табл. 7.
5. Реализация цифровых регуляторов методом параллельного
программирования по варианту 30 таблицы 3.
Вариант №31
1. Определите передаточную функцию по каналу возмущения
 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:

2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
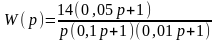 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры ПИД – регулятора по временному
модифицированному методу Зиглера – Никольса системы, состоящей
из функционально необходимых элементов. Структурная схема
системы приведена на рис. 2, исходные данные для седьмого варианта –
в табл. 2.
5. Реализация цифровых регуляторов методом прямого программирования
по варианту 31 таблицы 3.
Вариант №32
1. Определите передаточную функцию по каналу управления
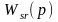 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:

2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
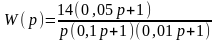 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры ПИД – регулятора по частотному методу Зиглера –
Никольса системы, состоящей из функционально необходимых элементов.
Структурная схема системы приведена на рис. 2, исходные данные для
седьмого варианта – в табл. 4.
5. Реализация цифровых регуляторов методом последовательного
программирования по варианту 32 таблицы 3.
Вариант №33
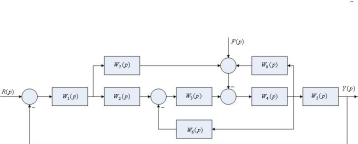
1. Определите передаточную функцию по каналу возмущения
 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:
2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
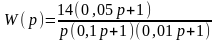 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры ПИД – регулятора по методу CHR системы,
состоящей из функционально необходимых элементов. Структурная схема
системы приведена на рис. 3, исходные данные для седьмого варианта –
в табл. 5.
5. Реализация цифровых регуляторов методом параллельного
программирования по варианту 33 таблицы 3.
Вариант №34
1. Определите передаточную функцию по каналу управления
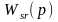 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:

2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры регулятора по критерию модульного
(технического) оптимума системы, состоящей из функционально
необходимых элементов. Структурная схема системы приведена на рис. 4,
исходные данные для седьмого варианта – в табл. 6.
5. Реализация цифровых регуляторов методом прямого программирования
по варианту 34 таблицы 3.
Вариант №35
1. Определите передаточную функцию по каналу возмущения
 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:

2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры регулятора системы с апериодической реакцией,
состоящей из функционально необходимых элементов. Структурная схема
системы приведена на рис. 5, исходные данные для седьмого варианта –
в табл. 7.
5. Реализация цифровых регуляторов методом последовательного
программирования по варианту 35 таблицы 3.
Вариант №36
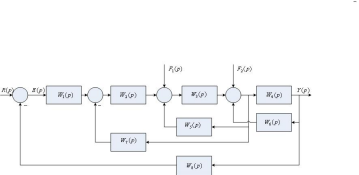
1. Определите передаточную функцию по каналу возмущения
 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:
2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры ПИД – регулятора по временному
модифицированному методу Зиглера – Никольса системы, состоящей
из функционально необходимых элементов. Структурная схема
системы приведена на рис. 2, исходные данные для восьмого варианта –
в табл. 2.
5. Реализация цифровых регуляторов методом параллельного
программирования по варианту 36 таблицы 3.
Вариант №37
1. Определите передаточную функцию по каналу управления
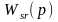 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:
2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры ПИД – регулятора по частотному методу Зиглера –
Никольса системы, состоящей из функционально необходимых элементов.
Структурная схема системы приведена на рис. 2, исходные данные для
восьмого варианта – в табл. 4.
5. Реализация цифровых регуляторов методом прямого программирования
по варианту 37 таблицы 3.
Вариант №38
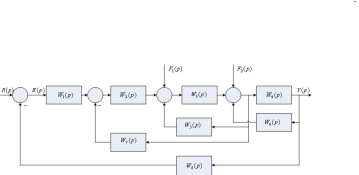
1. Определите передаточную функцию по каналу возмущения
 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:
2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
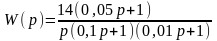 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры ПИД – регулятора по методу CHR системы,
состоящей из функционально необходимых элементов. Структурная схема
системы приведена на рис. 3, исходные данные для восьмого варианта –
в табл. 5.
5. Реализация цифровых регуляторов методом последовательного
программирования по варианту 38 таблицы 3.
Вариант №39
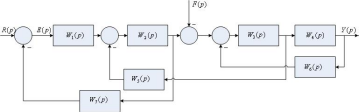
1. Определите передаточную функцию по рассогласованию
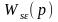 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:
2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
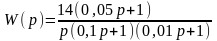 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры регулятора по критерию модульного
(технического) оптимума системы, состоящей из функционально
необходимых элементов. Структурная схема системы приведена на рис. 4,
исходные данные для восьмого варианта – в табл. 6.
5. Реализация цифровых регуляторов методом параллельного
программирования по варианту 39 таблицы 3.
Вариант №40
1. Определите передаточную функцию по каналу управления
 следующей
алгоритмической структуры САУ:
следующей
алгоритмической структуры САУ:
2. Постройте ЛЧХ звена, передаточная функция которого имеет вид
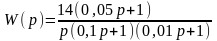 .
.
3. Проведите анализ устойчивости по критерию Гурвица системы,
состоящей из функционально необходимых элементов, структурная
схема которой приведена на рис. 1, а исходные данные для 5-го варианта
– в табл. 1.
4. Настройте параметры регулятора системы с апериодической реакцией,
состоящей из функционально необходимых элементов. Структурная
схема системы приведена на рис. 5, исходные данные для восьмого
варианта – в табл. 7.
5. Реализация цифровых регуляторов методом прямого программирования
по варианту 40 таблицы 3.
Приложение 1
Способы определения передаточных функций замкнутых САУ
-
Преобразование сложной структурной схемы в эквивалентную простую одноконтурную на основании правил преобразования и определение передаточной функции по известным формулам.
-
Аналитический вывод передаточных функций замкнутых САУ.
Составлять уравнение, связывающее изображение регулируемой функции с изображениями внешних воздействий, следует последовательно путём последовательного анализа схемы, начиная с регулируемой функции и двигаясь против направления передачи сигналов. От каждого сумматора схему необходимо осматривать в нескольких направлениях : до какого-либо из внешних воздействий или до регулируемой функции. При этом изображение выходной функции каждого звена выражается через его передаточную функцию и изображение входного воздействия, а изображение суммы нескольких слагаемых выражается через сумму их изображений. Постепенно исключаются изображения промежуточных переменных и получается искомое уравнение.
-
Применение теории графов.
Передаточные функции сложной многоконтурной САУ можно определить по структурной схеме без приведения её к одноконтурной, если использовать метод теории графов. Структурную схему САУ можно рассматривать как один из видов графа, и для определения передаточных функций пользоваться формулой Мейсона, предложенной в 1953 году:

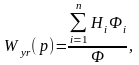 (1)
(1)
где
 отношение
изображений Y(p)
переменной y
к изображению R(p)
переменной
r
;
отношение
изображений Y(p)
переменной y
к изображению R(p)
переменной
r
;
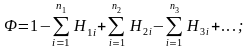
 передаточная
функция разомкнутой цепи i
-го
замкнутого контура структурной схемы;
передаточная
функция разомкнутой цепи i
-го
замкнутого контура структурной схемы;
 -
число замкнутых контуров в схеме;
-
число замкнутых контуров в схеме;
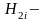 произведение
передаточных функций разомкнутых цепей
i
–й
пары несоприкасающихся замкнутых
контуров;
произведение
передаточных функций разомкнутых цепей
i
–й
пары несоприкасающихся замкнутых
контуров;
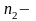 число
пар несоприкасающихся контуров;
число
пар несоприкасающихся контуров;
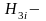 произведение
передаточных функций разомкнутых цепей
произведение
передаточных функций разомкнутых цепей
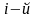 тройки
несоприкасающихся контуров;
тройки
несоприкасающихся контуров;
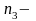 число
троек несоприкасающихся контуров;
число
троек несоприкасающихся контуров;
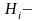 передаточная
функция
передаточная
функция
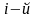 прямой
цепи от переменной
прямой
цепи от переменной
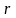 к
переменной
к
переменной
 ;
;
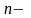 число
прямых цепей от
число
прямых цепей от
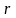 к
к

 -
функция
-
функция
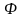 для той части структурной схемы, которая
не соприкасается с
для той части структурной схемы, которая
не соприкасается с
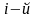 прямой цепью от
прямой цепью от
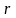 к
к
 .
.
Формула (1) позволяет без преобразования структурной схемы САУ определить любую её передаточную функцию, т.е. отношение изображения одной из переменных (обобщённых координат) к изображению внешнего воздействия или другой переменной.
Используя формулу Мейсона, нужно иметь в виду следующее:
-
Прямые цепи от
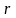 к
к
 могут частично совпадать одна с другой;
могут частично совпадать одна с другой; -
При определении передаточной функции разомкнутой цепи каждого из контуров нужно учитывать знак обратной связи, образующей этот контур;
-
Контуры не соприкасаются один с другим, когда у них нет ни общей координаты (стрелки на структурной схеме), ни общего звена (прямоугольника на структурной схеме);
-
Если в структурной схеме есть более трёх несоприкасающихся контуров, то при вычислении функции
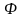 нужно добавить соответствующие суммы;
нужно добавить соответствующие суммы; -
Каждая из функций
 вычисляется так же, как и функция
вычисляется так же, как и функция
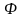 ,
но рассматривается лишь та часть
структурной схемы, которая не соприкасается
с
,
но рассматривается лишь та часть
структурной схемы, которая не соприкасается
с
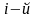 прямой
цепью от
прямой
цепью от
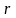 к
к
 ;
; -
Если с
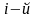 прямой
цепью соприкасаются все замкнутые
контуры, то
прямой
цепью соприкасаются все замкнутые
контуры, то
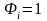 .
.
Пример
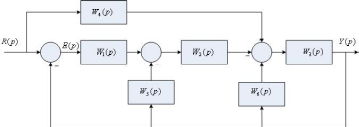
По структурной схеме САУ (рис.1) нужно определить её передаточную функцию относительно задающего воздействия r.

Рис. 1. Структурная схема многоконтурной САУ с дополнительной
связью по задающему воздействию
Воспользуемся
формулой (1) и начнём с вычисления функции
Ф.
В рассматриваемой схеме пять замкнутых
контуров; передаточные функции их
разомкнутых цепей
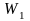 ,
,
 ,
,
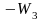 ,
,
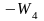 ,
,
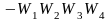 .
.
Следовательно:
 .
.
Очевидно, что схема содержат пары из 1-го и 2-го, 1-го и 3-го, 1-го и 4-го, 2-го и 4-го несоприкасающихся контуров, поэтому
 .
.
Имеется только одна тройка из несоприкасающихся контуров, и она состоит из 1-го,2-го и 4-го контуров:
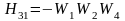 .
.
Четырёх несоприкасающихся контуров в схеме нет, следовательно, теперь можно определить функцию
 .
.
От задающего воздействия r к регулируемой координате y идут две прямые цепи передачи сигнала. Их передаточные функции
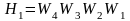 и
и
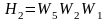 .
.
С первой прямой цепью соприкасаются все замкнутые контуры, со второй прямой цепью не соприкасается только 4-й контур, следовательно,
 и
и
 ;
;
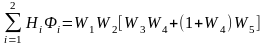 .
.
Теперь можно определить искомую передаточную функцию
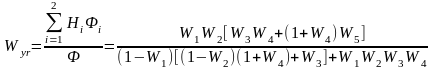 .
.
Легко убедиться, что преобразование рассмотренной структурной схемы в эквивалентную одноконтурную имеет более сложный расчёт. Использование формулы (1) обычно уменьшает трудоёмкость определения передаточных функций САУ, структурная схема которой имеет несколько взаимосвязанных контуров.
4. Применение таблиц эквивалентного преобразования структурных схем, приводимых в учебных пособиях.
Приложение 2
Методика построения логарифмических частотных характеристик САУ
Пусть
передаточная функция разомкнутой
статической САУ, состоящей из
минимально-фазовых звеньев 1-го порядка,
имеет вид
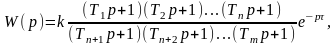 в реальных системах n(m-n).
в реальных системах n(m-n).
Отобразим
W(р) в область преобразований Фурье
преобразуем математическое описание
каждого элементарного звена к форме
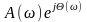 и расположим в порядке убывания величины
Тi:
и расположим в порядке убывания величины
Тi:

Тогда
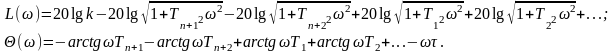

Алгоритм построения ЛАЧХ
-
На оси нанесите точки i=1/Ti. Проведите через эти точки вертикальные штриховые линии.
-
Проведите контурную линию с ординатой 20lgk слева до первой вертикальной линии при отсутствии нулевых полюсов и нулей в передаточной функции или линию с наклоном -20дБ/дек через точку
 при одном нулевом полюсе, или линию с
наклоном -40 дБ/дек через точку
при одном нулевом полюсе, или линию с
наклоном -40 дБ/дек через точку
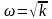 при двух нулевых полюсах, или линию с
наклоном +20 дБ/дек через точку
при двух нулевых полюсах, или линию с
наклоном +20 дБ/дек через точку
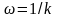 при одном корне числителя, равном нулю,
или линию с наклоном +40 дБ/дек через
точку
при одном корне числителя, равном нулю,
или линию с наклоном +40 дБ/дек через
точку
 при двух нулях, равных нулю, и т.д.
при двух нулях, равных нулю, и т.д. -
До следующей вертикальной линии проведите контурную линию с наклоном -20* дБ/дек ( – количество элементарных звеньев с одинаковыми Ti), если звенья апериодические, или +20* дБ/дек для дифференцирующих звеньев первого порядка.
-
Уменьшите (увеличьте) наклон на -20* дБ/дек (+20* дБ/дек) на следующей вертикальной линии до полного построения L().