Файл: Математические модели принятия решений - УЧЕБНЫЕ МАТ-2018.docx
Добавлен: 29.10.2018
Просмотров: 3000
Скачиваний: 29
СОДЕРЖАНИЕ
Тема 1.1. Классификация и принципы. Моделирование процессов и решений.
1.1.1. Основные понятия теории принятия решений. Историческая справка.
1.1.2. Технология решения прикладных задач поддержки принятия решений.
1.1.3. Место исследования операций в математическом моделировании.
1.1.5. Понятие математической модели принятия решений
1.1.6. Моделирование процессов
1.2.1. Производственные функции
1.2.2. Задача оптимального среднесрочного плана развития производства
Тема 1.3. Математические модели поддержки принятия решений в условиях риска и неопределенности.
1.3.1. Принципы обоснования решений в условиях риска и неопределенности.
1.3.2. Портфельный анализ: модель Марковица.
1.3.3. Инструментальные средства портфельного анализа
2.1.1. Модель контроля с одним ЛПР
2.1.2. Модель выборочного контроля с одним ЛПР
2.1.3. Модель контроля с двумя ЛПР
2.1.4. Игра «Государство-Предприниматели»
2.2.1. Минимаксные стратегии: игра двух лиц
2.2.2. Ситуации равновесия по Нэшу и Штакельбергу: игра двух лиц
2.3.1. Поле игры. Гипотезы поведения игроков
Раздел 3. Прикладные модели принятия решений: примеры
Тема 3.1. Оптимизация бонуса менеджеров производственной и финансовой компаний.
3.1.1. Модель поведения работника на рабочем месте
3.1.2. Модель оптимизации бонуса менеджеров производственных и финансовых компаний
3.2.1. Математическая модель планирования объединения предприятий.
3.2.2. Имитационная модель планирования объединения промышленных предприятий
3.4. Децентрализованная модель управления в корпорациях использует рыночный механизм, центр устанавливает внутрифирменные цены, лимиты. Каждое предприятие «покупает» часть ресурса, который необходим для достижения собственных целей. Решения о количестве приобретаемого ресурса предприятия принимают самостоятельно.
3.5. Координация решений в иерархических системах – согласование решений участников совместной деятельности, включает согласование целей, зон ответственности, распределения общих ресурсов, совместного дохода и др.
3.6. Корпорация – объединение n юридических лиц плюс (как правило) одна управляющая компания.
3.7. Математическая модель активности работника – формула зависимости фактической трудовой активности работника (ФТА, т.е. объема работы, который работник выполнит в среднем за рабочий день при сдельной системе оплаты его труда) от уровня расценки, заданной работодателем.
3.8. Математическая модель планирования объединения промышленных предприятий записывается как задача блочного линейного программирования. Она включает систему локальных ограничений (равенств и неравенств) для каждого предприятия корпорации и систему глобальных ограничений по ресурсам управляющей компании. Модель планирования объединения имеет блочно-диагональную структуру системы ограничений.
3.9. Метод Данцига-Вульфа – один из методов решения задач блочного линейного программирования.
3.10. Нормативная величина фактической трудовой активности (ФТАН) – количественное выражение объема работы, который работник (среднерыночного и индивидуального) по расчету выполнит в среднем за рабочий день при среднерыночных условиях сдельной системы оплаты его труда. Этот показатель используется при идентификации математической модели поведения работника и определяется по формуле: ФТАН = Т*ккв*кин, где Т – продолжительность рабочего дня данного работника, в рабочих часах ; ккв, кин – индексы квалификации и интенсивности труда.
3.11. Потенциал трудовой активности работника – ПТА–количественное выражение предельной трудовой активности работника (среднерыночного и индивидуального) как объема работы, который работник способен выполнить в среднем за рабочий день. Этот показатель используется при идентификации математической модели поведения работника и определяется по формуле: ПТА = ФТАН /α, где ФТАН – нормативная величина фактической трудовой активности данного работника, час.; α – среднерыночный коэффициент интенсивности труда рассматриваемого локального рынка, который может дифференцироваться по группам работников. Оценка для рынка труда г. Барнаула: α = 0.7. Для среднерыночного работника г. Барнаула при 8 часовом рабочем дне этот показатель имеет значение: ПТА = 8/0.7=11.4.
3.12. Формула трудовой активности – количественное выражение ФТА – фактической трудовой активности работника – как объема работы, который работник выполнит в среднем за рабочий день при сдельной системе оплаты его труда в зависимости от уровня расценки (руб./ЧНТ), заданной работодателем.
3.13. Часовая норма труда (ЧНТ) – количественный показатель объемов работы работников на локальном рынке труда, определяется как объем работы, который среднерыночный работника выполняет в течение одного рабочего часа. Показатель используется в математической модели активности работников в трудовых процессах как измеритель объема работ. Количественно его значение равно норме выработки. Для работников ряда профессиональных групп показатель ЧНТ выражается в натуральных единицах (для токаря, в числе изготовленных деталей в среднем за рабочий час; для землекопа – в кубических метрах котлована; для маляра – в квадратных метрах обработанной поверхности при требуемом качестве). Однако для многих профессий указать натуральный состав и количество выполненных работ не представляется возможным. В ряде таких случаев работодатель оценивает нормативный объем работы в конечных результатах (для наемного попрошайки – величина собранной милостыни; для рыбака – пойманной рыбы; для менеджера – ?). Наблюдение за трудовыми процессами показывают, что грамотные и эффективные работодатели всегда имеют инструменты оценки объемов работ и трудовых затрат своих работников. В математических моделях результативность (объемы работ) оценивается числом часовых норм труда. Различаем объем работы как задание работника до начала трудового процесса и как фактическая его активность после его завершения.
1 Оскорбин Н.М. Математическое моделирование социальных и экономических систем по произведениям А.С. Пушкина // Ломоносовские чтения на Алтае – 2012: сборник научных статей международной молодежной школы-семинара, Барнаул, 20-23 ноября. – Барнаул : АлтГПА, 2012. – Ч. II. – С. 280–286.
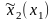
2 Наглядным примером «знака» является слово «вулкан», который вызывает соответствующие реальности ассоциации различных образов.
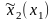
4 Экономический человек – условное общее понятие, представление о человеке как о рационально мыслящем субъекте, строящем свои планы и действия, исходя из принципа получения максимальной выгоды (Современный экономический словарь, 1997, с. 397).
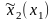
5 В литературе задача (1.1) носит название задачи математического программирования.
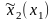
6 Основными участниками корпоративного управления выступают Собственники и Исполнительная дирекция. Собственники для защиты своих интересов на собраниях акционеров создают Совет внешних директоров, который при эффективном механизме корпоративного управления самостоятельным ЛПР не является. При этом всеми ресурсами корпорации (за исключением бюджета Совета внешних директоров и установленных границ компетенции) распоряжается Исполнительная дирекция.
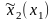
7 Дж. фон Нейман, О. Моргенштерн. Теория игр и экономическое поведение. – М.: Наука, 1970. – 708 с.
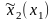
8 В теории игр ЛПР называют игроками, целевые функции – функции выигрышей, варианты решений – стратегиями, полный набор решений – ситуацией игры. Выигрыш каждого игрока зависит от сложившейся ситуации.
9 Минимизируемые показатели следует рассматривать с отрицательным знаком.
10 В рассматриваемом случае термин «неопределенность используется в двух смыслах. В названии подраздела «Модели решений с 1 ЛПР в условиях природной неопределенности», этот термин обозначает отсутствие информации у ЛПР при обосновании решений относительно параметров модели (1.1). Во втором случае этот термин используется тогда, когда неконтролируемые параметры случайными не считаются и предполагается, что они принадлежат заданному множеству.
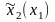
11 В теории принимается, что ЛПР частично информировано только о значениях функции полезности решений.
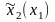
13 В рамках 5 факторной модели фирмы ресурсами являются труд, капитал, земля, информация, предпринимательский потенциал.
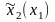
15 Рекомендуется выполнить Упражнение на стр. 10 для исследования способа решения двухкритериальной задачи принятия решений, к которой относится модель Марковица.
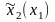
16 Здесь и далее полагаем, что в математических задачах экстремумы существуют.
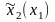
17
Предполагается, что
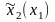– функция, определенная на множестве
стратегий игрока 1.
18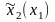
Подробнее ознакомиться с моделью
поведения работника на рабочем месте
можно по учебному пособию: Булатова,
Г.А. Методы и математические модели
управления персоналом [Текст] : учебное
пособие / Г.А. Булатова, А.С. Маничева,
Н.М. Оскорбин. – Барнаул : Изд-во Алт.
ун-та, 2015. – 108 с. (файл прилагается в
МОДУЛ).
19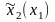
Смотрите подробнее: Оскорбин Н.М.,
Хвалынский Д.С. Декомпозиция экстремальных
задач на основе метода Данцига-Вульфа
// Ломоносовские чтения на Алтае : сборник
научных трудов Международной молодежной
школы-семинара, 5-8 ноября 2013. – Барнаул:
Из-во Алт. ун-та, 2013. – С. 199-203. Оскорбин
Н.М. и др. (файл «Оскорбин ИТ-НГУ-2010.pdf»
прилагается).