Модель Марковица предписывает выбор оптимального вектора 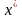долей, при котором средняя доходность портфеля должна быть не меньше заданной инвестором величины 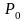(ограничение на критерий 1), а уровень риска отклонения доходности от средней величины был бы минимальным (минимизация критерия 2)¹⁵. Математически модель записывается с использованием выражений (1.19), (1.21), (1.22) в следующем виде. Найти 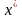из условий:

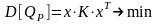; (1.23)

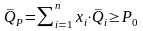; (1.24)

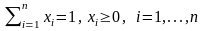. (1.25)

Упражнение. Доказать, что средний уровень доходности портфеля 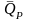изменяется в пределах: 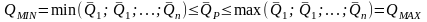, т.е. от минимальной средней 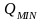до максимальной средней 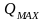доходностей выбранных активов:

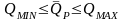. (1.26)

Рассмотрим уровни риска для оценок реальной доходности портфеля. Обозначим границы доходности портфеля: %Низ и %Верх. Математическая статистика дает следующие доверительные интервалы для реальной доходности портфеля (см. формулу (3.2)):

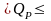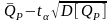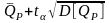%Низ %Верх, где %Низ = ; %Верх = . (1.27)

Здесь 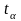– квантиль распределения доходности, определяемый заданным уровнем доверительной вероятности (для нормального распределения 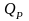и уровня значимости 5% ).

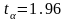Задание к вопросу экзамена 1.3.2. Портфельный анализ. Задание в МОДУЛ.

Справочно: Смотри глоссарий (Приложение 2) пп. 2.2 – 2.7.

1.3.3. Инструментальные средства портфельного анализа

Поиск оптимального портфеля с использованием математической модели Марковица (1.23) – (1.25) требует найти оценки ее параметров и обосновать нижнее значение неравенства (1.24). Эти задачи решаются с использованием компьютерной модели в среде Excel путем формирования таблицы вариантов инвестиционных портфелей при разных значениях 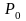в границах, задаваемых неравенством (1.26).

Методические основы портфельного анализа в среде Excel с использованием инструмента «Поиск решения» в условиях стабильной и нестабильной экономик представлены в описании соответствующих индивидуальных расчетных работ, которые приведены в электронном курсе ММПР-РН в разделе Задание к вопросу экзамена 1.3.2.

При подготовке ответа на вопрос об инструментальных средствах портфельного анализа необходимо пояснить расчетные формулы, особенности программирования инструмента «Поиск решения» и описать порядок расчетов в случае стабильной и нестабильной экономик.

Раздел 2. Теоретико-игровые математические модели принятия решений в условиях
риска и неопределенности

Примеры математических моделей. Модель контроля с одним ЛПР. Модель выборочного контроля с одним ЛПР. Модель контроля с двумя ЛПР. Игра «Государство-Предприниматели». Принципы выбора оптимальных стратегий в бескоалиционных играх (минимаксные стратегии, ситуации равновесия, устойчивые парето-оптимальные стратегии). Поле игры. Построение поля игры на примерах игры «Государство-Предприниматели» и на примере игры системы контроля.

Тема 2.1. Примеры математических моделей. Модель контроля с двумя ЛПР. Игра «Государство-Предприниматели».

2.1.1. Модель контроля с одним ЛПР

Рассмотрим поведение исполнителей в системах контроля. Пусть исполнителю поручено подготовить сообщение о параметрах реального процесса 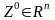, а исполнитель оценивает состояние объекта контроля как 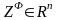, т.е. допускает ошибку:

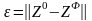, (2.1)

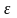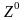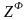где – некоторое «расстояние» между точками и в -мерном пространстве.

Идеальная работа исполнителя реально требует определенных затрат, поэтому для поддержания исполнительности в механизмах контроля предусматривается штраф, который считается пропорциональным величине ошибки. Тогда поведение исполнителя, т.е. выбор им величины 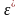, минимизирует его общие издержки. Простейшей является следующая модель исполнителя:

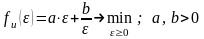. (2.2)

Здесь первое слагаемое – штраф за не исполнительность, второе – трудозатраты на подготовку сообщения. Оптимальное решение исполнителя находим решением задачи (2.2):

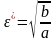. (2.3)

2.1.2. Модель выборочного контроля с одним ЛПР

В модели поведения исполнителя (2.2) предполагалось, что каждое задание исполнителя контролируется по факту его исполнения. На практике используется механизм выборочного контроля, при котором исполнитель оценивает вероятность контроля p, но не знает, что его ожидает контроль очередного исполнения. Возникает проблема принятия решения в условиях риска, которую формализуем следующей математической моделью:

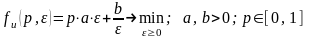. (2.2)

Используя принцип осреднения при обосновании стратегии исполнителя, получим следующее решение:

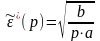. (2.4)

2.1.3. Модель контроля с двумя ЛПР

Предполагаем, что частоту контроля выбирает контрольный орган (Центр) из условия минимизации затрат на контроль и потерь в системе из-за погрешности исполнения задания. Получаем модель выбора решений с 2 ЛПР в следующем виде:

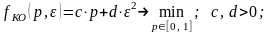. (2.5)

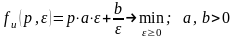. (2.6)

В выражении (2.5) первое слагаемое отражает затраты на контроль, а второе – системные потери от неидеального исполнения порученного задания.

2.1.4. Игра «Государство-Предприниматели»

Рассматриваем идеальное (модельное) общество, в котором предприниматели способны в год получать валовую прибыль 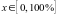. Налоговый механизм обеспечивает отчисление государству доли 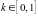прибыли. Найти оптимальное значение параметра 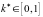, при котором государство имеет максимальные налоговые поступления.

В данном примере:

● Объект управления: механизм сбора налогов на доходы предпринимателей.

● Цель управления: максимум налоговых поступлений.

● Управляемый параметр: доля прибыли, отчисляемая предпринимателями государству.

В рассматриваемой проблемной ситуации взаимодействуют 2 игрока: государство и предприниматель, а сама игра известна в литературе как игра «Государство-Предприниматели». Игра задается следующими выражениями:

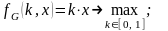. (2.7)

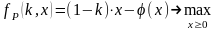. (2.8)

Функция 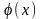в выражении (2.8) носит название предпринимательских рисков и издержек по защите бизнеса, по компенсации социальных потерь предпринимателями и др. Из содержательной интерпретации эта функция неотрицательна, прогрессивно возрастает с ростом аргумента и асимптотически приближается к потенциалу предпринимательской активности. Уровень предпринимательского потенциала для нашей модельной страны можно принять за 100%. Одной из простых функций, удовлетворяющей этим свойствам, является логарифмическая функция :

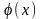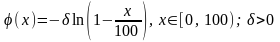. (2.9)

Упражнение. Покажите, что функция (2.9) удовлетворяет перечисленным выше свойствам и имеет нулевое значение при 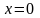. Привести содержательную характеристику функции .

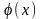Рассмотрим один из очевидных способов решения игры (2.7), (2.8), который (будут показано ниже) соответствует ситуациям равновесия по Штакельбергу.

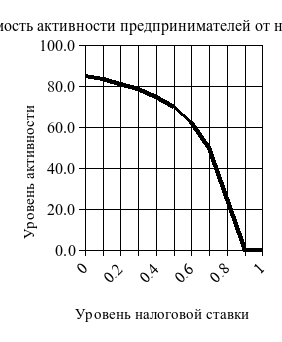
Рассчитываем валовую прибыль предпринимателей для различных 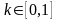(рис. 2.1).

.

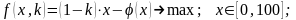
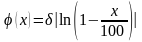Находим 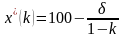, если .

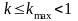В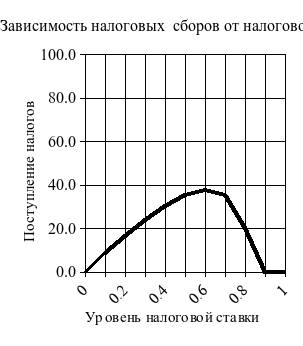 ыделяем в доходе предпринимателей налоговую долю 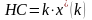(рис. 2.2).

Как видим, математическая модель налоговых сборов определяется параметром 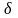– это уровень нереализованной активности предпринимательства при нулевой налоговой ставке. Полагаем 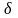=15%. Получим следующие показатели системы, характеризующие механизм налоговых сборов.