Файл: Математические модели принятия решений - УЧЕБНЫЕ МАТ-2018.docx
Добавлен: 29.10.2018
Просмотров: 3004
Скачиваний: 29
СОДЕРЖАНИЕ
Тема 1.1. Классификация и принципы. Моделирование процессов и решений.
1.1.1. Основные понятия теории принятия решений. Историческая справка.
1.1.2. Технология решения прикладных задач поддержки принятия решений.
1.1.3. Место исследования операций в математическом моделировании.
1.1.5. Понятие математической модели принятия решений
1.1.6. Моделирование процессов
1.2.1. Производственные функции
1.2.2. Задача оптимального среднесрочного плана развития производства
Тема 1.3. Математические модели поддержки принятия решений в условиях риска и неопределенности.
1.3.1. Принципы обоснования решений в условиях риска и неопределенности.
1.3.2. Портфельный анализ: модель Марковица.
1.3.3. Инструментальные средства портфельного анализа
2.1.1. Модель контроля с одним ЛПР
2.1.2. Модель выборочного контроля с одним ЛПР
2.1.3. Модель контроля с двумя ЛПР
2.1.4. Игра «Государство-Предприниматели»
2.2.1. Минимаксные стратегии: игра двух лиц
2.2.2. Ситуации равновесия по Нэшу и Штакельбергу: игра двух лиц
2.3.1. Поле игры. Гипотезы поведения игроков
Раздел 3. Прикладные модели принятия решений: примеры
Тема 3.1. Оптимизация бонуса менеджеров производственной и финансовой компаний.
3.1.1. Модель поведения работника на рабочем месте
3.1.2. Модель оптимизации бонуса менеджеров производственных и финансовых компаний
3.2.1. Математическая модель планирования объединения предприятий.
3.2.2. Имитационная модель планирования объединения промышленных предприятий
Тема 2.2. Принципы выбора оптимальных стратегий в бескоалиционных играх (минимаксные стратегии, ситуации равновесия, устойчивые парето-оптимальные стратегии).
2.2.1. Минимаксные стратегии: игра двух лиц
Пусть
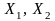 – множества стратегий игроков, а
– множества стратегий игроков, а
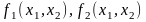 – их функции выигрышей соответственно.
Математическая модель выбора оптимальных
стратегий запишется так:
– их функции выигрышей соответственно.
Математическая модель выбора оптимальных
стратегий запишется так:
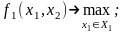 .
(2.10)
.
(2.10)
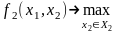 .
(2.11)
.
(2.11)
Минимаксную стратегию
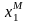 игрока 1 находим из следующей математической
задачи16:
игрока 1 находим из следующей математической
задачи16:
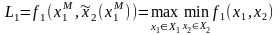 (2.12)
(2.12)
Здесь
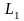 – гарантированный выигрыш первого
игрока;
– гарантированный выигрыш первого
игрока;
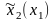 – оценка стратегии (реакции) партнера
в зависимости от выбора стратегии
– оценка стратегии (реакции) партнера
в зависимости от выбора стратегии
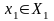 .
Эта функция в теории игр имеет смысл
функции наказания (наступления).
Минимаксную стратегию называют защитной
стратегией.
.
Эта функция в теории игр имеет смысл
функции наказания (наступления).
Минимаксную стратегию называют защитной
стратегией.
Минимаксную стратегию
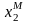 игрока 2 находим аналогично:
игрока 2 находим аналогично:
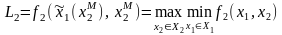 (2.13)
(2.13)
Описание переменных выражения (2.13) аналогично описанию (2.12).
Если каждый из игроков выбирает
минимаксную стратегию, то действительная
ситуация в игре
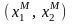 и оценки выигрышей игроков
и оценки выигрышей игроков
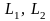 отличаются от ожидаемых (расчетных)
значений.
отличаются от ожидаемых (расчетных)
значений.
Упражнение. Покажите
справедливость неравенств:
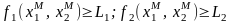 .
.
2.2.2. Ситуации равновесия по Нэшу и Штакельбергу: игра двух лиц
Минимаксные стратегии игроков в современной теории игр рекомендуются игрокам в качестве защитного поведения и в качестве оценок гарантированных результатов. Ситуации равновесия (если они существуют) предпочтительнее для игроков. Они могут реализоваться в игре при следующих условиях: игроки согласны на обмен информацией по их поиску (согласны на переговоры); игроки согласны их реализовать (выполняют условие обязующего соглашения).
Ситуация
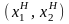 в игре (2.10), (2.11) называется ситуацией
равновесия по Нэшу, если:
в игре (2.10), (2.11) называется ситуацией
равновесия по Нэшу, если:
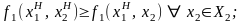 .
(2.14)
.
(2.14)
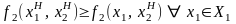 . (2.15)
. (2.15)
Упражнение. Докажите
неравенства:
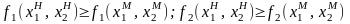 .
.
Для игр (2.10), (2.11) находят ситуации равновесия по Штакельбергу в предположении, что один из игроков наделен правом первого хода. Это право может быть институциональным (как в игре «Государство-Предприниматели») или по условиям рыночной ситуации, например, в отношениях работника и работодателя.
Предположим, что ведущим
является игрок 1 и что он знает реакцию
второго игрока
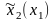 на свои решения17.
Ситуация
на свои решения17.
Ситуация
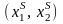 в игре (2.10), (2.11) называется ситуацией
равновесия по Штакельбергу, если она
найдена решением следующих задач:
в игре (2.10), (2.11) называется ситуацией
равновесия по Штакельбергу, если она
найдена решением следующих задач:
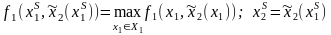 . (2.16)
. (2.16)
Упражнение. Поясните
схему поиска ситуации
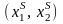 на примере игры «Государство-Предприниматели»
(рис. 2.1 и 2.2).
на примере игры «Государство-Предприниматели»
(рис. 2.1 и 2.2).
Тема 2.3. Поле игры. Гипотезы поведения игроков. Построение поля игры на примерах игры «Государство-Предприниматели» и модели контроля с двумя ЛПР.
2.3.1. Поле игры. Гипотезы поведения игроков
Понятие «Поле игры» отражает
игровое содержание множества совместных
выигрышей игроков. Для игры (2.10), (2.11) это
множество (обозначим его
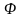 )
определим так:
)
определим так:
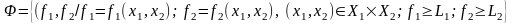 . (2.17)
. (2.17)
Для игроков, которые минимизируют свои выигрыши (например, в игре «Система контроля») их Поле игры определяется выражением, аналогичным (2.17), в котором неравенства с гарантированными результатами заменены на противоположные.
Гипотезы поведения игроков в игре (2.10), (2.11) включает два условия:
1. Оптимальные выигрыши игроков
лежат на «верхней» границе
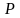 множества
множества
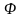 .
Множество
.
Множество
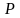 в теории игр носит название множество
парето-оптимальных выигрышей.
Содержательно, это множество таких
выигрышей игроков, что увеличение
выигрыша одного игрока возможно только
при уменьшении (строгом) выигрыша другого
игрока.
в теории игр носит название множество
парето-оптимальных выигрышей.
Содержательно, это множество таких
выигрышей игроков, что увеличение
выигрыша одного игрока возможно только
при уменьшении (строгом) выигрыша другого
игрока.
2. Игроки вправе в процессе
переговоров выбрать оптимальные
стратегии
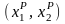 (называют парето-оптимальные стратегии),
соответствующие выигрыши игроков при
которых принадлежат множеству
(называют парето-оптимальные стратегии),
соответствующие выигрыши игроков при
которых принадлежат множеству
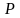 (называют парето-оптимальные выигрыши).
Этот выбор является решением игры, если
выполнено условие обязующего соглашения.
(называют парето-оптимальные выигрыши).
Этот выбор является решением игры, если
выполнено условие обязующего соглашения.
2.3.2. Построение поля игры на примерах игры «Государство-Предприниматели» и модели контроля с двумя ЛПР.
Построение поля игры
«Государство-Предприниматели» состоит
в вычислении параметров выражения
(2.17) используя задание игры (2.7), (2.8).
Непосредственными вычислениями находим:
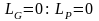 .
Найдем максимальный выигрыш Предпринимателей
.
Найдем максимальный выигрыш Предпринимателей
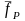 :
:
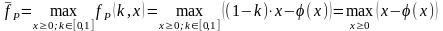 . (2.18)
. (2.18)
Для любого
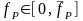 найдем максимальное значение выигрыша
первого игрока:
найдем максимальное значение выигрыша
первого игрока:
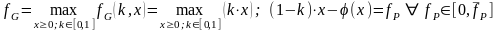 . (2.19)
. (2.19)
Упражнение. Покажите, что
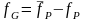 – решение задачи (2.19).
– решение задачи (2.19).
Окончательно получим Поле игры «Государство-Предприниматели» в следующем виде:
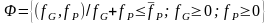 . (2.20)
. (2.20)
Запишем множество парето-оптимальных выигрышей рассматриваемой игры:
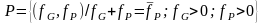 . (2.21)
. (2.21)
Упражнение. Графически
представьте множества
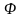 и
и
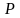 .
.
Задание к вопросу экзамена
2.3.2. Найти множества
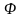 и
и
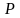 игры «Система контроля» (2.5), (2.6) и
исследовать их свойства. Описать
содержательно интересы игроков, множества
их стратегий. С использованием компьютерных
программ в среде Excel
провести исследование оптимальных
стратегий игроков (минимакс, ситуации
равновесия по Нэшу, по Штакельбергу и
Парето-оптимум). Индивидуальное задание
в МОДУЛ.
игры «Система контроля» (2.5), (2.6) и
исследовать их свойства. Описать
содержательно интересы игроков, множества
их стратегий. С использованием компьютерных
программ в среде Excel
провести исследование оптимальных
стратегий игроков (минимакс, ситуации
равновесия по Нэшу, по Штакельбергу и
Парето-оптимум). Индивидуальное задание
в МОДУЛ.
Раздел 3. Прикладные модели принятия решений: примеры
Модель поведения работника на рабочем месте. Модель оптимизации бонуса менеджеров производственных и финансовых компаний. Математическая модель планирования объединения промышленных предприятий. Имитационная модель планирования объединения промышленных предприятий.

Тема 3.1. Оптимизация бонуса менеджеров производственной и финансовой компаний.
3.1.1. Модель поведения работника на рабочем месте
Приведем основные определения18. Справедливой (рыночно равновесной) будем считать сделку, при которой согласованная заработная плата равна произведению количества продаваемого труда на его цену (сдельная система оплаты труда).
В качестве меры труда (единицы измерения объема работы) выберем часовую норму труда (ЧНТ) – объем работы, который реально выполняет среднерыночный (для сегмента локального рынка) работник в течение одного рабочего часа. Эта характеристика для среднерыночного работника может быть оценена как часовая норма выработки. Такой работник за 8-часовой рабочий день выполнит объем работы 8 ЧНТ. При оплате труда в 100 руб. за ЧНТ его месячная заработная плата (20 рабочих дней) равна 16 000 руб.
Потенциал трудовой активности (ПТА) работника определим, как объем работы в ЧНТ, который он способен выполнить в среднем за рабочий день. Мы также используем понятие фактическая трудовая активность (ФТА) работника.
Приведем пример аналитического выражения для ФТА:
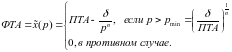 (3.1)
(3.1)
Здесь
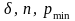 – параметры, значения которых определяются
состоянием локального рынка труда по
заданной профессии работника и его
трудовыми характеристиками.
– параметры, значения которых определяются
состоянием локального рынка труда по
заданной профессии работника и его
трудовыми характеристиками.
Справочно: Смотри глоссарий (Приложение 2) пп. 1, 4, 29, 33, 41, 44.
3.1.2. Модель оптимизации бонуса менеджеров производственных и финансовых компаний
Эффективным механизмом
стимулирования менеджеров является
выделение доли
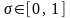 ,
дополнительной прибыли, полученной
этим менеджером, в качестве бонуса
(премиального вознаграждения). Тогда
оптимальное значение
,
дополнительной прибыли, полученной
этим менеджером, в качестве бонуса
(премиального вознаграждения). Тогда
оптимальное значение
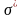 должно обеспечивать максимальные
результаты для собственника рассматриваемой
экономической системы.
должно обеспечивать максимальные
результаты для собственника рассматриваемой
экономической системы.
Рассмотрим задачу оптимизации
бонуса менеджеру, зависимость
среднедневного объема работ которого
от ставки оплаты труда
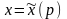 задана выражением (3.1).
задана выражением (3.1).
Обозначим через
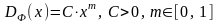 , (3.2)
, (3.2)
зависимость среднедневной валовой прибыли фирмы, полученной за счет активности стимулируемых менеджеров. Функцию (3.2) дополнительной прибыли от трудового вклада менеджера можно получить на основе функции Кобба-Дугласа при постоянной величине капитала фирмы.
Дополнительная валовая
прибыль
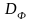 разделяется на чистую прибыль собственника
разделяется на чистую прибыль собственника
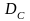 и оплату труда менеджеров
и оплату труда менеджеров
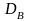 :
:
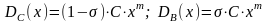 (3.3)
(3.3)
С учетом выражения (3.3) задачу
выбора оптимального значения
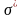 запишем в следующем виде. Найти
запишем в следующем виде. Найти
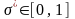 ,
при котором доход собственника является
максимальным:
,
при котором доход собственника является
максимальным:
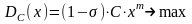 . (3.4)
. (3.4)
Можно показать, что при
фиксированной величине
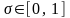 и заданной активности
и заданной активности
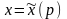 оплата
оплата
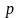 единицы активности и уровень активности
единицы активности и уровень активности
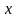 определятся из следующего уравнения:
определятся из следующего уравнения:
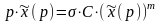 ,
(3.5)
,
(3.5)
решение которого необходимо учитывать как дополнительное условие задачи (3.4).
В описании к лабораторной работе 4 представлена методика идентификации функции (4.5) и программное обеспечение в среде Excel для решения задачи (4.7) в случае, когда в (4.1) параметр n равен единице.
Задание по теме 3.1.2. Выполнить расчетную работу по оптимизации бонуса менеджера для индивидуальных исходных данных, представленных в МОДУЛ.
Справочно: Смотри глоссарий (Приложение 2) пп. 3.2, 3.12, 1.24.
Тема 3.2. Математические модели планирования производства на основе математического программирования.
3.2.1. Математическая модель планирования объединения предприятий.
В сложных системах (с двумя и более центрами принятия решений) кроме основных функций управления возникают дополнительные, такие как согласование и координация решений. Координация решения – это согласование деятельности, целей, зон ответственности, распределение общих ресурсов, совместного дохода.
Типичным примером сложной системы в экономике является система корпоративного управления – организационная модель, с помощью которой корпорация представляет и защищает интересы своих инвесторов. Тип применяемой модели зависит от структуры корпорации, существующей в рамках рыночной экономики, и отражает факт разделения функций владения и управления корпорацией. В общем случае, корпорация – объединение n юридических лиц плюс одна управляющая компания, которую далее называем Центром.
Исследование проводится на примере задачи квадратичного программирования, которая рассматривается как математическая модель планирования объединения Т промышленных предприятий в следующем виде19:
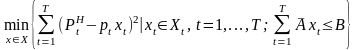 , (3.6)
, (3.6)
где
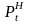 – потенциальная прибыль, а
– потенциальная прибыль, а
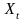 – допустимое множество планов предприятия
– допустимое множество планов предприятия
 в составе корпорации:
в составе корпорации:
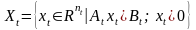 .
.
Матрицы в приведенных
выражениях имеют следующие размерности:
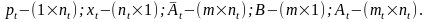
Экономический смысл модели планирования состоит в оптимизации планов производства объединения, при котором потенциальные возможности предприятий по прибыли максимально реализуются при ограниченных ресурсах объединения.
Справочно: глоссарий (Приложение 2) пп. 3.4 – 3.6.
3.2.2. Имитационная модель планирования объединения промышленных предприятий
Имитационная модель разработана
в среде Excel для исследования
проблемы планирования объединения
промышленных предприятий. Для генерации
матриц в условиях задачи (3.6) задаются
их размерности, а значения элементов
матриц заполняются равномерно
распределенными псевдо случайными
числами в заданных интервалах. Значения
параметров
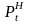 для
каждого предприятия определяются
решением задач линейного программирования
при условии выделения предприятию
для
каждого предприятия определяются
решением задач линейного программирования
при условии выделения предприятию
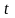 всего объема имеющихся ресурсов
объединения. Индивидуальные варианты
исходных данных задаются своим списком
5 предприятий для объединения.
всего объема имеющихся ресурсов
объединения. Индивидуальные варианты
исходных данных задаются своим списком
5 предприятий для объединения.
Таким образом, в процессе исследования задачи планирования решаются 5 задач линейного программирования и одна задача квадратичного программирования (3.6).
Задание по теме 3.2.2. Провести исследование задачи планирования объединения предприятий для индивидуальных исходных данных, приведенных в МОДУЛ.