Файл: Математические модели принятия решений - УЧЕБНЫЕ МАТ-2018.docx
Добавлен: 29.10.2018
Просмотров: 3002
Скачиваний: 29
СОДЕРЖАНИЕ
Тема 1.1. Классификация и принципы. Моделирование процессов и решений.
1.1.1. Основные понятия теории принятия решений. Историческая справка.
1.1.2. Технология решения прикладных задач поддержки принятия решений.
1.1.3. Место исследования операций в математическом моделировании.
1.1.5. Понятие математической модели принятия решений
1.1.6. Моделирование процессов
1.2.1. Производственные функции
1.2.2. Задача оптимального среднесрочного плана развития производства
Тема 1.3. Математические модели поддержки принятия решений в условиях риска и неопределенности.
1.3.1. Принципы обоснования решений в условиях риска и неопределенности.
1.3.2. Портфельный анализ: модель Марковица.
1.3.3. Инструментальные средства портфельного анализа
2.1.1. Модель контроля с одним ЛПР
2.1.2. Модель выборочного контроля с одним ЛПР
2.1.3. Модель контроля с двумя ЛПР
2.1.4. Игра «Государство-Предприниматели»
2.2.1. Минимаксные стратегии: игра двух лиц
2.2.2. Ситуации равновесия по Нэшу и Штакельбергу: игра двух лиц
2.3.1. Поле игры. Гипотезы поведения игроков
Раздел 3. Прикладные модели принятия решений: примеры
Тема 3.1. Оптимизация бонуса менеджеров производственной и финансовой компаний.
3.1.1. Модель поведения работника на рабочем месте
3.1.2. Модель оптимизации бонуса менеджеров производственных и финансовых компаний
3.2.1. Математическая модель планирования объединения предприятий.
3.2.2. Имитационная модель планирования объединения промышленных предприятий
Методы математического моделирования не являются универсальными и представляют особые требования к исследуемой проблемной ситуации. Наиболее существенными из них является нетривиальность решаемой проблемы и ее начальная структурированность.
Простые проблемы с незначительными ущербами лучше решать интуитивно на основе «здравого смысла».
Требование структурированности проблемы является более сложным, связанным со специальной обработкой проблемной области, выявлением главных факторов и существенных связей.
Характерным примером гениальной
структурированности является формулировка
закона всемирного тяготения, в
математическом отражении которого
используется две материальные точки
массой
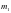 и
и
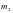 находящиеся на расстоянии
находящиеся на расстоянии
 .
.
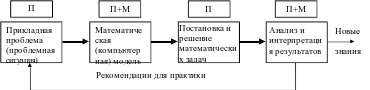
Рис. 1.1. Процесс решения проблемы с использованием математической (компьютерной) модели:
П – этапы аналитического исследования, функционально выполняемые предметными специалистами, в зависимости от предметной области; М – этапы аналитического исследования, функционально выполняемые математиками; П+М – этапы, выполняемые предметниками и математиками совместно.
Модель записана предельно
просто. Сила сближения тел определена
так:
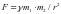 .
.
В работе1 приведены примеры из произведений А.С. Пушкина проблемных ситуаций, которые в описании идеально подготовлены для их математического моделирования.
Другим аспектом рассматриваемой технологии является абстрактность получаемых результатов. На примере закона всемирного тяготения видно, что в чистом виде реально моделируемой системы не существует, однако теоретическое и прикладное значение этого закона трудно переоценить. По этому поводу можно привести слова А.С. Пушкина: «Сказка ложь, но в ней намек! Добрым молодцам урок». В нашем контексте сказка это – непосредственный результат, который следует из математической модели. На практике математику и предметному специалисту следует наполнить его предметным содержанием и творчески применить для решения рассматриваемой проблемы. Модель и результаты ее исследования выполняют функции знаковой системы. Исследователь, используя ассоциативные знания, формирует целостный образ требуемой реальной системы2.
Справочно: Смотри глоссарий (Приложение 2) пп. 1.4, 1.10, 1.12.
1.1.3. Место исследования операций в математическом моделировании.
Исторически заметные и значимые применения математических методов в прикладных областях возникли параллельно с освоением ЭВМ, т.е. в 50-60 годах прошлого века. В научной литературе практика применения математических методов оформилась в рамках исследования операций3
Задание к вопросу экзамена 1.1.3. Ответить на вопросы 1-40 теста, приведенного в файле «ТЕСТ - начало исследования операций.pdf» (файл прилагается в МОДУЛ).
Справочно: Смотри глоссарий (Приложение 2) пп. 1.6, 1.7, 1.23.
1.1.4. Классификация математических моделей по типу математических задач и по свойствам предметной области
В теории экономико-математического моделирования выделяют 2 основных класса математических моделей (модели процессов и модели решений), используемых в трех типах исследовательских задач: оценка параметров экономических процессов и систем; прогнозирование временных рядов и событий; обоснование оптимальных решений.
Эти задачи можно выразить формулой активных действий: «знать», «предвидеть», «управлять». Отмеченная классификация математических моделей представлена на рисунке 1.2.
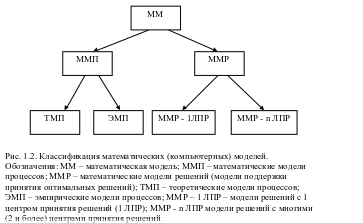
Полезно пользоваться определением математических (компьютерных) моделей.
ММ это отражение в математических символах или в компьютерных операторах существенных сторон исследуемого явления или процесса.
Существует строгое различие математических и компьютерных моделей. Свойства математических моделей и получаемые с их использованием результатов исследуются строгим математическим аппаратом (методами). Компьютерные модели исследуются на ЭВМ.
Справочно: Смотри глоссарий (Приложение 2) пп. 1.2, 1.5, 1.12, 1.13, 3.8.
1.1.5. Понятие математической модели принятия решений
В данном месте следует пояснить объект моделирования, учитывая, что модель – отражение реальности. Конечным результатом модельных расчетов, является вариант решения, который предлагает аналитик. Но аналитик не несет ответственности за последствия принимаемого решения (кроме особых процедур страхования профессиональной ответственности). Кроме того, заказчик может дать задание аналитику предсказать решение конкурента в конкретной экономической ситуации.
В теории экономико-математического моделирования принято считать объектом моделирования лицо, принимающее решение (ЛПР). ЛПР – обобщенное и абстрактное понятие, в которое включено совокупность свойств реальных центров принятия решений, условий (экономических, финансовых, информационных, временных) в которых это решение формируется, границы зон ответственности решений, возможности (или невозможности) их корректирования и т.д. Реально решения могут приниматься с разной степенью рациональности в стандартных или в уникальных ситуациях.
В экономической литературе наиболее простым и часто используемым образом ЛПР выступает экономический человек4. Этим свойством наделяют субъектов экономической деятельности: не только отдельных людей, но и руководство предприятий, корпораций, органов государственного, местного самоуправления и стран в целом.
Модели решений с 1 ЛПР.
В простом случае считается,
что ЛПР знает список возможных решений
(математически множество
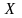 ),
полезность каждого решения (математически
функция
),
полезность каждого решения (математически
функция
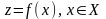 )
и выбирает оптимальное решение
)
и выбирает оптимальное решение
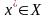 ,
которое имеет максимальную полезность.
,
которое имеет максимальную полезность.
Математически модель решений
(1 ЛПР) записывается так: найти
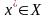 из условий5:
из условий5:
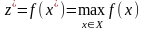 . (1.1)
. (1.1)
В этом выражении
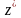 или
или
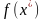 – значение оптимальной (максимальной)
полезности.
– значение оптимальной (максимальной)
полезности.
Задание 1 к вопросу экзамена 1.1.5. Пример задачи обоснования оптимального решения по проблеме «Затон в г. Барнаул. Исходные данные приведены в МОДУЛ.
Модели решений с n ЛПР (модели теории игр).
На рисунке 1.2 выделены
математические модели решений с n
ЛПР (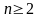 ),
которые используются для исследования
экономических систем с многими центрами
принятия решений. На практике трудно
разделить системы с одним и многими
центрами принятия решений. Но характерными
примерами систем с n ЛПР
выступают системы: «работник-работодатель»,
«контрольный орган-исполнитель»,
«товарный или финансовый рынки в условиях
конкуренции», «корпоративное управление»6.
),
которые используются для исследования
экономических систем с многими центрами
принятия решений. На практике трудно
разделить системы с одним и многими
центрами принятия решений. Но характерными
примерами систем с n ЛПР
выступают системы: «работник-работодатель»,
«контрольный орган-исполнитель»,
«товарный или финансовый рынки в условиях
конкуренции», «корпоративное управление»6.
Задачей при исследовании этих систем выступает построение математической (компьютерной) модели, с использованием которой можно предсказать решения всех ЛПР. Классической работой в данной области является книга Дж. фон Неймана и О. Моргенштерна, которая написана в США в 1944 г. На русском языке книга стала известной с 1970 г.7
Основные принципы математического моделирования экономических процессов и систем сохраняются и в рассматриваемой области. Дополнительными задачами выступают обоснование уровня знаний всех ЛПР объекта моделирования о своих списках решений, целевых функциях, порядках ходов, об уровнях взаимной информированности и принятых правилах совестного выбора и реализации решений. Трудности математического моделирования связаны с наличием неполной информации об условиях выбора решений и о решениях, принимаемых другими ЛПР8.
Многокритериальные модели решений с 1 ЛПР
Рассматриваем модели решений
с одним ЛПР, которое оценивает полезность
решений вектором показателей. Например
эффект инвестиций определяется их
доходностью и уровнем риска. При выборе
варианта решения необходимо найти
компромисс между этими критериями. В
общем случае на множестве решений
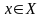 могут быть заданы n
(
могут быть заданы n
(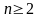 )
целевых показателей, часть которых
требуется минимизировать, а часть –
максимизировать. Без потери общности
можно считать, что все критерии следует
максимизировать9.
В теории экономико-математического
моделирования используют 2 подхода:
)
целевых показателей, часть которых
требуется минимизировать, а часть –
максимизировать. Без потери общности
можно считать, что все критерии следует
максимизировать9.
В теории экономико-математического
моделирования используют 2 подхода:
1. Свертка критериев, т.е. сведение многокритериальной задачи к однокритериальной задаче обоснования решений. Используют линейные и специальные нелинейные функции свертки частных критериев.
2. Выбор одного критерия в качестве ведущего и введение ограничений на уровни снижения значений по всем другим критериям.
Пример. Пусть задана
задача принятия решений с n
(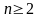 )
критериями
)
критериями
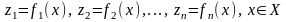 .
Введем интегральный критерий
.
Введем интегральный критерий
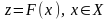 :
:
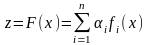 ,
где
,
где
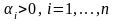 – заданные «веса» частных критериев.
Тогда многокритериальная модель решения
сводится к модели (1.1) с целевой функцией
– заданные «веса» частных критериев.
Тогда многокритериальная модель решения
сводится к модели (1.1) с целевой функцией
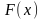 .
.
Упражнение. Исследовать модель Марковица поиска оптимального инвестиционного портфеля, заданной ниже выражениями (1.23) – (1.25). Показать, что данная модель является двухкритериальной, а для поиска решения выбран подход 2, т.е. выбран ведущий критерий (какой?), а второй критерий (какой?) ограничен по значению.
Модели решений с 1 ЛПР в условиях природной неопределенности
В настоящее время разработаны варианты математических моделей решений (1 ЛПР) в условиях ограниченной информированности (ЛПР не знает полного списка решений, ЛПР неточно оценивает полезности решений, информированность аналитика не совпадает с информированностью ЛПР). Основные подходы к построению таких моделей связаны с использованием теории вероятностей (модели решений в условиях риска) и интервального (теоретико множественного) анализа (модели решений в условиях неопределенности10).
Общий вид математической модели в условиях неопределенности (не полной информированности ЛПР) задается следующими выражениями11:
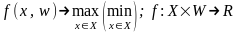 . (1.2)
. (1.2)
В выражении (1.2) функция
полезности является скалярной (в простом
случае многокритериальность не
рассматривается), множества
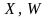 – множество решений ЛПР и множество
неконтролируемых параметров
– множество решений ЛПР и множество
неконтролируемых параметров
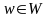 – считаются известными аналитику и
ЛПР. Следует отметить, что выражения
(1.1) и (1.2), как модели поддержки принятия
решения, существенно различны. Модель
(1.1) является математической задачей
оптимизации (линейное, нелинейное
программирование, вариационного
исчисления и др.). Для поиска оптимального
решения согласно (1.2) необходима редукция
этого выражения к математической задаче.
Для этой редукции необходима математическая
модель неконтролируемого параметра и
модель отношения ЛПР к риску. Эти вопросы
подробнее рассмотрим в разделе 1.3.
– считаются известными аналитику и
ЛПР. Следует отметить, что выражения
(1.1) и (1.2), как модели поддержки принятия
решения, существенно различны. Модель
(1.1) является математической задачей
оптимизации (линейное, нелинейное
программирование, вариационного
исчисления и др.). Для поиска оптимального
решения согласно (1.2) необходима редукция
этого выражения к математической задаче.
Для этой редукции необходима математическая
модель неконтролируемого параметра и
модель отношения ЛПР к риску. Эти вопросы
подробнее рассмотрим в разделе 1.3.
Задание 2 к вопросу экзамена 1.1.5. Рассмотреть примеры моделей обоснования решений в условиях неопределенности (задание в МОДУЛ).
Справочно: Смотри глоссарий (Приложение 2) пп. 1.7, 1.11, 1.14, 1.21.