Добавлен: 19.10.2018
Просмотров: 3427
Скачиваний: 9

36
Средство Поиск решения активируется в меню Сервис (если это средство не
установлено, то это необходимо сделать).
Предварительно проводят следующую подготовительную работу.
Отводят для каждой переменной по ячейке.
Вводят формулы для вычисления правых частей уравнений системы (по одной
формуле в ячейку).
После этого запускают Поиск решения. Возможный вид экрана для подготовки
к решению той же системы, что и выше, приведен на рис.
Рис.2
На этом рисунке под переменные отведены ячейки A2:D2, под формулы —
ячейки А4, А6, А8 и А10. Какие именно числовые значения переменных будут
введены в ячейки A2:D2, при решении системы линейных уравнений значения не
имеет (итерационная процедура, заложенная в Поиск решения, стартует с этих
значений).
Еще один элемент в таблице — целевая функция. Она в данном случае особой
роли не играет, но какую-нибудь формулу ввести необходимо, иначе Поиск
решения работать не может (напомним, что эта программа нацелена на другой
класс задач). Точно так же неважно, как установлен флажок: «максимальному
значению» или «минимальному значению».
Теперь необходимо ввести то, что в форме на рис. 2 именуется ограничениями.
Щелкнув по кнопке Добавить, получают другую форму (рис.3 ).
Рис3.
В форму, изображенную на рис. 3. надо ввести четыре условия (по числу
уравнений системы). На рисунке отражено последнее условие. Ссылка на ячейку
А10 обусловлена тем, что в ней -формула для левой части 4-го уравнения, знак '='
выбран из меню, число (-13) введено с клавиатуры (правая часть 4-го уравнения).
После ввода последнего ограничения нажимают кнопку ОК и возвращаются в

37
основную форму Поиск решения. Щелкнув по кнопке Выполнить, получают
результат (рис. 4).
Рис4.
Каким методом это решение получено, можно узнать, щелкнув по кнопке
Параметры (см. рис. 2). Там, в частности, есть знакомый нам метод Ньютона
(наверняка сильно видоизмененный, поскольку применяется на самом деле к
решению гораздо более сложной задачи).
Поиск решения можно попытаться применить и к решению систем нелинейных
уравнений. В этом случае выбор начального приближения очень важен, в
зависимости от него решение может быть получено или не получено и могут
быть получены разные решения.
Контрольные вопросы и задания
1) Запустить программу Excel, открыть рабочую книгу лабораторных работ.
Создать в ней новый лист, дать ему имя «Мет.итераций».
2) Оформить рабочий лист.
Значения коэффициентов матрицы P и вектора b взять по своему варианту,
таблица 4 Приложения.
3) Привести систему к виду (4).
4) Умножить матрицу P и вектор b на транспонированную матрицу P
T
Преобразовать коэффициенты по формулам (4'). В формулах вычисления
коэффициентов a
ij
и b
i
(i
≠ j) использовать абсолютную адресацию.
Коэффициенты a
ii
задать равными нулю.
5) Для начала итерационного процесса задать значение вектора x
0
равным b.
Ввести формулы для вычисления x
k+1
и d. При ссылке на матрицу А можно
использовать абсолютные адреса, для вектора b удобно ячейкам с элементами
вектора присвоить имена и в формулах ссылаться на них:
Ячейкам со значениями величин ε и d также следует присвоить имена для
использования в формулах.

38
Для переноса значений x
k+1
на следующий шаг в ячейки x
k
необходимо
использовать функцию ЕСЛИ с условием ε<d.
6) Копировать ячейки, относящиеся к одному шагу итераций до тех пор, пока
ε<d.
7) Выделить в отдельные ячейки окончательный ответ с 3 десятичными
знаками. Сравнить полученные значения с точным решением системы уравнений
и решением, полученным выше.
СЛАУ можно записать в матричном виде
Ax=b
где А – матрица коэффициентов при неизвестных;
х – вектор неизвестных;
b –
вектор свободных членов.
При решении СЛАУ можно использовать метод обратной матрицы. Тогда
решение можно найти по формуле
x=A
-1
⋅
b
Пример. Решить систему линейных алгебраических уравнений (СЛАУ)
=
+
−
=
+
=
+
−
1
12
2
6
6
2
3
4
2
6
3
2
1
3
1
3
2
1
x
x
x
x
x
x
x
x
Для решения СЛАУ методом обратной матрицы необходимо:
1.
Задать матрицу коэффициентов при неизвестных A и вектор свободных членов b.
2.
Проверить детерминант матрицы А.
3.
Если детерминант не равен 0, найти обратную матрицу A
-1
4.
Умножить обратную матрицу на вектор свободных членов.
Решение СЛАУ в системе Scilab.
Специальные матричные функции необходимые для решения СЛАУ методом
обратной матрицы:
-
Функция det(А) вычисляет определитель квадратной матрицы А.
-
Функция inv(A) вычисляет обратную матрицу к матрице А.
Решение СЛАУ с помощью этого метода приведено на рис. 20.

39
Рис. 20. Решение СЛАУ с использованием обратной матрицы
Решить СЛАУ, заданную в виде уравнения
0
=
− b
x
A
используя функцию linsolve(A, b)
можно, (рис. 21).
Рис. 21. Решение СЛАУ с использованием функции linsolve
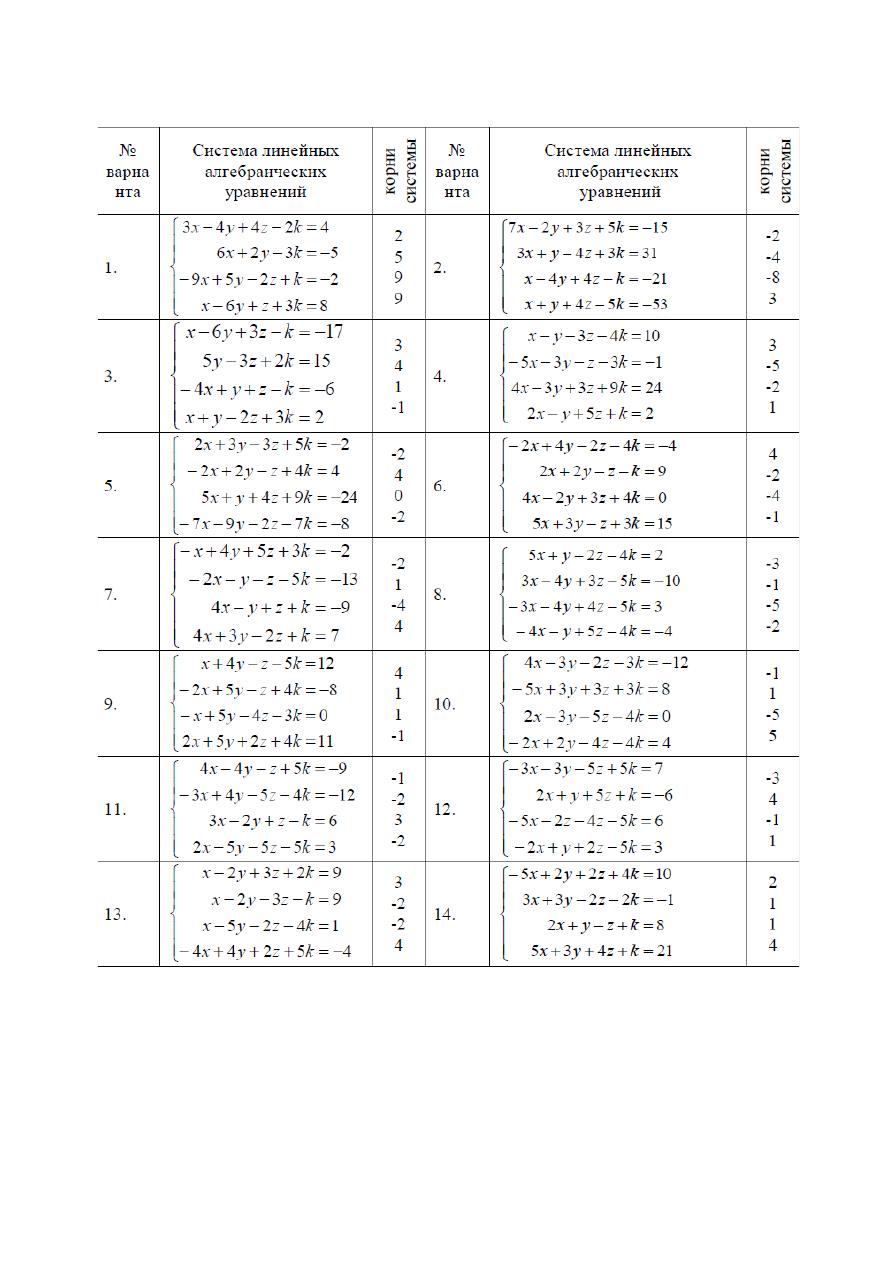
Решите систему методом обратной матрицы.
40
Таблица 4 Варианты СЛАУ