Файл: Методические указания по изучению дисциплины и выполнению контрольных работ для студентов заочной формы обучения направлений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 133
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
означает, что задача решена, то условные вероятности решить задачу при условии, что это задача по пределам, дифференциальному или интегральному исчислению, соответственно равны:
; 
; 
.
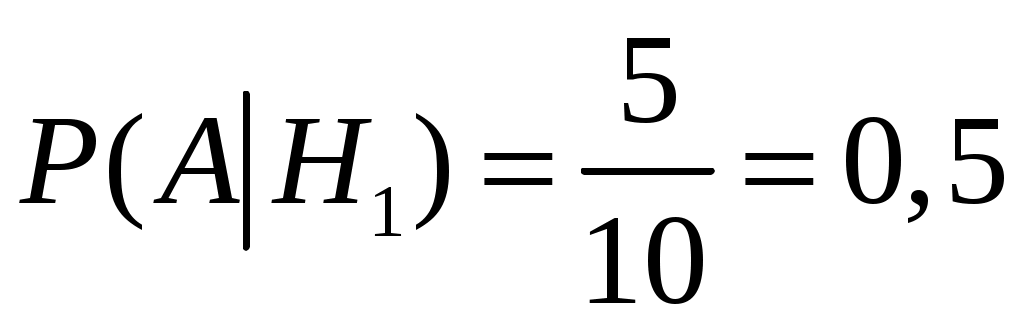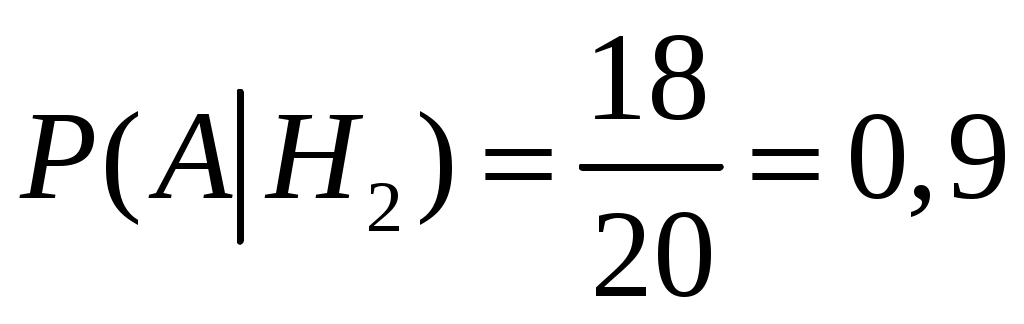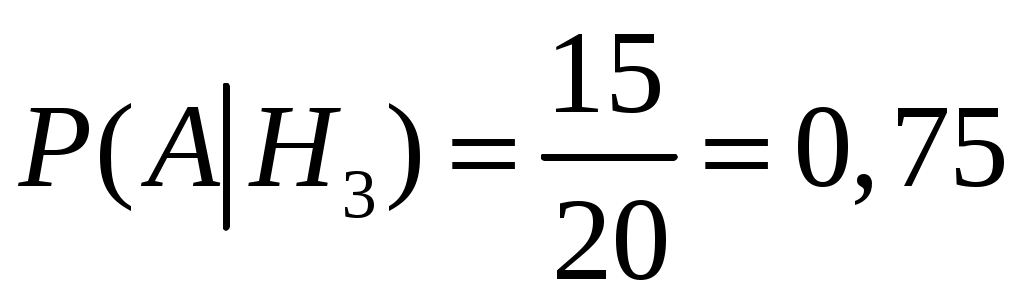События
,
и 
попарно несовместны и одно из них всегда наблюдаемо при любом исходе. Тогда по формулеполной вероятности
находим вероятность сдачи зачета
.
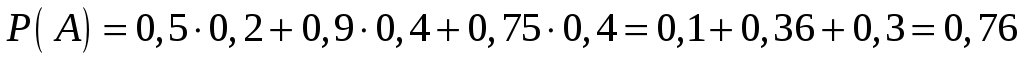Задание №9. Заданы математическое ожидание т и среднее квадратичное отклонение нормально распределенной случайной величины х. Найти:
1) вероятность того, что х примет значение, принадлежащее интервалу (, ).
2) вероятность того, что абсолютная величина отклонения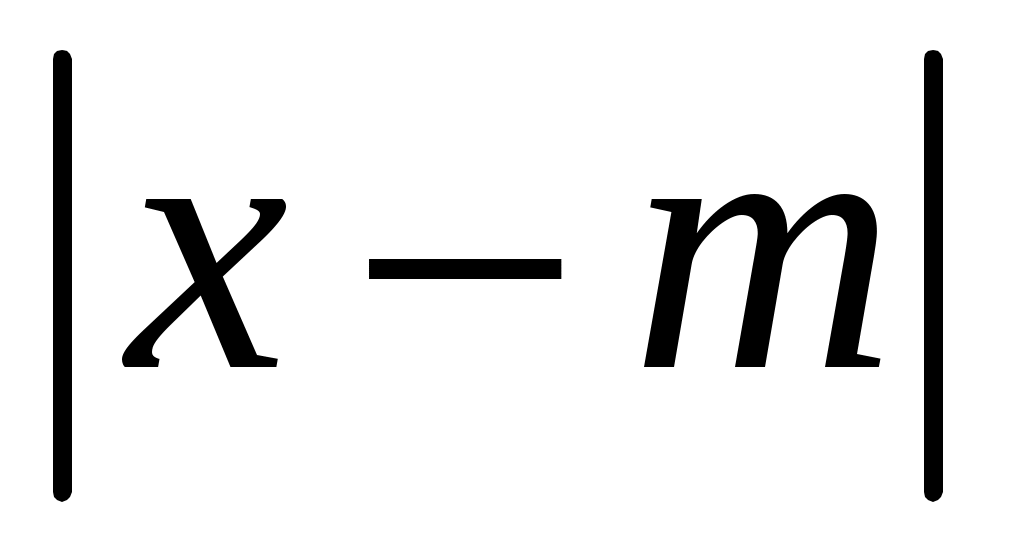
окажется меньше .
Пример. m =15, = 2, =16, = 25, = 4. 1) Воспользуемся формулой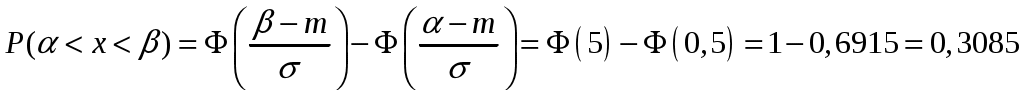
, где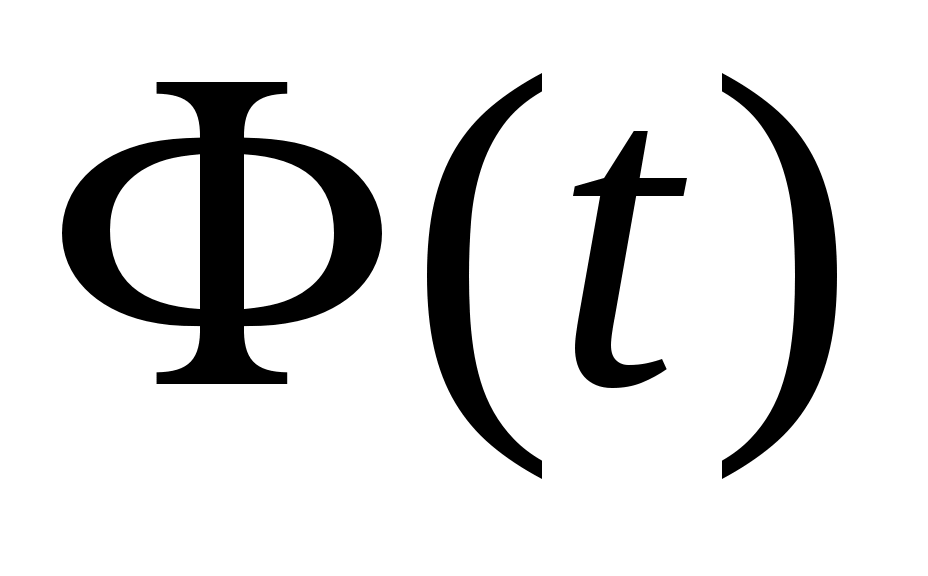 
функция Лапласа: 
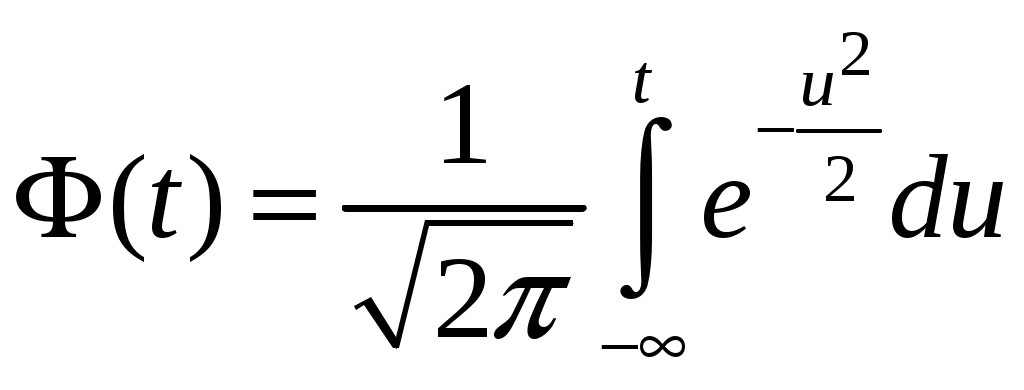. Её значения находим из статистических таблиц.
2) Воспользуемся формулой:
.
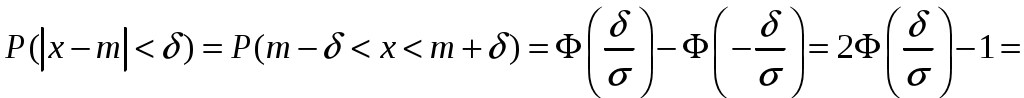
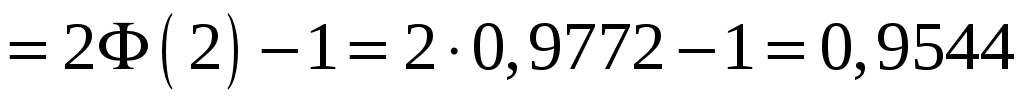Задание №10. Найти выборочное уравнение прямой линии регрессии Y на Х по данным, приведенным в корреляционной таблице.
Пример.
Решение.
Составим корреляционную таблицу в условных вариантах, выбрав в качестве ложных нулей С1=30 и С2= 36 ( каждая из этих вариант расположена в середине соответствующего вариационного ряда).
Найдем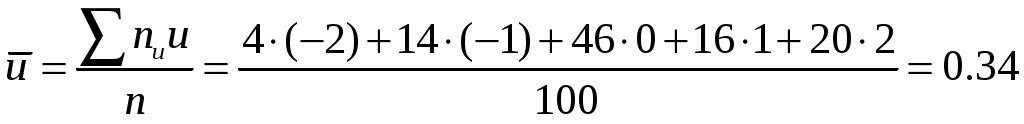
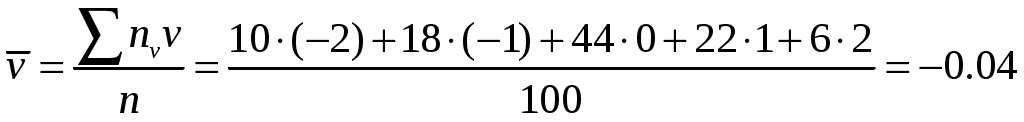
Найдем вспомогательные величины
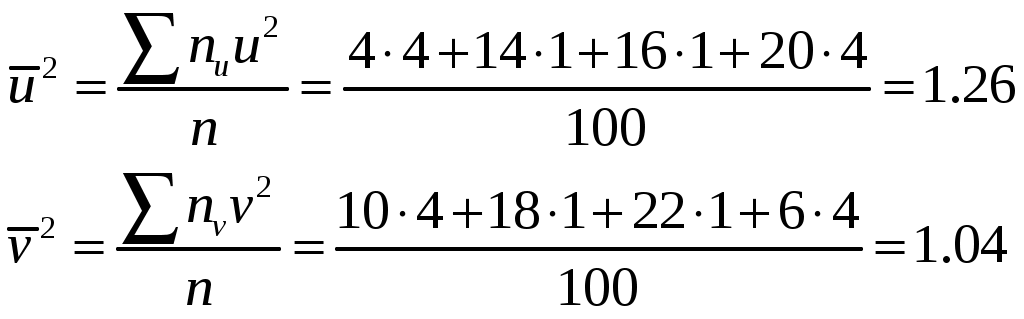
Найдем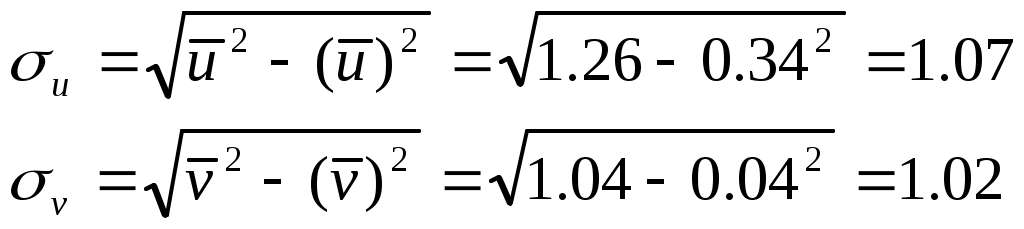
Составим расчетную таблицу.
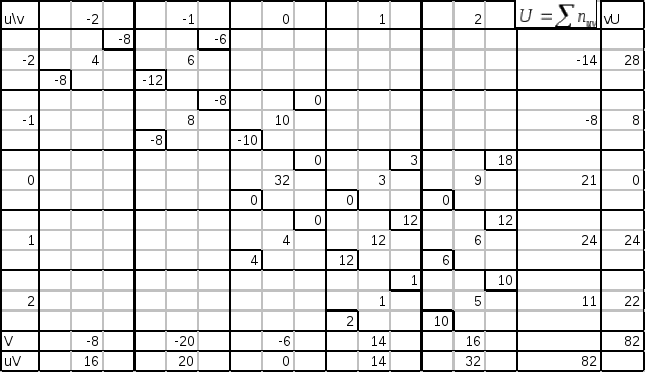
Пояснения к составлению таблицы.
1). Произведение частоты nuv на варианту u записывают в правом верхнем углу клетки, содержащей значение частоты.
2). Складывают все числа, помещенные в правых верхних клеток одной строки, и их сумму помещают в клетку этой же строки «столбца U».
3). Наконец, умножают варианту v на U и полученное произведение записывают в соответствующую клетку « столбца vU».
4). Сложим все числа « столбца vU», получают сумму vU, которая равна искомой сумме
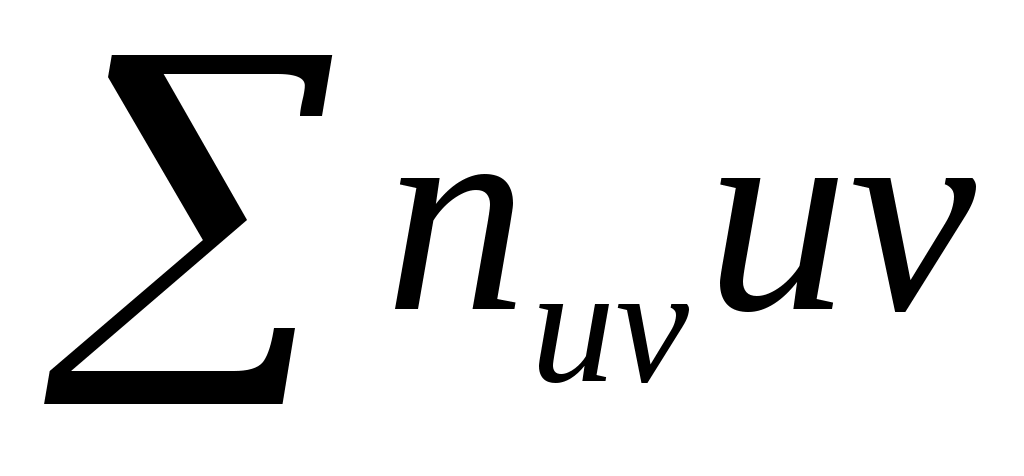. Например, для нашей таблицы искомая сумма 
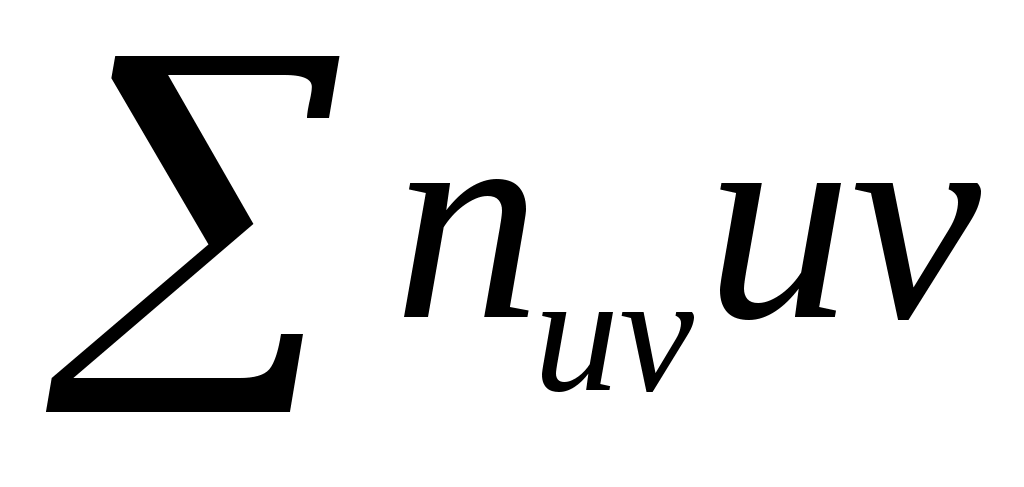=82.
Для контроля аналогичные вычисления производят по столбцам.
Найдем искомый выборочный коэффициент корреляции: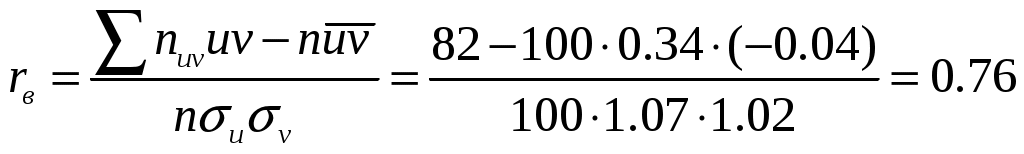
. Найдем шаги h1 и h2 (разности между любыми двумя соседними вариантами): h1=25-20=5; h2=26-16=10/
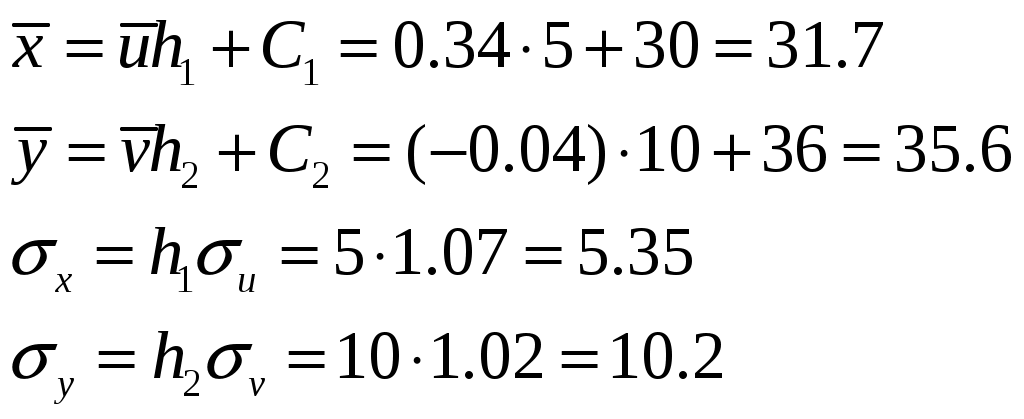
Подставив найденные величины , получим искомое уравнение прямой линии регрессии У на Х:
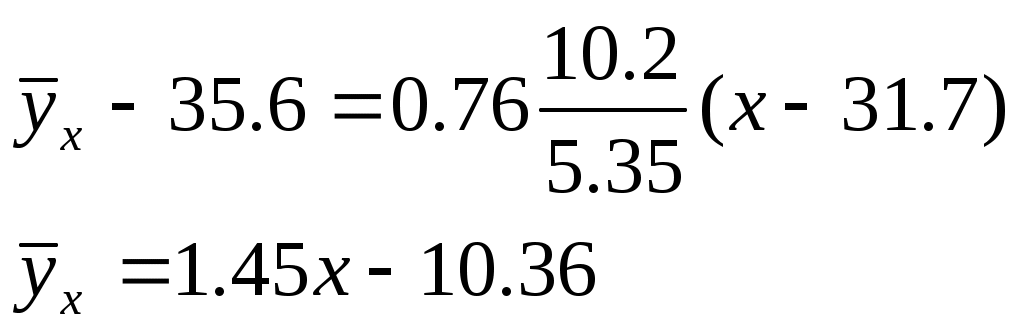
4 Темы практических занятий
4.1 Темы практических занятий. Семестр 1
1. Матрицы и действия над ними. Определители 2-го и 3-го порядка. Обратная матрица и ее нахождение. Решение систем уравнений с помощью обратной матрицы. . Метод Крамера. Метод Гаусса. Теорема Кронекера-Капелли. . Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов. Коллинеарные и компланарные векторы. Разложение вектора по базису i, j, k.
2. Различные формы уравнений прямой на плоскости. Расстояние от точки до прямой. Плоскость в пространстве. Угол между плоскостями. Расстояние от точки до плоскости. Прямая в пространстве. Угол между прямыми. Угол между прямой и плоскостью. Расстояние от точки до прямой.Уравнение прямой, проходящей через две точки, параллельность прямой и плоскости, вычисление углов.
3. Предел функции. Односторонние пределы функции. Непрерывная функция. Точки разрыва и их классификация.Вычисление пределов с использованием 1-го замечательного предела. Сравнение функций. Вычисление пределов с использованием 2-го замечательного предела. Вычисление производных и дифференциалов 1-го порядка. Дифференцирование функций, заданных параметрически. Общая схема исследования функции и построение ее графика.
4. Таблица интегралов. Непосредственное интегрирование. Замена переменной в неопределенном интеграле. Интегрирование по частям в неопределенном интеграле. Интегрирование рациональных дробей. Интегрирование тригонометрических выражений. Интегрирование иррациональных выражений.
4.2 Темы практических занятий. Семестр 2
1. Функции нескольких переменных. Область определения, пределы, непрерывность. Частные производные первого и второго порядков. Экстремумы функции двух переменных.
2. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли. Уравнения старших порядков, допускающие понижение порядка. Линейные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью.
3. Признаки сходимости знакопостоянных рядов. Абсолютно и неабсолютно сходящиеся ряды. Признак сходимости Лейбница. Степенные ряды. Радиус и интервал сходимости. Ряды Тейлора. Вычисление значений функций и интегралов с помощью степенных рядов. Нахождение решений дифференциальных уравнений с помощью степенных рядов.
4. Классическая вероятностная схема. Условные вероятности. Независимость случайных событий. Формула полной вероятности и формула Байеса. Повторные испытания. Формула Бернулли и формула Пуассона. Локальная и интегральная теоремы Лапласа-Муавра. Дискретные и непрерывные случайные величины. Среднее значение и дисперсия. Элементы математической статистики. Выборка и ее представление. Выборочное среднее и выборочная дисперсия. Оценка параметров распределения по выборке.
5 Содержание и оформление контрольных работ
1. Требования к оформлению контрольных работ: контрольные работы могут выполняться на электронных носителях или в тетради (12 л.), на обложке необходимо указать номер контрольной работы, свой факультет, специальность, шифр зачетной книжки, номер варианта, свою фамилию, имя, отчество.
2. Требования к выполнению контрольной работы:
- при выполнении работы необходимо приводить основные математические формулы и промежуточные математические расчёты.
- в конце работы указывается список использованных источников, ставится число и личная подпись.
; ; .События
, и попарно несовместны и одно из них всегда наблюдаемо при любом исходе. Тогда по формулеполной вероятности находим вероятность сдачи зачета
.Задание №9. Заданы математическое ожидание т и среднее квадратичное отклонение нормально распределенной случайной величины х. Найти:
1) вероятность того, что х примет значение, принадлежащее интервалу (, ).
2) вероятность того, что абсолютная величина отклонения
окажется меньше .Пример. m =15, = 2, =16, = 25, = 4. 1) Воспользуемся формулой
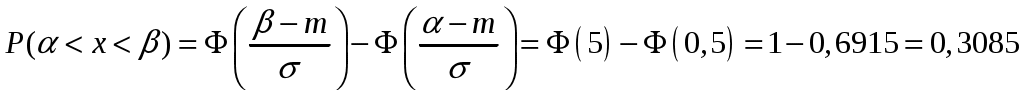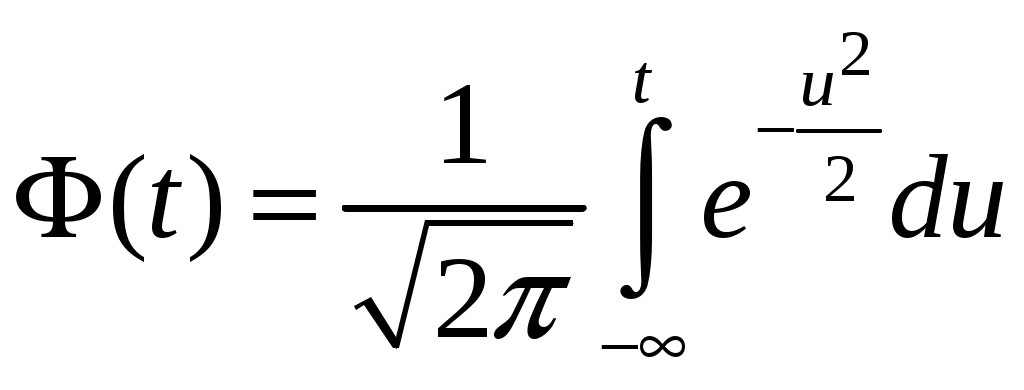, где функция Лапласа: . Её значения находим из статистических таблиц.2) Воспользуемся формулой:
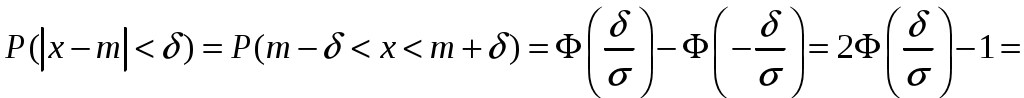
.Задание №10. Найти выборочное уравнение прямой линии регрессии Y на Х по данным, приведенным в корреляционной таблице.
Пример.
| Y | X | ny | ||||
| 20 | 25 | 30 | 35 | 40 | ||
| 16 | 4 | 6 | | | | 10 |
| 26 | | 8 | 10 | | | 18 |
| 36 | | | 32 | 3 | 9 | 44 |
| 46 | | | 4 | 12 | 6 | 22 |
| 56 | | | | 1 | 5 | 6 |
| nx | 4 | 14 | 46 | 16 | 20 | N=100 |
Решение.
Составим корреляционную таблицу в условных вариантах, выбрав в качестве ложных нулей С1=30 и С2= 36 ( каждая из этих вариант расположена в середине соответствующего вариационного ряда).
| v | u | nv | ||||
| -2 | -1 | 0 | 1 | 2 | ||
| -2 | 4 | 6 | | | | 10 |
| -1 | | 8 | 10 | | | 18 |
| 0 | | | 32 | 3 | 9 | 44 |
| 1 | | | 4 | 12 | 6 | 22 |
| 2 | | | | 1 | 5 | 6 |
| nu | 4 | 14 | 46 | 16 | 20 | N=100 |
Найдем
Найдем вспомогательные величины
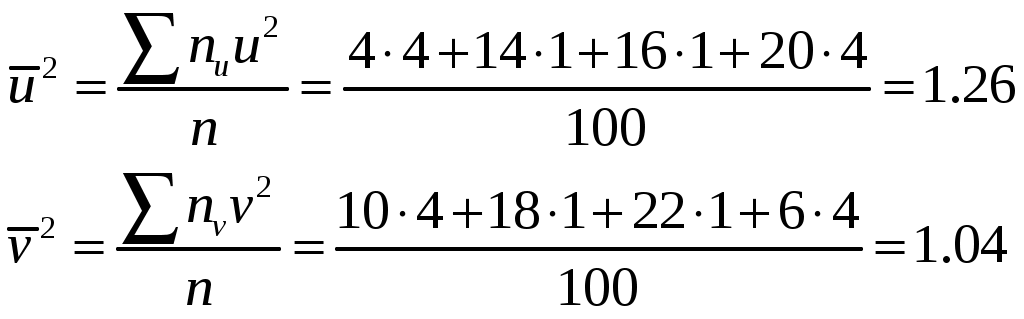
Найдем
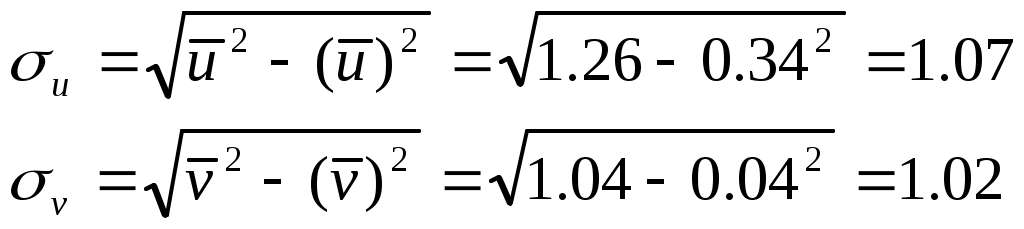
Составим расчетную таблицу.
Пояснения к составлению таблицы.
1). Произведение частоты nuv на варианту u записывают в правом верхнем углу клетки, содержащей значение частоты.
2). Складывают все числа, помещенные в правых верхних клеток одной строки, и их сумму помещают в клетку этой же строки «столбца U».
3). Наконец, умножают варианту v на U и полученное произведение записывают в соответствующую клетку « столбца vU».
4). Сложим все числа « столбца vU», получают сумму vU, которая равна искомой сумме
. Например, для нашей таблицы искомая сумма =82.Для контроля аналогичные вычисления производят по столбцам.
Найдем искомый выборочный коэффициент корреляции:
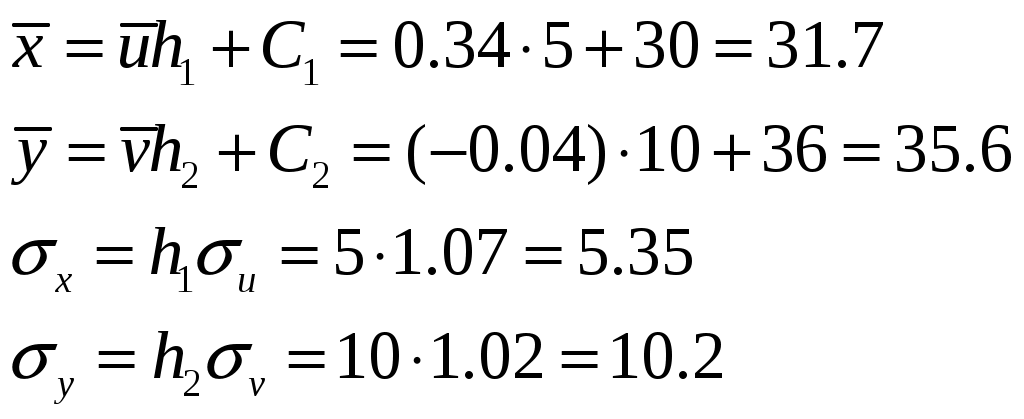
. Найдем шаги h1 и h2 (разности между любыми двумя соседними вариантами): h1=25-20=5; h2=26-16=10/ Подставив найденные величины , получим искомое уравнение прямой линии регрессии У на Х:
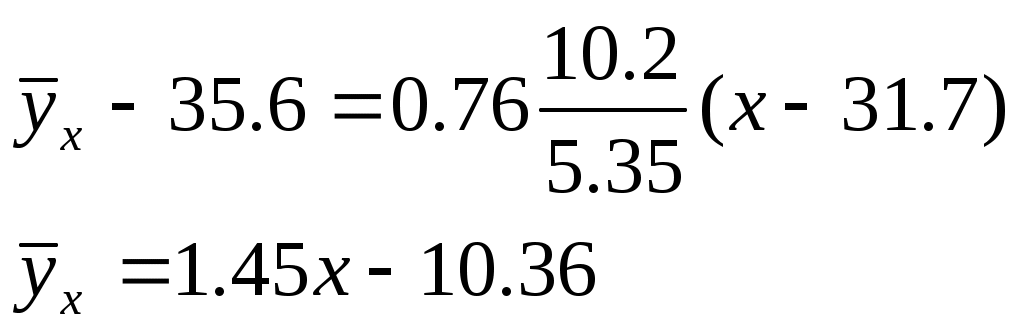
4 Темы практических занятий
4.1 Темы практических занятий. Семестр 1
1. Матрицы и действия над ними. Определители 2-го и 3-го порядка. Обратная матрица и ее нахождение. Решение систем уравнений с помощью обратной матрицы. . Метод Крамера. Метод Гаусса. Теорема Кронекера-Капелли. . Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов. Коллинеарные и компланарные векторы. Разложение вектора по базису i, j, k.
2. Различные формы уравнений прямой на плоскости. Расстояние от точки до прямой. Плоскость в пространстве. Угол между плоскостями. Расстояние от точки до плоскости. Прямая в пространстве. Угол между прямыми. Угол между прямой и плоскостью. Расстояние от точки до прямой.Уравнение прямой, проходящей через две точки, параллельность прямой и плоскости, вычисление углов.
3. Предел функции. Односторонние пределы функции. Непрерывная функция. Точки разрыва и их классификация.Вычисление пределов с использованием 1-го замечательного предела. Сравнение функций. Вычисление пределов с использованием 2-го замечательного предела. Вычисление производных и дифференциалов 1-го порядка. Дифференцирование функций, заданных параметрически. Общая схема исследования функции и построение ее графика.
4. Таблица интегралов. Непосредственное интегрирование. Замена переменной в неопределенном интеграле. Интегрирование по частям в неопределенном интеграле. Интегрирование рациональных дробей. Интегрирование тригонометрических выражений. Интегрирование иррациональных выражений.
4.2 Темы практических занятий. Семестр 2
1. Функции нескольких переменных. Область определения, пределы, непрерывность. Частные производные первого и второго порядков. Экстремумы функции двух переменных.
2. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли. Уравнения старших порядков, допускающие понижение порядка. Линейные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью.
3. Признаки сходимости знакопостоянных рядов. Абсолютно и неабсолютно сходящиеся ряды. Признак сходимости Лейбница. Степенные ряды. Радиус и интервал сходимости. Ряды Тейлора. Вычисление значений функций и интегралов с помощью степенных рядов. Нахождение решений дифференциальных уравнений с помощью степенных рядов.
4. Классическая вероятностная схема. Условные вероятности. Независимость случайных событий. Формула полной вероятности и формула Байеса. Повторные испытания. Формула Бернулли и формула Пуассона. Локальная и интегральная теоремы Лапласа-Муавра. Дискретные и непрерывные случайные величины. Среднее значение и дисперсия. Элементы математической статистики. Выборка и ее представление. Выборочное среднее и выборочная дисперсия. Оценка параметров распределения по выборке.
5 Содержание и оформление контрольных работ
1. Требования к оформлению контрольных работ: контрольные работы могут выполняться на электронных носителях или в тетради (12 л.), на обложке необходимо указать номер контрольной работы, свой факультет, специальность, шифр зачетной книжки, номер варианта, свою фамилию, имя, отчество.
2. Требования к выполнению контрольной работы:
- при выполнении работы необходимо приводить основные математические формулы и промежуточные математические расчёты.
- в конце работы указывается список использованных источников, ставится число и личная подпись.