Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 632
Скачиваний: 19
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
показателя представлены в виде прямоугольников, площади которых пропорциональны.
Гистограммы используют для представления числовых данных одной категории и их изменения с течением времени. Пример — изменение численности населения страны за конкретный период.
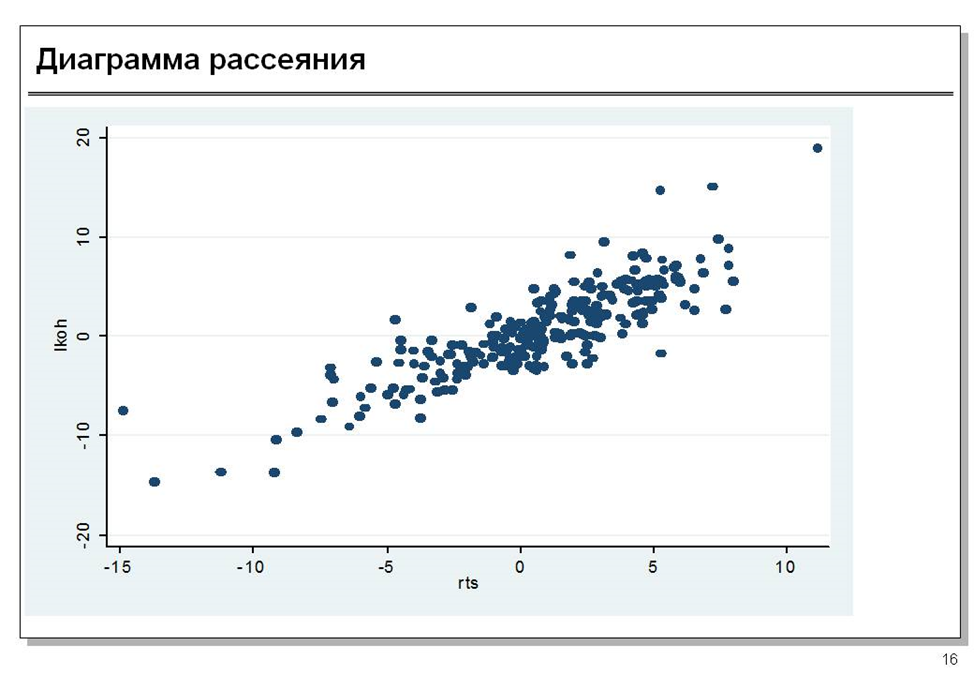
Диаграммы рассеяния (другие названия – диаграмма разброса, диаграмма рассеивания, поле корреляции)
Математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости. Могут использоваться и полярные координаты, особенно в случаях, когда одна из переменных представляет собой физическое направление или имеет циклический характер.
Диаграмма рассеяния – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.
В зависимости от наличия или отсутствия предполагаемых причинно-следственных связей при помощи диаграммы рассеяния можно анализировать зависимость:
•между влияющим фактором (причиной) и характеристикой (следствием);
•между двумя характеристиками;
•между двумя факторами.

К оглавлению
Классный тест по вопросу по ссылке
В этом материале мы с вами разберемся с тем, как отразить степень различий индивидуальных результатов в совокупности от их центральной тенденции. А если проще, то насколько в принципе субъекты могут друг от друга отличаться.
Для этого используются меры изменчивости. К ним относятся размах, дисперсия и стандартное отклонение.
Пусть перед глазами будет график, где по оси Х мы отразим все полученные нами переменные, а по оси Y – сколько людей имели тот или иной рост.
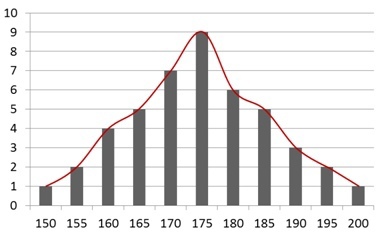
Описать его с точки
зрения центральной тенденции мы уже сможем, теперь перейдем к описанию его мер изменчивости. Начнем с простого.
Размах (range) - это разность между максимальным и минимальным значением признака.
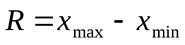
Для нашего графика размах будет равен: R = 200 (максимальный рост из нашей выборки) -150 (минимальный рост) = 50 см.
Таким образом мы отразим максимальную разницу в значениях среди нашей выборки. На основании размаха мы можем судить о близости имеющихся значений или наличии выбросов.
Вроде бы прекрасный в своей простоте метод, но его основная проблема в том, что он учитывает изменчивость нашего признака, опираясь лишь на два крайних значения. То есть ни о каком отражении совокупности речь, разумеется, не идет. А следовательно — размах крайне чувствителен к выбросам.
сли в нашу группу мы добавим одного человека с ростом в 250 см, размах увеличится в два раза (250-150=100 см), но говорить, что при этом изменилась вариативность признака, будет не совсем правильно.
В целом, получившееся у нас распределение можно назвать нормальным (об этом дальше). Но давайте предположим, что крайние значения (200 см и 150 см) это выбросы, сильно влияющие на размах. Наличие выраженных выбросов лишает смысла определение размаха, но мы все же можем это несколько нивелировать — в противном случае любое сильное отклонение сведет наши расчеты.
Чтобы избежать искажений, мы можем отсечь 25 % самых высоких и 25 % самых низких людей (то есть 1 и 4 квартили) и найти размах для оставшегося диапазона.
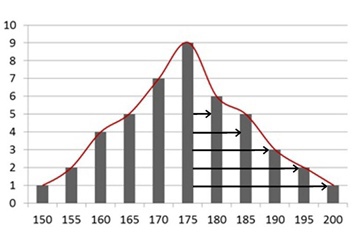
Эта мера называется межквартильным размахом, в нее входят оставшиеся 2 квартиля — то есть 50% процентов значений, наиболее близких к медиане.
Размах разумно использовать, когда изучаемое явление предсказуемо и достаточно однородно. Такая методика применима, например, при прогнозировании своих трат на покупку квартиры, или поиске работы с оглядкой на размах зарплат в регионе. Ну, а некоторые бесспорные недостатки размаха можно нивелировать
, применив межквартильный размах.
Далее пойдут понятия, которые уже невозможно объяснить на пальцах и без использования математики. Крепитесь.
Дисперсия (variance) - это средний квадрат отклонений индивидуальных значений признака в выборке от среднего арифметического этой выборки.
Дисперсия показывает, насколько в среднем все значения выборки отклоняются от среднего значения по выборке.
ремя обратиться к формуле дисперсии.
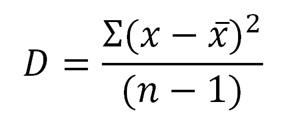
Что мы тут видим (кроме душераздирающего количества математических символов)?
Мы видим, что в числителе стоит сумма отклонений каждого из наблюдений (х-x̅) еще и возведенная в квадрат, а в знаменателе — количество этих самых наблюдений.
Дисперсия характеризует то, насколько индивидуальные значения отклоняются от среднего. Но в силу того, что она всегда представляет собой квадрат нужных нам единиц, оперировать ей не так удобно как стандартным отклонением.
Тогда что делать дальше? Вспомним, что для того чтобы избавиться от отрицательных значений, мы возвели все отклонения в квадрат.
Значит сейчас надо просто найти корень из того, что получилось. Таким образом мы получим стандартное отклонение (оно же среднеквадратичное). Если бы мы работали с генеральной совокупностью, оно называлось бы сигмой (σ).
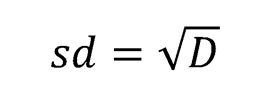
Стандартное отклонение (standart deviation) - это число, на которое отличаются все индивидуальные значения от среднего арифметического в выборке.
Гистограммы используют для представления числовых данных одной категории и их изменения с течением времени. Пример — изменение численности населения страны за конкретный период.

Диаграммы рассеяния (другие названия – диаграмма разброса, диаграмма рассеивания, поле корреляции)
Математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости. Могут использоваться и полярные координаты, особенно в случаях, когда одна из переменных представляет собой физическое направление или имеет циклический характер.
Диаграмма рассеяния – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.
В зависимости от наличия или отсутствия предполагаемых причинно-следственных связей при помощи диаграммы рассеяния можно анализировать зависимость:
•между влияющим фактором (причиной) и характеристикой (следствием);
•между двумя характеристиками;
•между двумя факторами.


5. Меры вариативности. Перечислить основные типы, написать формулу для нахождения. Какие меры вариативности подвержены выбросам в данных? Подтвердите выводы на примере.
К оглавлению
Классный тест по вопросу по ссылке
В этом материале мы с вами разберемся с тем, как отразить степень различий индивидуальных результатов в совокупности от их центральной тенденции. А если проще, то насколько в принципе субъекты могут друг от друга отличаться.
Для этого используются меры изменчивости. К ним относятся размах, дисперсия и стандартное отклонение.
Пусть перед глазами будет график, где по оси Х мы отразим все полученные нами переменные, а по оси Y – сколько людей имели тот или иной рост.

Описать его с точки
зрения центральной тенденции мы уже сможем, теперь перейдем к описанию его мер изменчивости. Начнем с простого.
Размах
Размах (range) - это разность между максимальным и минимальным значением признака.
Для нашего графика размах будет равен: R = 200 (максимальный рост из нашей выборки) -150 (минимальный рост) = 50 см.
Таким образом мы отразим максимальную разницу в значениях среди нашей выборки. На основании размаха мы можем судить о близости имеющихся значений или наличии выбросов.
Вроде бы прекрасный в своей простоте метод, но его основная проблема в том, что он учитывает изменчивость нашего признака, опираясь лишь на два крайних значения. То есть ни о каком отражении совокупности речь, разумеется, не идет. А следовательно — размах крайне чувствителен к выбросам.
сли в нашу группу мы добавим одного человека с ростом в 250 см, размах увеличится в два раза (250-150=100 см), но говорить, что при этом изменилась вариативность признака, будет не совсем правильно.
В целом, получившееся у нас распределение можно назвать нормальным (об этом дальше). Но давайте предположим, что крайние значения (200 см и 150 см) это выбросы, сильно влияющие на размах. Наличие выраженных выбросов лишает смысла определение размаха, но мы все же можем это несколько нивелировать — в противном случае любое сильное отклонение сведет наши расчеты.
Чтобы избежать искажений, мы можем отсечь 25 % самых высоких и 25 % самых низких людей (то есть 1 и 4 квартили) и найти размах для оставшегося диапазона.

Эта мера называется межквартильным размахом, в нее входят оставшиеся 2 квартиля — то есть 50% процентов значений, наиболее близких к медиане.
Размах разумно использовать, когда изучаемое явление предсказуемо и достаточно однородно. Такая методика применима, например, при прогнозировании своих трат на покупку квартиры, или поиске работы с оглядкой на размах зарплат в регионе. Ну, а некоторые бесспорные недостатки размаха можно нивелировать
, применив межквартильный размах.
Далее пойдут понятия, которые уже невозможно объяснить на пальцах и без использования математики. Крепитесь.
Дисперсия
Дисперсия (variance) - это средний квадрат отклонений индивидуальных значений признака в выборке от среднего арифметического этой выборки.
Дисперсия показывает, насколько в среднем все значения выборки отклоняются от среднего значения по выборке.
ремя обратиться к формуле дисперсии.
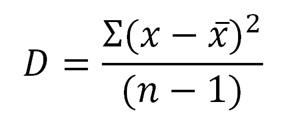
Что мы тут видим (кроме душераздирающего количества математических символов)?
Мы видим, что в числителе стоит сумма отклонений каждого из наблюдений (х-x̅) еще и возведенная в квадрат, а в знаменателе — количество этих самых наблюдений.
Дисперсия характеризует то, насколько индивидуальные значения отклоняются от среднего. Но в силу того, что она всегда представляет собой квадрат нужных нам единиц, оперировать ей не так удобно как стандартным отклонением.
Тогда что делать дальше? Вспомним, что для того чтобы избавиться от отрицательных значений, мы возвели все отклонения в квадрат.
Значит сейчас надо просто найти корень из того, что получилось. Таким образом мы получим стандартное отклонение (оно же среднеквадратичное). Если бы мы работали с генеральной совокупностью, оно называлось бы сигмой (σ).
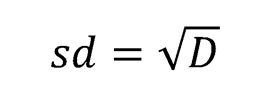
Стандартное отклонение
Стандартное отклонение (standart deviation) - это число, на которое отличаются все индивидуальные значения от среднего арифметического в выборке.
Глоссарий:
-
Размах (Range) - это разность между максимальным и минимальным значением признака -
Межквартильный размах - это разность между показателями, соответствующими первому и третьему квартилю, то есть 50% процентов значений, наиболее близких к медиане -
Дисперсия (variance) - это средний квадрат отклонений индивидуальных значений признака в выборке от среднего арифметического этой выборки. -
Стандартное отклонение (standart deviation) - это квадратный корень из дисперсии. На данное число в среднем отличаются все индивидуальные значения от среднего арифметического в выборке.