Файл: Исследование устойчивости методами Ляпунова Исследование устойчивости методом В. М. Попова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 113
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
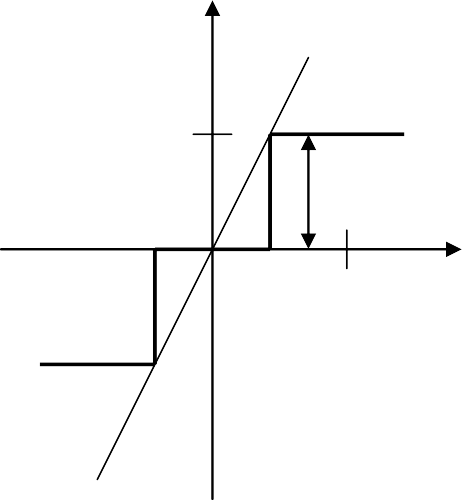
Пример 4.6. Определим методом В.М. Попова абсолютную устойчивость равновесия нелинейной САУ, состоящей из трехпозиционного релейного эле- мента (рис. 4.3.3, а) с параметрами b=1, c=8 и линейной части с АФХ

kЛe
j
1 jT
kЛ(cos jsin), 1 jT
(4.3.12)
где kЛ = 0,25; τ = 0,1 с; Т = 10 с.
Представим АФХ (4.3.12) в комплексной алгебраической форме
W( j) kЛ(cosTsin) jkЛ(sinTcos).
(4.3.13)
12T2 12T2
Соответственно (4.3.11) модифицированная АФХ (рис. 4.3.3, б) запишется
W*( j) 0,25(cos0,110sin0,1) j0,25(sin0,110cos0,1).(4.3.14)
11002 11002
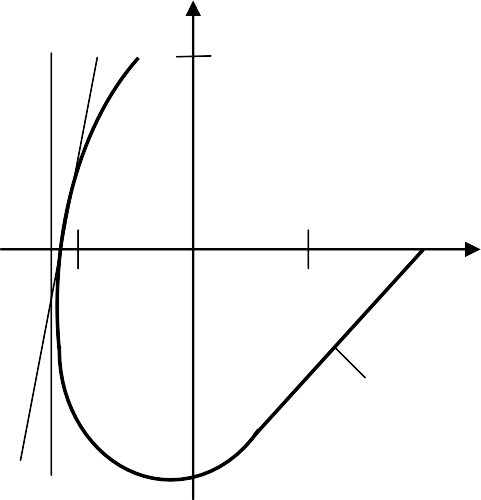
Нелинейная характеристика (рис. 4.3.3, а) располагается внутри сектора, ограниченного прямой с наклоном k=c/b=8/1=8, проходящей через начало ко- ординат под углом α=arctgk=arctg8=82,8º. Модифицированная АФХ, постро- енная по формуле (4.3.14), имеет вид, представленный на рис. 4.3.3, б. Для са- мого неблагоприятного случая из (4.3.10) при q→0 (arctg 1/q→90º) проводим вертикальную прямую 1 через точку с координатами (–1/k= –1/8= –0,125; j0), которая не пересекается с W*(jω) (АФХ располагается справа от этой прямой). Следовательно, равновесие нелинейной САУ при данных параметрах абсолют- но устойчиво.
 у k=c/b
у k=c/b8
c
jωQ()
 1 2
1 20,1
0 b2 x–0,1 0,1 P()
W*(j)
а б
Рис. 4.3.3. Определение абсолютной устойчивости Рассмотренный метод также позволяет решать обратные задачи определе-
ния допустимых по условиям абсолютной устойчивости изменений параметров нелинейности. Например, для определения допустимого уменьшения зоны не- чувствительности bД, приводящего к повышению крутизны k, проведем каса- тельную 2 к характеристике W*(j), которая отражает границу устойчивости САУ при уменьшении значения модуля 1/k. Касательная 2 пересекает действи- тельную ось комплексной плоскости в точке 1/kД – 0,117. Следовательно гра- ница увеличения углового коэффициента kД = 1/0,117 8,55; а для минимальной
зоны нечувствительности bД = c/kД =8/8,55 0,936. Приb 0,936 состояние равновесия системы будетнеустойчивым.
- 1 2 3 4 5 6 7
Алгебраический метод анализа автоколебаний
Для исследования возможности возникновения устойчивых авто- колебаний в нелинейной САУ и определения их амплитуды можно воспользоваться критерием Гурвица [13, 15]. Для этого безынерцион- ный нелинейный элемент заменяется усилительным звеном с гармо- нически линеаризованным коэффициентом передачи J(A), зависящим от амплитуды А входного сигнала, и на основе методов теории ли- нейных САУ составляется характеристическое уравнение линеаризо- ванной замкнутой САУ. Из коэффициентов этого уравнения состав- ляются определители Гурвица, которые будут функциями амплитуды автоколебаний. Приравнивая определители Гурвица нулю и решая полученные алгебраические уравнения, находится граница устойчи- вости САУ. Из уравнения границы устойчивости определяется ам- плитуда возможных автоколебаний.
Для проверки устойчивости автоколебаний следует дать прира- щение рассчитанной амплитуде возможных автоколебаний. Если при увеличении амплитуды определители Гурвица становятся положи- тельными, а при уменьшении – отрицательными, то в нелинейной САУ имеют место устойчивые автоколебания. Это объясняется тем, что при увеличении амплитуды колебаний условия устойчивости САУ выполняются и амплитуда колебаний уменьшается, пока не ста- нет равной амплитуде автоколебаний. При уменьшении амплитуды колебаний САУ становится неустойчивой и амплитуда колебаний возрастает до амплитуды автоколебаний.
Если увеличение амплитуды колебаний приводит к невыполне- нию условий устойчивости, то в САУ будут расходящиеся колебания.
Если уменьшение амплитуды колебаний приводит к выполнению условий устойчивости, то в САУ будут затухающие колебания.
Пример 4.7. Определим возможность возникновения автоколебаний и их амплитуду в нелинейной САУ, содержащей НЭ с зоной нечувствительности а=±4 В и единичным коэффициентом наклона линейной части (tgα=1), если ха- рактеристическое уравнение линеаризованной замкнутой САУ, где НЭ пред- ставлен безынерционным звеном с гармоническим коэффициентом передачи J(A), имеет вид
M( p, A) 0,05 p3 1,05 p2 [110J( A)] p100 0.
(4.3.15)
Гармонический коэффициент передачи J(A) нелинейного элемента (НЭ) представляет собой отношение первой гармонической составляющей на выходе
НЭ y1 C1exp j(t1)
к гармоническому сигналу на входе НЭ
x Aexp jt,
выраженных в комплексной форме
C1e j(t1)
C1cos1 jC1sin1
или
J( A)
Aejt A ,
(4.3.16)
(4.3.17)
где C1
B2 D2
-
амплитуда первой гармонической составляющей на выходе

1 1
НЭ y1 B1sint D1cost;
1 ar c t gD(1 B/1
-
сдвиг фазы первой гармоники
нелинейным элементом; q(A) и q′(A) – коэффициенты гармонической линеа- ризации НЭ.
Для безынерционных НЭ гармонический коэффициент передачи зависит только от амплитуды q(A), поскольку q′(A)=0.
Для определения гармонического коэффициента передачи НЭ с зоной не- чувствительности найдем амплитуду первой гармоники выходного сигнала
C 1 2 y()sin d 4 /2 y()sin d,
(4.3.18)
1
0 0
где ψ=ωt.
Из-за наличия у НЭ зоны нечувствительности ± а синусоидальный сигнал на выходе НЭ будет отсутствовать y(ψ)=0 в пределах 0<ψ<β, где β=arcsin(a/A), а в пределах β ≤ ψ ≤ π/2 его амплитуда будет срезана y(ψ)=tgα(Asinψ – a), где α – угол наклона линейной части характеристики. В результате из (4.3.18) по- лучим
C 4tg/2 Asin2 d a/2sin d

2 sin2
A1 tg.
(4.3.19)
1
0
Тогда гармонический коэффициент передачи НЭ с зоной нечувствительно- сти определится формулой
J( A) C1 1 2sin2tg.
(4.3.20)
A
На практике для удобства исследований может использоваться нормиро- ванный гармонический коэффициент передачи, который является не функцией амплитуды А, а функцией относительной амплитуды A/a, т. е. отношения ам- плитуды к параметру нелинейности при постоянном наклоне линейной части нелинейной характеристики tgα=1
где β=arcsin(a/A).
J(A/a) 1(2sin2)/ J( A)/tg,
(4.3.21)
Из характеристического уравнения линеаризованной замкнутой САУ (4.3.15) на основании критерия Гурвица для системы третьего порядка находим уравнение для границы устойчивости