Файл: Исследование устойчивости методами Ляпунова Исследование устойчивости методом В. М. Попова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 107
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лекция 10 Тема. НЕЛИНЕЙНЫЕ САУ
-
Устойчивость нелинейных САУ -
Понятие устойчивости нелинейных САУ -
Исследование устойчивости методами Ляпунова -
Исследование устойчивости методом В.М. Попова -
Алгебраический метод анализа автоколебаний
-
Особенности нелинейных САУ
САУ называется нелинейный, если имеет хотя один нелинейный элемент (НЭ), который описывается нелинейным уравнением (обла- дает нелинейной характеристикой) [1, 9, 13, 15]. Строго говоря, все реальные САУ являются нелинейными из-за естественных ограниче- ний возрастания выходного значения напряжения, мощности, скоро- сти и других физических величин, а также нелинейностей их взаимо- зависимостей (насыщение, люфт, зона нечувствительности и др.).
По виду нелинейного уравнения «вход-выход» НЭ делятся на бе- зынерционные (статические) и инерционные (динамические).
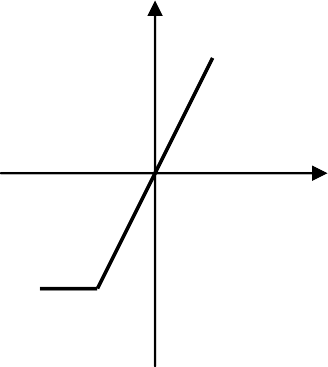
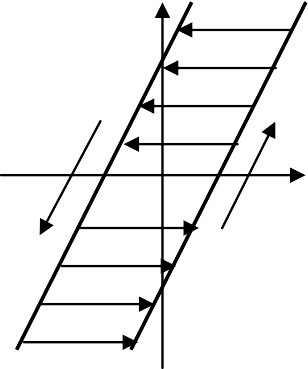
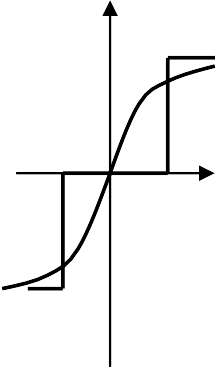
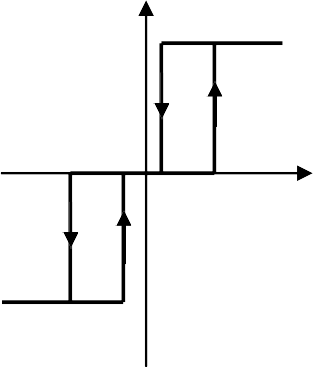
Безынерционные (статические) НЭ мгновенно реагируют на входное воздействие xсоответственно статической нелинейной ха- рактеристике выходной величины y=F(x), которая может быть непре- рывной или релейной (рис. 4.1.1, а), типа ограничение (рис. 4.1.1, в), типа люфт (рис. 4.1.1, г), однозначной или неоднозначной. В послед- нем случае (гистерезисные петли) величина yзависит от входной ве- личины xи от направления ее изменения (рис. 4.1.1, б).
 у у у y
у у у y0 х 0 х 0 х 0x
а б в г
Рис. 4.1.1. Характеристики нелинейных элементов
Инерционные (динамические) НЭ описываются дифференциаль- ным уравнением зависимости выходной величины yот входной вели- чины xи ее производных, например, y=F(x, dx/dt).
В САУ также используются особые нелинейности (множительное звено, элементы с переключаемой структурой или параметрами, эле- менты логического типа и т.п.), улучшающие качество САУ и обес- печивающие оптимальное и адаптивное управление процессами.
Присутствие нелинейностей обычно ухудшает качество работы линейных САУ – увеличиваются ошибки управления, ухудшается ус- тойчивость и т.д. Однако, в некоторых случаях нелинейности вводят
в САУ специально – для ограничения тока или скорости двигателя на заданном уровне, для достижения максимального быстродействия САУ за счет применения релейного регулятора, для улучшения свойств САУ за счет введения нелинейных корректирующих уст- ройств и т. д. [1, 9, 13, 15].
Нелинейные САУ отличаются от линейных САУ тем, что к ним неприменим принцип суперпозиции (наложения), а переходные про- цессы и динамическая устойчивость зависят от величины и формы внешних воздействий. Поэтому для нелинейных САУ существуют понятия «устойчивость в малом», «устойчивость в большом», «ус- тойчивость в целом» соответствующих устойчивости САУ только при малых, больших или любых начальных внешних воздействиях. Особенностями нелинейных САУ также является возможность воз- никновения в них установившихся рабочих режимов автоколебаний, т.е. устойчивых собственных колебаний с постоянной амплитудой, не превышающей допустимого значения при отсутствии внешних коле- бательных воздействий [1, 9, 13, 15].
Для упрощения расчетов структуру нелинейных САУ путем эк- вивалентных структурных преобразований стараются представить в виде одноконтурной, с последовательно соединенными нелинейным звеном F(x) и линейной динамической частью W(p) [1, 13, 15]. Струк- турные преобразования нелинейных САУ проводят при неизменно- сти входных воздействий нелинейных элементов.
При исследованиях нелинейных САУ обычно решают задачи оценки влияния нелинейностей на процессы в САУ с линейной ча- стью или задачи анализа и синтеза нелинейных САУ, которые специ- ально проектируются как нелинейные.
Контрольные вопросы
-
Почему возникают нелинейности в САУ? -
Какие нелинейности относятся к статическим, динамическим и особым? -
Для чего нелинейности могут специально вводиться в САУ? -
Какие основные отличия и особенности имеют нелинейные САУ по от- ношению к линейным САУ? -
Какие две основные задачи обычно решаются при исследованиях нели- нейных САУ? -
Какие условия следует выполнять при эквивалентных преобразованиях структурных схем САУ, содержащих нелинейный элемент?
- 1 2 3 4 5 6 7
Методы исследования нелинейных САУ
Поскольку общие аналитические методы решения нелинейных дифференциальных уравнений отсутствуют, то при анализе и синтезе нелинейных САУ используются приближенные методы решения практических задач. Эти методы можно разделить на две группы [15]:
1) методы, основанные на приближенном решении нелинейных диф- ференциальных уравнений (методы «припасовывания», фазовых тра- екторий, точечных преобразований, графо-аналитические, частотный В.М. Попова, численные, моделирования); 2) методы, использующие линеаризацию нелинейных характеристик звеньев САУ с последую- щим применением хорошо разработанных методов анализа и синтеза линейных САУ (методы малого параметра, гармонического баланса, статистической линеаризации). Рассмотрим часто используемые для расчетов переходных процессов в нелинейных САУ методы припасо- вывания, фазовых траекторий, гармонической линеаризации.
Метод припасовывания [1, 13, 15] заключается в том, что нели- нейная характеристика заменяется несколькими линейными участка- ми и на каждом участке решается система линейных дифференциаль- ных уравнений САУ. Полученные решения припасовывают (сшива- ют), принимая конечные значения решения и его производных на предыдущем участке за начальные условия решения на последующем участке. Метод характеризуется громоздкостью расчетов.

K3 =1




b=2
x
–b=–2
K1 0,01
=
p p
K2
1
x F(x) x2 x1

=
p
p


K4 = 5
Рис. 4.2.1. Нелинейная САУ
Из схемы получается следующая система дифференциальных уравнений

x K4 x1 K3x2.
(4.2.1)
В зависимости от знака координаты xсистема уравнений (4.2.1), описы- вающая движения САУ, распадается на две линейные системы уравнений:
при x<0
при x>0
x1 K2x2;

Kb;
x2 1

x2 1
Kb.
(4.2.2)
(4.2.3)
Проинтегрировав вторые уравнения в (4.2.2) и (4.2.3), получим
x2 K1btc1 при x<0; (4.2.4)
x2 K1btc2 при x>0. (4.2.5)
Постоянные интегрирования определяются из начальных условий. Под- ставляя значения x2 из (4.2.4) и (4.2.5) в первые уравнения систем (4.2.2) и (4.2.3) и интегрируя полученные уравнения, получаем выражения
x1 K1K2bt2 /2 K2c1tc3
x1 K1K2t2 /2 K2c2tc4
при x<0; (4.2.6)
при x>0. (4.2.7)