Файл: Исследование устойчивости методами Ляпунова Исследование устойчивости методом В. М. Попова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 110
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ния возмущенного движения в ряд Тейлора, что требует дополнительных ис- следований.
Данные теоремы Ляпунова позволяют исследовать устойчивость нелинейной САУ методами теории линейных систем. Однако эти ме- тоды применимы только к системам с гладкими нелинейностями.
Второй (прямой) метод Ляпунова более универсален и не тре- бует решения дифференциальных уравнений [1, 13, 15]. Метод позво- ляет выявить достаточные условия устойчивости на основе качест- венной теории уравнений и совместного использования уравнений движения системы в фазовом пространстве и специальной функции Ляпунова V(x).
Функции Ляпунова V(x) являются аналогами потенциальных функций в потенциальном поле фазовых координат системы
выражающих потенциальную энергию, достигающую
минимума в начале координат. Функция V(x) называется знакоопре- деленной, если в рассматриваемой области, содержащей начало коор- динат, сохраняет один и тот же знак и обращается в нуль только в на-
чале координат (например, при n=3 это
V a2 x2 b2 x2 c2 x2 ).
Знако-

1 2 3
определенная функция V(x) может быть положительно определенной или отрицательно определенной. Если функция V(x) сохраняет один и тот же знак, но обращается в нуль не только в начале координат, то такая функция называется знакопостоянной (положительной или от-

3
рицательной). Например, при n=3 V(x1 x2 )2 cx2 обращается в
нуль при x2 x1 и при x3 0 . Наконец, функция V(x) называется зна-
копеременной, если она в рассматриваемой области не сохраняет
один и тот же знак (например, функция V x1 x2 x3 ).
При исследовании устойчивости нелинейных САУ прямым мето- дом Ляпунова изучается поведение функции V(x) вдоль фазовых тра- екторий, определяемых уравнениями движения. Если функция V(x) имеет отрицательную производную во времени (dV/dt)<0, то с воз- растанием времени она убывает и фазовая траектория пересекает по- верхности убывающего уровня функции V(x) по направлению к нача- лу координат. Это соответствует устойчивой системе.
Для этих случаев А.М. Ляпуновы сформулировал следующие теоремы [1, 15].
Теорема 1. Если существует знакоопределенная функция V(x1, x2, ..., xn), полная производная которой по времени dV/dt в силу дифференциальных урав- нений является знакопостоянной функцией противоположного с V(x) знака, то невозмущенное движение устойчиво.
Теорема 2. Если существует знакоопределенная функция V(x1, x2, ..., xn), полная производная которой по времени в силу дифференциальных уравнений является знакоопределенной функцией противоположного с V(x) знака, то не- возмущенное движение асимптотически устойчиво.
Теорема 3. Если существует знакопостоянная функция V(x1, x2, ..., xn), пол- ная производная которой по времени в силу дифференциальных уравнений явля- ется знакопостоянной функцией одинакового с V(x) знака, то невозмущенное движение неустойчиво.
Теорема 4. Если существует знакоопределенная функция V(x1, x2, ..., xn, t), полная производная по времени которой в силу дифференциальных уравнений является знакопостоянной, или тождественно равной нулю функцией, то не- возмущенное движение устойчиво.
Теорема 5. Если существует функция V(x1, x2, ..., xn, t), удовлетворяющая условиям предыдущей теоремы, допускающая бесконечно малый высший пре- дел, а производная которой представляет знакоопределенную функцию проти- воположного с V знака, то невозмущенное движение асимптотически устой- чиво.
Приведенные теоремы дают только достаточные, но не необходимые усло- вия устойчивости или неустойчивости САУ и не указывают пути нахождения подходящих функций V, в чем состоит основная трудность применения данного метода.
y ky k1( y)3 y 0
[15].
Обозначим
x1 y;
x1 x2
и получим уравнения в форме Коши
(4.3.8)
3

1 2
Выберем функцию Ляпунова в виде V(x1,x2) x2 x2,
поскольку ее произ-
водная по времени после подстановок выражений
x1 и
x2 из дифференциаль-
ных уравнений (4.3.8) САУ
dV/dt2(kx2 kx4)
отрицательна и равна нулю

2 1 2
только в начале координат. Кривые V=const являются окружностями с центром в начале координат, а отрицательный знак производной dV/dtуказывает на при- ближение фазовой траектории к началу координат с течением времени, что по теореме 2 соответствует асимптотически устойчивой нелинейной системе.
- 1 2 3 4 5 6 7
Исследование устойчивости методом В.М. Попова
Обширный класс нелинейных САУ имеет структуру из линейной части и нелинейного элемента (рис. 4.2.4) с различными нелинейны- ми статическими характеристиками класса y=F(x), расположенными в заданном угле arctg k(рис. 4.3.2, а). Разнообразие и нестабильность нелинейных характеристик в таких САУ приводят к необходимости
их абсолютной устойчивости, при которой достигается асимптотиче- ская устойчивость в целом при любой нелинейности внутри заданно- го класса нелинейностей. Однако сложность решения этой задачи дол- гое время ограничивала возможности ее практической реализации.
В 1960 г. румынский ученый В.М. Попов предложил использо- вать метод частотных характеристик для решения задачи абсолютной устойчивости нелинейных САУ с однозначной статической нелиней- ностью F(x) любого вида, расположенной в угловом секторе между осью абсцисс и прямой с угловым коэффициентом k(рис. 4.3.2, а) [1, 13, 15].
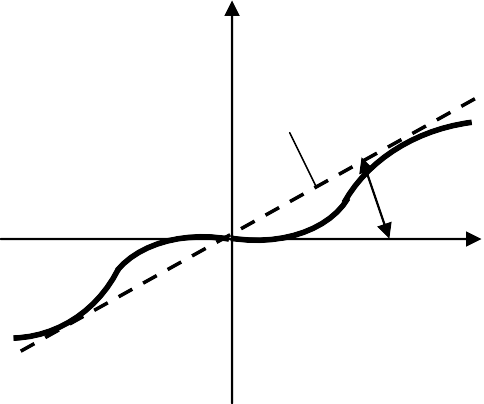 y
yk
arctg k
arctg1/q JωQ(ω)
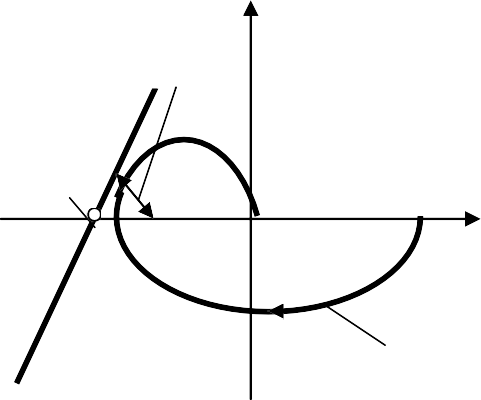 –1/k
–1/k0 х 0 P()
W*(j)
а б
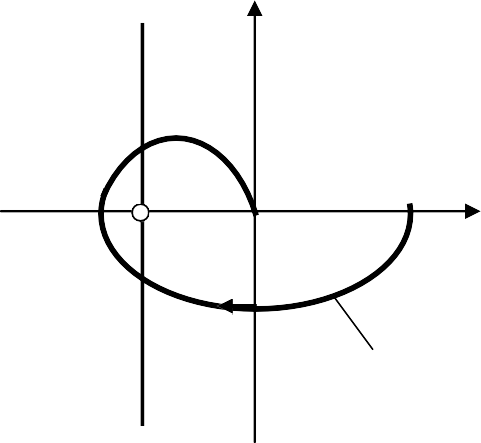
 jωQ() jωQ()
jωQ() jωQ()–1/k –1/k
0 P() 0 Р()
W*(j) W*(j)
в г
Рис. 4.3.2. Критерий абсолютной устойчивости В.М. Попова
Пусть в нелинейной САУ линейная часть имеет W(p)=P(p)/Q(p), где характеристическое уравнение Q(p)=a0pn+a1pn–1+ ...+an–1p+an=0 имеет все левые корни и не более двух нулевых корней a0=0 и a1=0, а однозначная нелинейность не выходит за пределы заданного угла arctg k
0<y=F(x)<kx; F(x=0)=0. (4.3.9)
Для таких САУ В.М. Попов сформулировал следующую теорему: для установления устойчивости нелинейной системы достаточно подобрать такое конечное действительное число
q, при котором при всех ω≥0 вещественная часть функции
Re[(1+jωq)W(jω)+1/k]>0, (4.3.10)
где W(jω) – АФХ линейной части САУ, получаемой из W(p) при р=jω.На границе устойчивости, при X=Re[W(jω)]; Y=ωIm[W(jω)], из (4.3.10) получим уравнение прямой Попова X–qY+1/k=0, проходящей
через точку (–1/k; j0) c наклоном 1/q.
При наличии одного нулевого корня также требуется, чтобы ImW(jω)→ – ∞ при ω→∞, а при двух нулевых корнях требуется, что- бы ReW(jω)→ – ∞ при ω→0, а ImW(jω)<0 при малых значениях ω.
Удобная графическая интерпретация теоремы В.М. Попова полу- чается при введении модифицированной АФХ линейной части САУ [1, 15]
W*( j) P*() jQ*() P() jT0Q(),
где Т0=1 сек – нормирующий множитель [1].
(4.3.11)
В этом случае из теоремы В.М. Попова получается следующая
формулировка критерия устойчивости: для абсолютной устойчиво- сти нелинейной системы с одним безынерционным нелинейным эле- ментом, нелинейная характеристика которого лежит в секторе (0, k) (рис. 4.3.2, а), достаточно, чтобы на плоскости модифициро- ванной частотной характеристики W*(j) через точку (–1/k, 0) можно было провести прямую Попова так, чтобы характеристика W*(j) лежала справа от этой прямой[15].
На рис. 4.3.2, б показан случай, когда критерий удовлетворяется, а на рис. 4.3.2, в, г – случаи, когда критерий не удовлетворяется.
Графические формулировки критерия устойчивости В.М. Попова требуют чтобы АФХ линейной части САУ не охватывала точку (–1/k, j0) на комплексной плоскости, аналогично частотному критерию Найквиста-Михайлова для линейных САУ, по которому АФХ не должна охватывать точку (–1, j0).
Достоинства метода В.М. Попова состоят в простоте графической формы его применения при любой сложности линейной части САУ и численно заданных коэффициентах; при возможности использования только экспериментально снятой характеристики W(jω) линейной части САУ, которую нужно перестроить в W*(jω); при неизвестной нелинейности и известных лишь пределах угла, в котором она распо- лагается.