Файл: Исследование устойчивости методами Ляпунова Исследование устойчивости методом В. М. Попова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 104
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
aaa
при a<bхарактеристика линейна и q(a)=k; для двухпозиционного реле с сим- метричной характеристикой и петлей гистерезиса шириной ± bпри a>bи выходном сигнале ± S
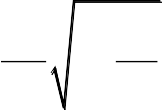4S b24Sb
KH (q,q') q(a) a1 p, a2 a2
q' 0;
(4.2.56)
для характеристики люфт с зазором ± b и наклоном k(рис. 4.1.1, г)
q(a) k arcsin1 2b 21 2b b1 b,
2
a
a a
a
q'(a) 4kb1 b
при
a b;
(4.2.57)
a a
KH (q,q') q(a) q'(a) p.
Контрольные вопросы
-
Как делятся методы исследования нелинейных САУ на две группы? -
На каком принципе основан метод припасовывания? -
На каком принципе основан метод фазовых траекторий? -
Что называется фазовым портретом нелинейной системы? -
Что называется изоклинами и как по ним строят фазовую траекторию? -
На каком принципе основан метод гармонической линеаризации? -
Какая операция называется гармонической линеаризацией НЭ? -
Как получить операторную передаточную функцию (ОФП) НЭ? -
Как получить амплитудно-фазовую характеристику НЭ?
Устойчивость нелинейных САУ
-
Понятие устойчивости нелинейных САУ
Понятие устойчивости в нелинейных САУ оказывается более сложным, чем в линейных САУ. Впервые понятие и основные теоре- мы устойчивости нелинейных систем в 1892 г. сформулировал осно- воположник теории устойчивости русский ученый А.М. Ляпунов [1, 9, 13, 15].
Для определения устойчивости нелинейной САУ предположим, что ее состояние описывается системой дифференциальных уравнений
dyi/dt Fi( y1, y2, , yn),i1, 2, , n.
(4.3.1)
Из совокупности возможных решений уравнений (4.3.1) при раз-
i
ных начальных условиях выберем одно решение y(t) с начальными
условиями y(t) , которое по терминологии А.М. Ляпунова примем
i0
за невозмущенное движение, а всякое другое движение
yi(t)
с други-
ми начальными условиями
жением.
yi(t0 )
будем называть возмущенным дви-
Обычно за невозмущенное движение выбирается расчетное дви- жение системы в рабочем режиме, а возмущенное движения появля- ется при изменении начальных условий или внешних воздействий.
Устойчивость удобнее рассматривать, используя уравнения в от-
i
клонениях процесса yi(t) от невозмущенного движения y(t) [13]
i
xi(t) yi(t) y(t),
i1, 2, , n.
(4.3.2)
Тогда система уравнений возмущенного движения в отклонениях
dxi /dtФi(x1,x2, ,xn),i1, 2, , n,
(4.3.3)
а невозмущенное движение в отклонениях будет иметь все
x*(t) 0.
i
В фазовом пространстве в координатах отклонений xi(t) с добав- ленной осью времени tотклонение невозмущенного движения
x*(t) 0
представляется прямой линией, совпадающей с осью време-
ни t, а отклонение возмущенного движения xi(t) имеет определенную фазовую траекторию (рис. 4.3.1).
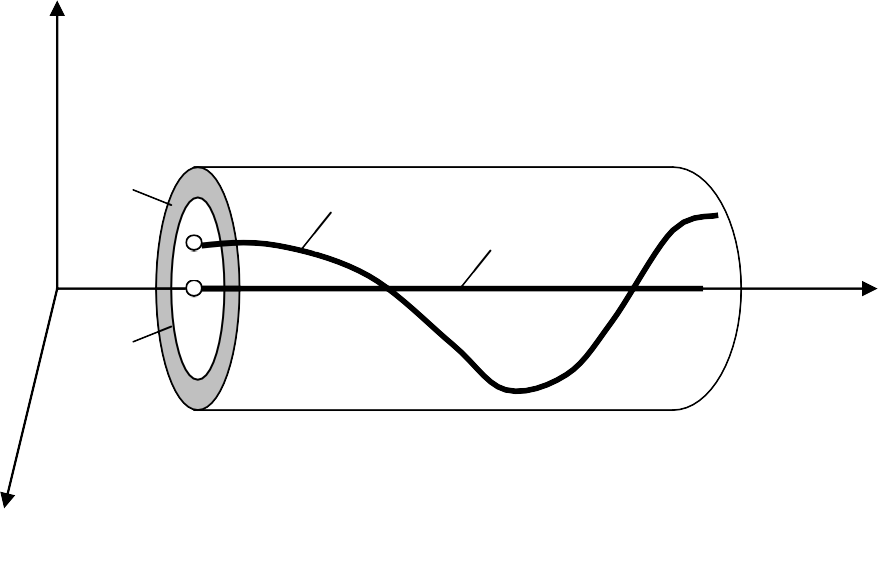x2 , x3 , . . . , xnε x(t)
δ
x=0
t
x1
Рис. 4.3.1. Фазовые траектории системы в отклонениях
Невозмущенное движение называется устойчивым по Ляпунову, если, задав в фазовом пространстве координат системы трубку сколь угодно малого n-мерного сечения ε>0, можно подобрать такую об- ласть начальных условий δ(ε)>0 для всех возмущенных движений xi(t), что при изменении t0 ≤ t ≤∞ они не выйдут из заданной трубки ε.
Аналитически понятие устойчивости формулируется так: невоз-
мущенное движение называется устойчивым по Ляпунову, если для всякого сколь угодно малого ε>0 можно указать такое δ(ε)>0, что при
xi(t0 (i1,2, ,n)
(4.3.4)
при движении системы при всех значениях t≤ t0 выполняется условие
xi (i1,2, ,n).
(4.3.5)
Невозмущенное движение неустойчиво, если условие (4.3.5) не
выполняется хотя бы для одной из координат
xi(t).
Если (4.3.4) и (4.3.5) выполняются и все
xi(t) 0
при t, то
невозмущенное движение называется асимптотически устойчивым.
Если
xi(t) 0
при t→∞ после любых начальных отклонений, то сис-
тема называется устойчивой в целом. САУ с абсолютной устойчиво- стью обладают асимптотической устойчивостью в целом при любом из типов нелинейностей определенного класса.
Для определения устойчивости автоколебаний вводится понятие орбитальной устойчивости САУ. При этом в фазовом пространстве автоколебания представляются замкнутой кривой, называемой пре- дельным циклом, которую обегает изображающая точка за время од- ного периода колебаний.
В нелинейных системах, в отличие от линейных, устойчивость равновесия не означает устойчивости всех процессов, поскольку свойства нелинейной системы изменяются при изменении координат состояния системы. Например, нелинейная САУ второго порядка при наличии предельного цикла имеет устойчивость в состоянии равнове- сия, но оказывается неустойчивой при больших начальных воздейст- виях, выходящих за границу предельного цикла, т. е. САУ устойчива в малом и неустойчива в большом.
- 1 2 3 4 5 6 7
Исследование устойчивости методами Ляпунова
Первый метод Ляпунова основан на линеаризации нелинейного уравнения движения системы с разложением нелинейных функций в ряд Тейлора и учетом только членов первого порядка [1, 13, 15].
Представим уравнения движения системы в видегде
aijFi/x
dxi/dt ai1x1 ai2 x2 ainxni(x1, x2 , , xn), (i, j1, 2, , n).
(4.3.6)
Линейные уравнения первого приближения из (4.3.6) будут
dxi/dt ai1x1 ai2 x2 ainxn(i1,2, ,n).
(4.3.7)
Для этих случаев А.М. Ляпунов доказал следующие теоремы [1, 13, 15]. Теорема 1. Если все корни характеристического уравнения системы пер-
вого приближения (4.3.7) имеют отрицательные вещественные части, то не- возмущенное движение нелинейной системы асимптотически устойчиво при любых членах высших порядков в уравнениях возмущенного движения (4.3.6).
Теорема 2. Невозмущенное движение неустойчиво, если среди корней ха- рактеристического уравнения первого приближения (4.3.7) хотя бы один ко- рень имеет положительную вещественную часть.
Теорема 3. Если характеристическое уравнение системы первого прибли- жения (4.3.7) имеют нулевые корни, то устойчивость нелинейной системы должна определяться с учетом членов высших порядков в разложенииуравне-