Файл: Исследование устойчивости методами Ляпунова Исследование устойчивости методом В. М. Попова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 106
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Уравнения (4.2.4) – (4.2.7) являются уравнениями искомого переходного процесса. Построение переходного процесса производится по (4.2.4) и (4.2.6) при x<0 и по (4.2.5) и (4.2.7) при x>0. Начальное движение определяется зна- ком координаты x(0) при t=0. Подставив численные значения параметров и на- чальных условий в третье уравнение системы (4.2.1), получим
x(0) K4x1(0) K3x2(0) 50,0110 0,050.
Поскольку x(0)>0, то для построения переходного процесса на первом уча- стке нужно использовать уравнения (4.2.5) и (4.2.7). Из (4.2.5) и (4.2.7) при t=0 определяем постоянные интегрирования с2=x2(0)=0, c1=x1(0)=0,01.
Уравнения движения на первом участке переходного процесса будут
x2(t) 0,02t;
x1(t) 0,01t2 0,01.
(4.2.8)
(4.2.9)
Движение по уравнениям (4.2.8) и (4.2.9) будут продолжаться до измене- ния знака координаты xв момент времени t1 при
1
x K4x1 K3x2 5(0,01t2 0,01) 10,02t1 0,
откуда t1=0,82 сек.
Значения x1 и x2 в конце первого участка будут по (4.2.8) и (4.2.9)
1
x1(t1) 0,01t2 0,010,00328;
x2(t1) 0,02t1 0,0164.
(4.2.10)
(4.2.11)
Эти значения будут начальными для второго участка переходного процес- са. Подставляя значения x1 и x2 из (4.2.10) и (4.2.11) в (4.2.6) и (4.2.4) и полагая в них t=0 (начав расчет процесса на втором участке), находим с3=0,00328 и с1=–0,0164 для второго участка. Уравнения (4.2.6) и (4.2.4) для второго участка
x1 0,01t2 0,0164t0,00328;
x2 0,02t0,0164.
(4.2.12)
2
Подставляя уравнения из (4.2.12) в третье уравнение системы (4.2.1) и приравнивая его нулю, находим момент переключения t2 в конце второго этапа x K4x1 K3x2 5(0,01t2 0,0164t2 0,00328)1(0,02t0,0164) 0;t2 1,24сек.
Подставляя t2 в уравнения (4.2.12), находим значения в конце второго этапа
x1(t2) 0,00168; x2(t2) 0,0084, которые являются начальными для третьего
этапа расчета переходного процесса. На участке t1 – t2 координата x1 изменяется по параболе и достигает экстремума в момент времени, при котором ее произ-
водная x1 0,02t0,0164 0, откуда tЭ2=0,82 сек. Находим из (4.2.12) максимумкоординаты x1(tЭ2)=0,01∙0,822–0,0164∙0,82+0,00328=–0,0034.
Далее построение переходного процесса производится в том же порядке.
Метод фазовых траекторий основан на представлении движе- ния системы в фазовом пространстве и анализе совокупности фазо- вых траекторий и особых точек без непосредственного интегрирова- ния ее нелинейных дифференциальных уравнений [1, 13, 15].
Для исследования нелинейной САУ методом фазовых траекторий все звенья САУ, допускающие линеаризацию, описываются линей- ными уравнениями, а одно (реже – два или несколько) существенно нелинейных звеньев описываются нелинейными уравнениями.
В общем случае система нелинейных дифференциальных уравне- ний САУ в нормальной форме записывается в виде
dxidtФix1, x2 , , xn,t; g(t); f(t),
i1, 2, , n;
(4.2.13)
гдеxi(i1, 2, , n)
– координаты состояния САУ; g(t), f(t) – внешние
задающее и возмущающее воздействия; t– текущее время.
Для анализа собственных свойств САУ (анализа переходных процессов, вызванных ненулевыми начальными значениями коорди- нат при отсутствии внешних воздействий), уравнения (4.2.13) для стационарных систем (с постоянными параметрами) принимают вид
dxi dtФi (x1, x2 , , xn),
i1, 2, , n.
(4.2.14)
Значения координат xiможно представить в виде координат точ- ки M(x1, x2, ..., xn) в n-мерном пространстве, которое называется фазо- вым пространством. Точку М(x1, x2,..., xn) называют изображающей точкой, а линию, по которой она перемещается при изменении со- стояния системы, называют фазовой траекторией.Каждой совокупности начальных условий хi(0) соответствует единственное решение системы дифференциальных уравнений, толь- ко одна начальная точка и единственная фазовая траектория в фазо- вом пространстве. Ряду совокупностей начальных условий соответст- вует семейство непересекающихся фазовых траекторий, которое на- зывается фазовым портретом системы.
Метод фазовых траекторий наиболее удобен для исследования систем второго порядка, так как их фазовые траектории располагают- ся на одной фазовой плоскости двух переменных. Фазовый портрет этих систем можно построить непосредственно по дифференциаль- ному уравнению, не решая его. При этом в качестве переменных, от- кладываемых по осям абсцисс и ординат фазовой плоскости, обычно выбирают регулируемую величину xи скорость ее изменения y=x′ (или ошибку системы ε и скорость ее изменения ε′). Тогда свободныедвижения в САУ второго порядка с уравнением
x F1(x)x F2 (x) 0
можно описать двумя уравнениями первого порядка
y x dx;y dyF1(x) y F2 (x),
(4.2.15)
dtdt
откуда, исключая время, получаем дифференциальное уравнение фа- зовой траектории системы
dy F1(x) F2 (x). dxy(4.2.16)
Интегрирование уравнения (4.2.16) дает уравнение фазовой тра- ектории в явном виде
y F(x) C,
где С – постоянная интегрирования из начальных условий.
(4.2.17)
Точки равновесного состояния системы определяются нулевыми
значениями скорости изменения координат dx/ dt 0, dy/ dt 0, что
создает неопределенность в правой части уравнения (4.2.16) (деление на y=0). Поэтому точки равновесного состояния системы являются так называемыми особыми точками на фазовой плоскости.
Обычно фазовые траектории на фазовой плоскости строят для свободных движений системы, однако их можно строить и для выну- жденных движений при известном задающем воздействии.
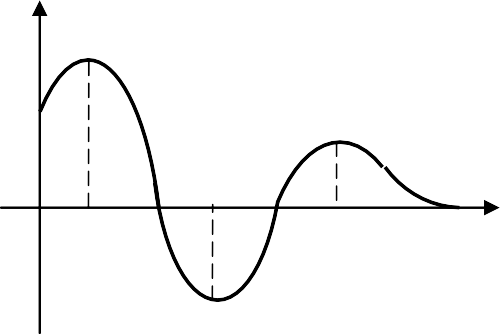
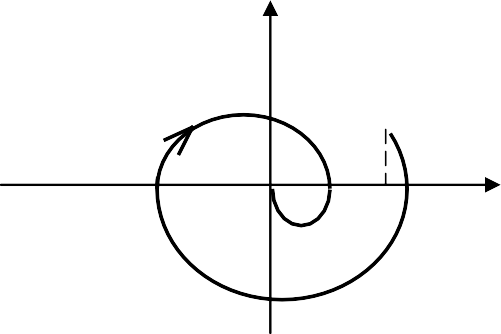
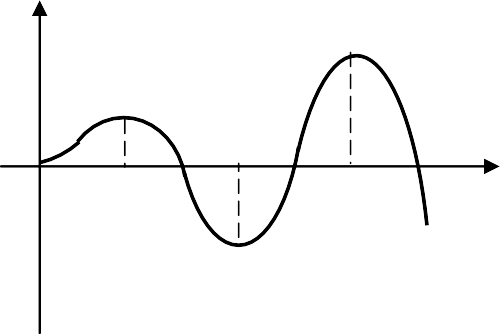
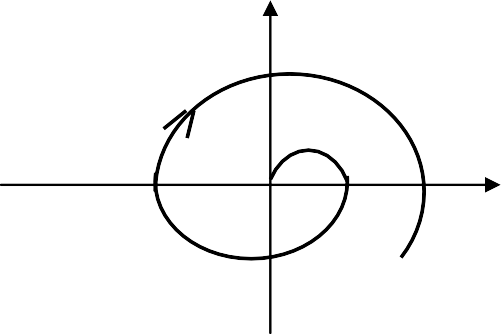
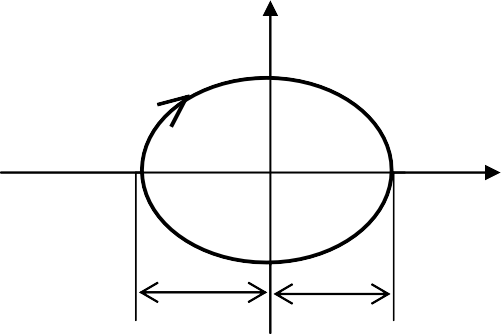
Фазовая траектория и переходный процесс однозначно соответ- ствуют друг другу на каждом элементарном участке на основании со- отношения y=dx/dt≈∆x/∆t. На рис. 4.2.2 показаны характерные фазо- вые траектории для свободных движений в САУ второго порядка, со- ответствующие затухающему, расходящемуся и незатухающему ко- лебательным переходным процессам.
Из анализа кривых на рис. 4.2.2 вытекают следующие правила построения фазовых траекторий:
-
в верхней фазовой полуплоскости изображающая точка всегда движется слева направо в сторону увеличения координаты x, по- скольку скорость ее изменения положительна y=x′>0;
x y=х′x0 x=x0
t=0
0 t1 t2 t3 t4 t5 t t3 0 t5 t1 x
а б
х y=х′0 t0x
в г
х y=x′
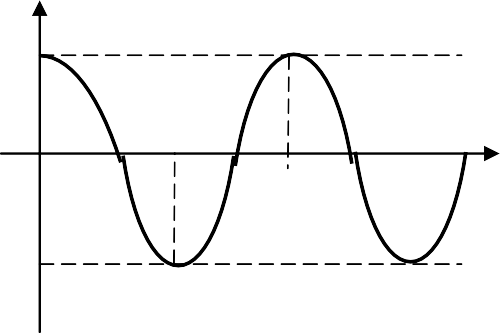хм0 tx
хм xм
д е
Рис. 4.2.2. Переходные процессы и фазовые траектории нелинейной системы второго порядка
-
в нижней фазовой полуплоскости, наоборот, изображающая точка всегда движется справа налево; -
фазовые траектории всегда пересекают ось абсцисс xпод пря- мым углом, так как при этом скорость y=x′=0, а величина xимеет максимальное или минимальное значения; -
затухающий колебательный процесс изображается на фазовой плоскости в виде спиралевидной кривой, сходящейся к точке поло- жения равновесия, а монотонный – в виде кривой, монотонно при- ближающейся к точке равновесия; -
расходящийся колебательный процесс изображается в виде расходящейся спиралевидной кривой, а монотонный – в виде моно- тонно удаляющейся кривой; -
автоколебательный периодический процесс изображается на фазовой плоскости в виде замкнутой кривой, называемой предельным циклом, которую изображающая точка пробегает за время одного пе- риода колебаний.
Фазовый портрет нелинейной САУ, обладающей кусочно– линейной или разрывной нелинейной характеристикой, состоит из нескольких областей с различными фазовыми траекториями. Линии, отделяющие на фазовой плоскости одну область от другой, называ- ются линиями переключения. В точках пересечения фазовыми траек- ториями линий переключения происходит излом траекторий из-за изменения правой части уравнения (4.2.16).
Фазовые траектории обычно строят методом изоклин, не тре- бующим интегрирования уравнения (4.2.16). Изоклиной называют геометрическое место точек фазовой плоскости, в которых фазовые траектории имеют одинаковый угол наклона tgα=c=dy/dx=const.
Уравнение линии изоклины получается из (4.2.16) в виде
y F2 (x) /[c F1(x)],
(4.2.18)