Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 207
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 67∙0,005 = 0,335 м/с;
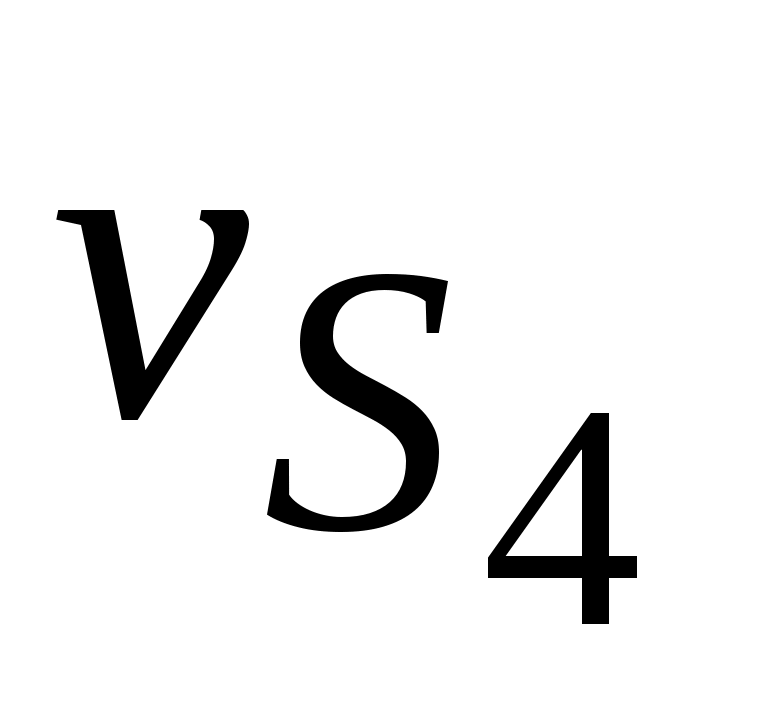 =
= 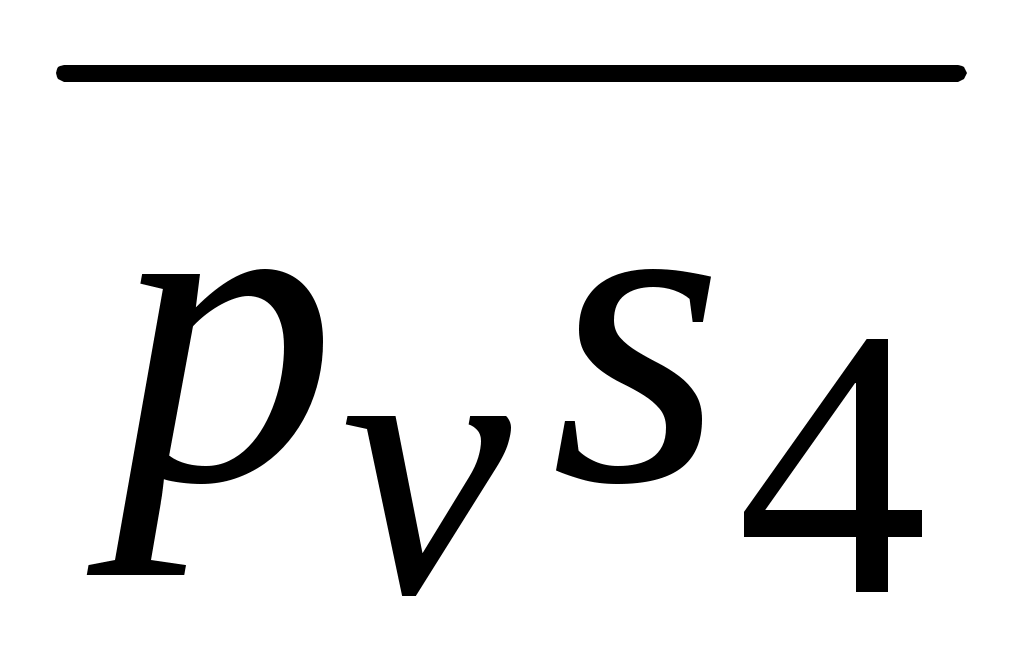 ∙μv = 62∙0,005 = 0,31 м/с;
∙μv = 62∙0,005 = 0,31 м/с;
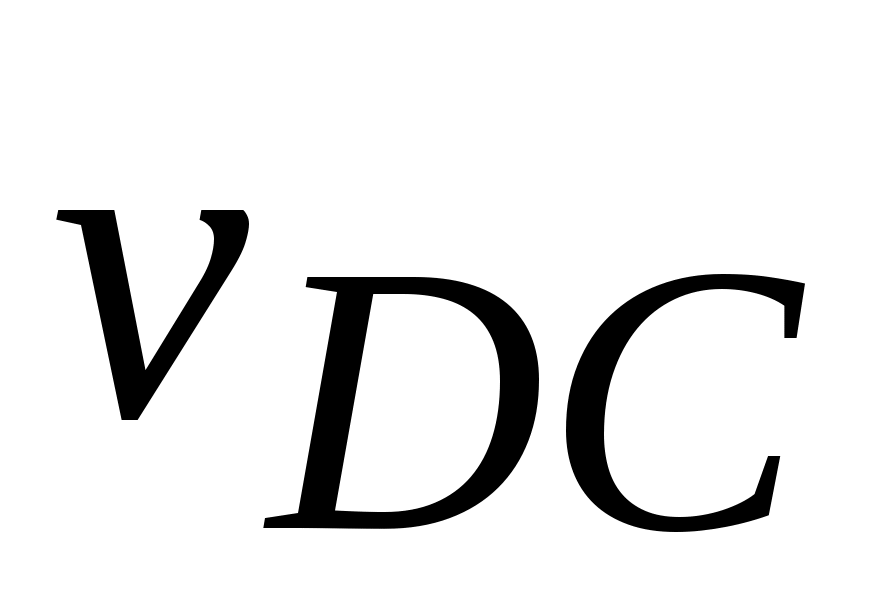 =
= 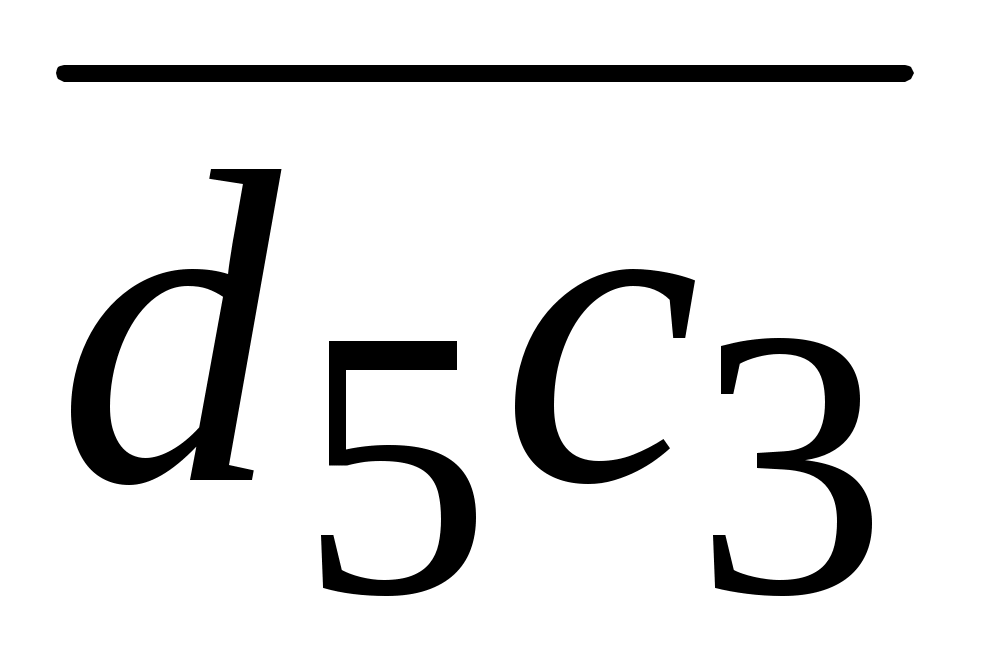 μv = 23∙0,005 = 0,115 м/с;
μv = 23∙0,005 = 0,115 м/с;
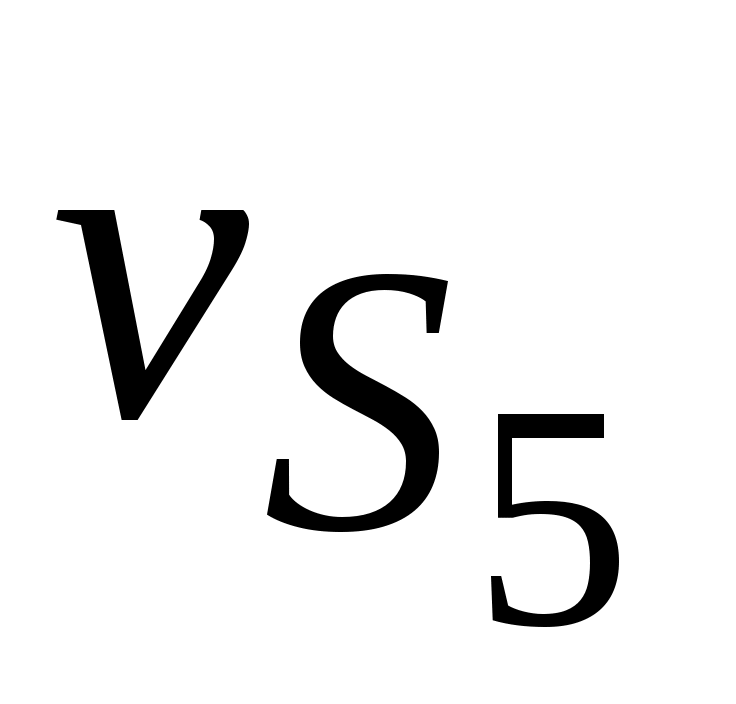 =
= 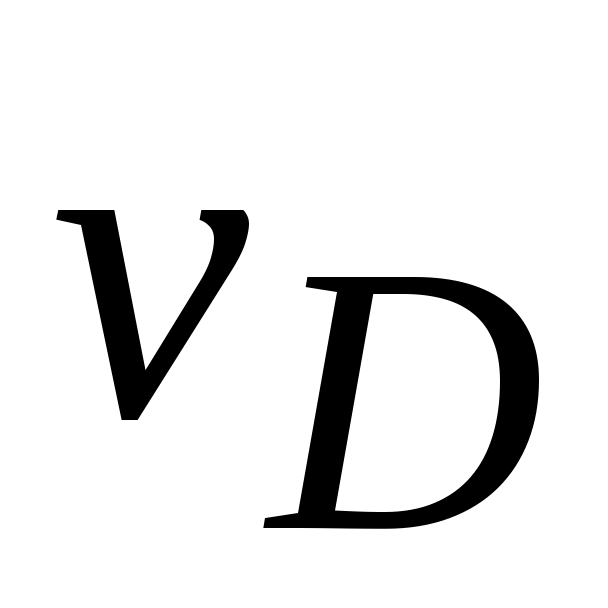 =
= 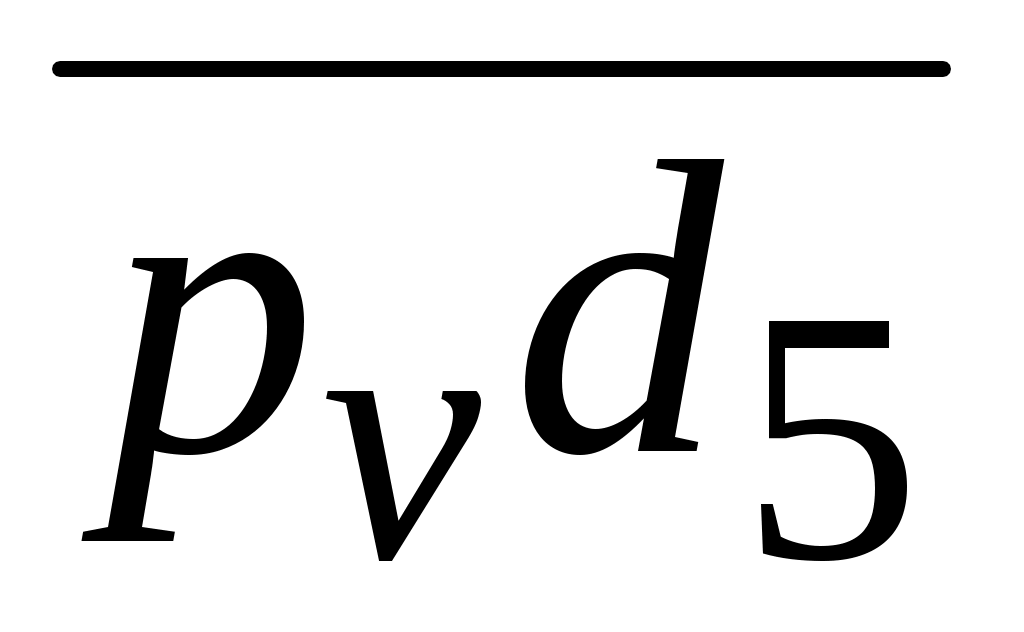 μv = 58∙0,005 = 0,29 м/с.
μv = 58∙0,005 = 0,29 м/с.
и угловых скоростей:
ω3 = /
/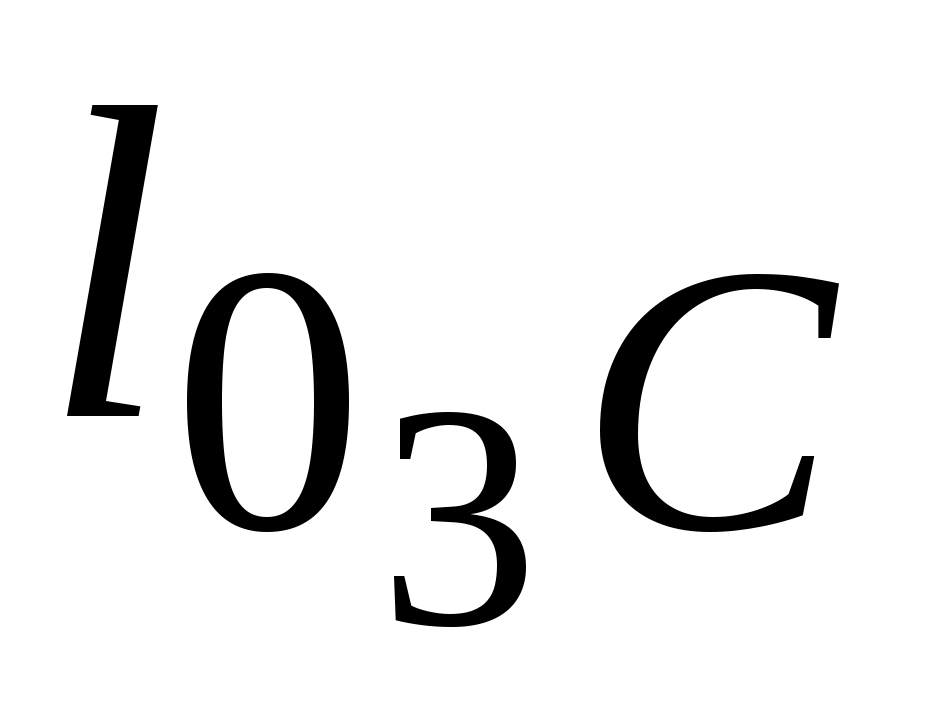 = 0,335/0,42 = 0,798 1/с;
= 0,335/0,42 = 0,798 1/с;
ω4 =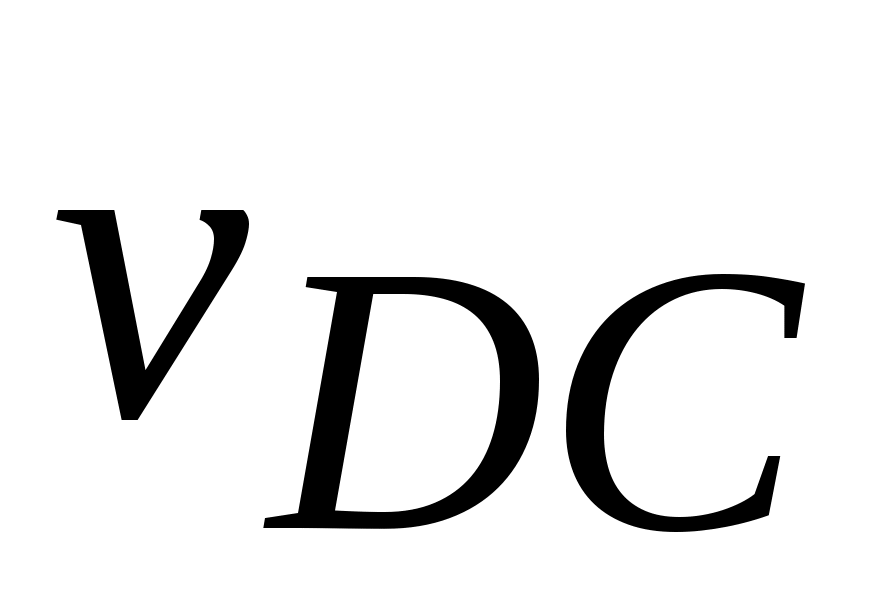 /lDC = 8,58/0,14 = 0,821 1/с.
/lDC = 8,58/0,14 = 0,821 1/с.
Пример 3
Схема механизма компрессора показана на рис. 2.10, а план скоростей изображен на рис. 2.11.
Задано: =60 об/мин. Угловая скорость
=60 об/мин. Угловая скорость
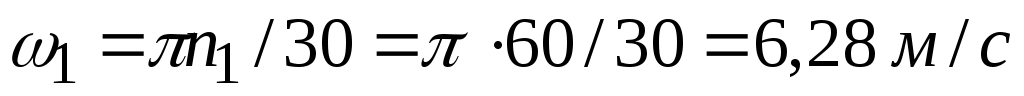 .
.
Скорость точки А, принадлежащей звеньям 1,2:
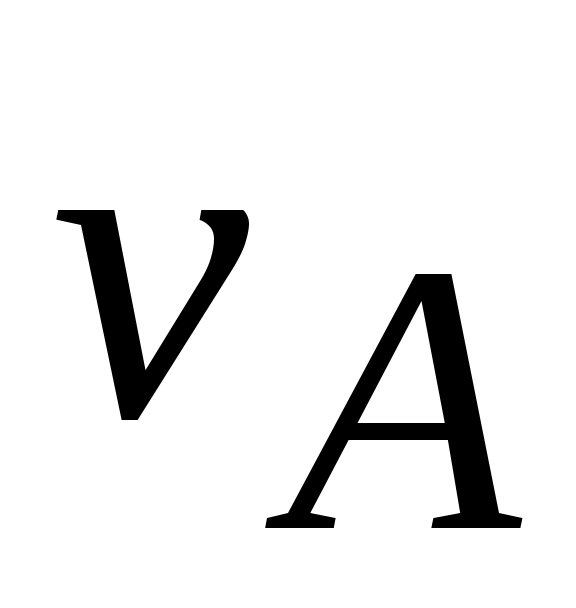 =
=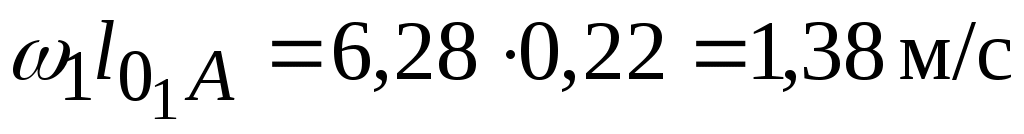 .
.
Задаемся длиной вектора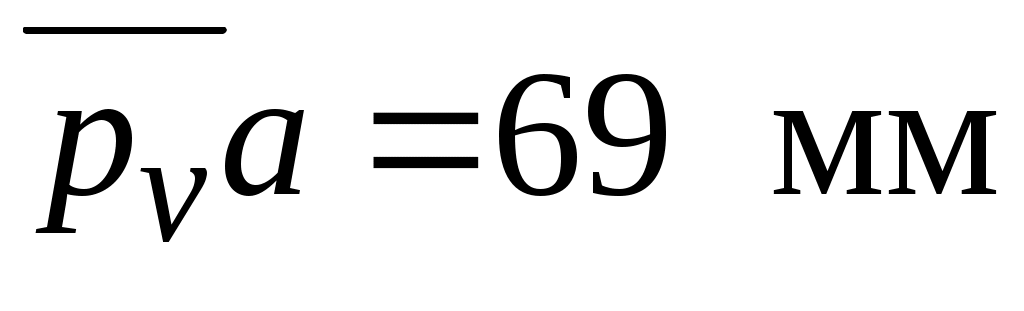 и находим
и находим
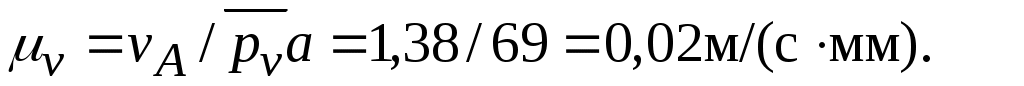
Из выбранной точки (полюс плана скоростей) проводим отрезок перпендикулярно положению кривошипа О1А (рис. 2.11) в направлении
(полюс плана скоростей) проводим отрезок перпендикулярно положению кривошипа О1А (рис. 2.11) в направлении  . Для точки В, принадлежащей одновременно двум звеньям 2 и 3, векторное уравнение запишем:
. Для точки В, принадлежащей одновременно двум звеньям 2 и 3, векторное уравнение запишем:
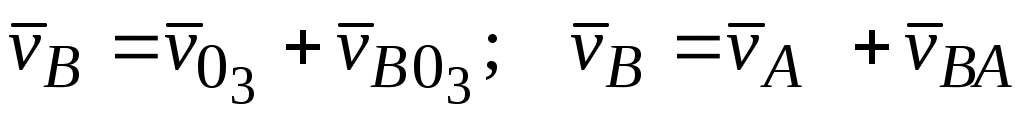
или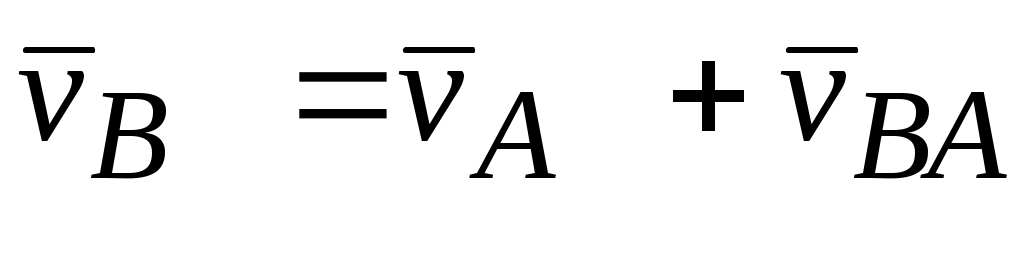
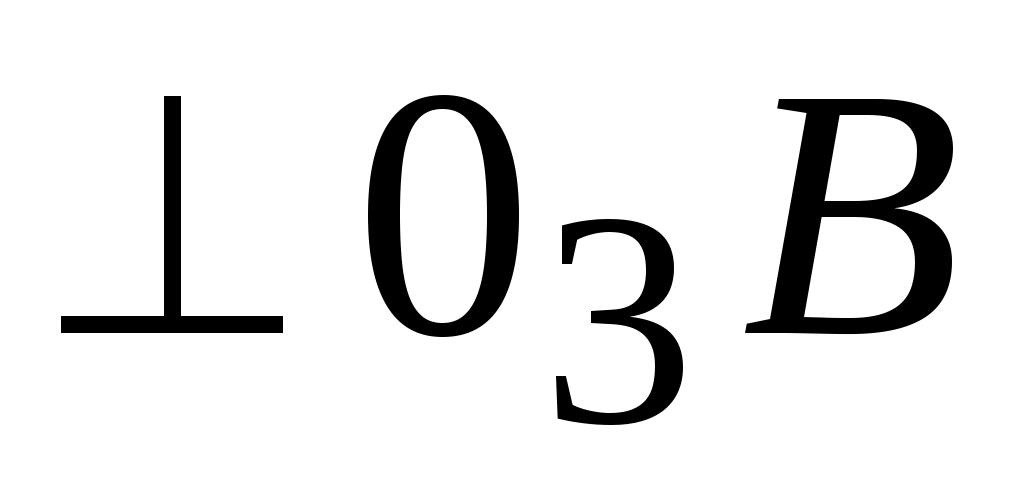
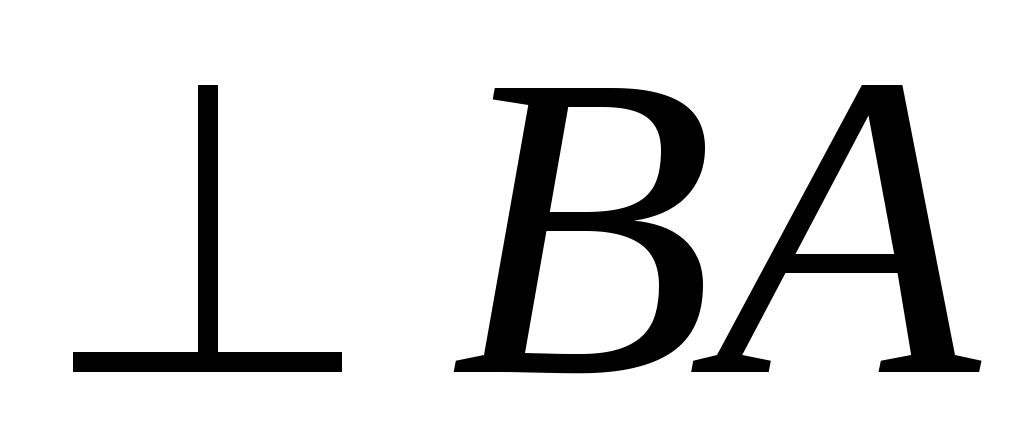
Решаем это уравнение графически (рис. 2.13). Через точку проводим прямую, перпендикулярную звену АВ, а из полюса – прямую, перпендикулярную О3В. Пересечение прямых определяет положение точки
проводим прямую, перпендикулярную звену АВ, а из полюса – прямую, перпендикулярную О3В. Пересечение прямых определяет положение точки . Точка с принадлежит 3-ему звену (треугольник ВО3С). Такой же треугольник (подобный) построим на плане скоростей
. Точка с принадлежит 3-ему звену (треугольник ВО3С). Такой же треугольник (подобный) построим на плане скоростей 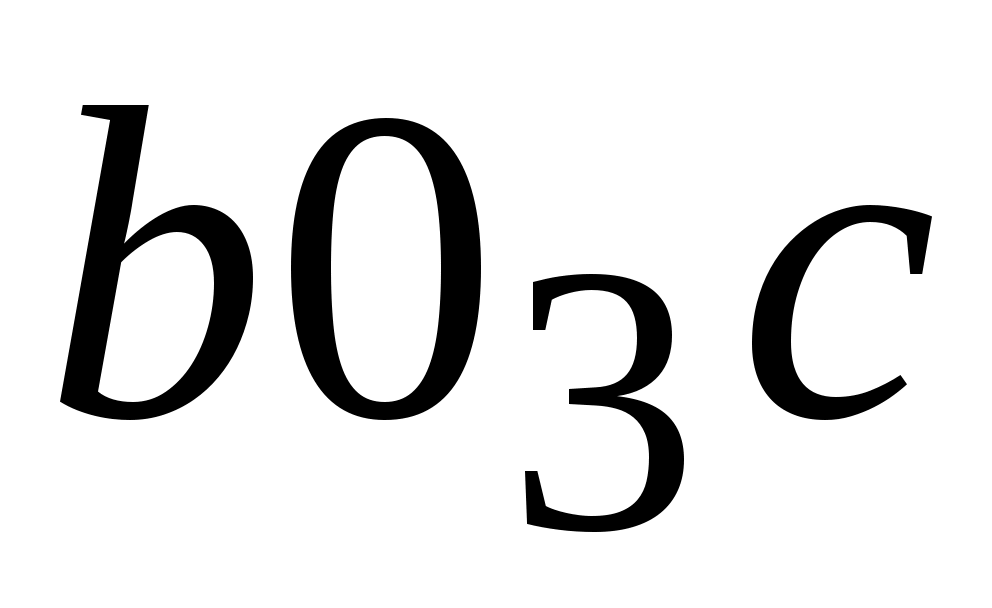 . Векторные уравнения для определения скорости точки D будут
. Векторные уравнения для определения скорости точки D будут
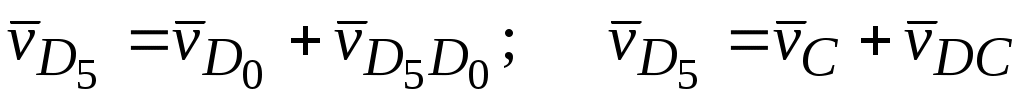 ,
, 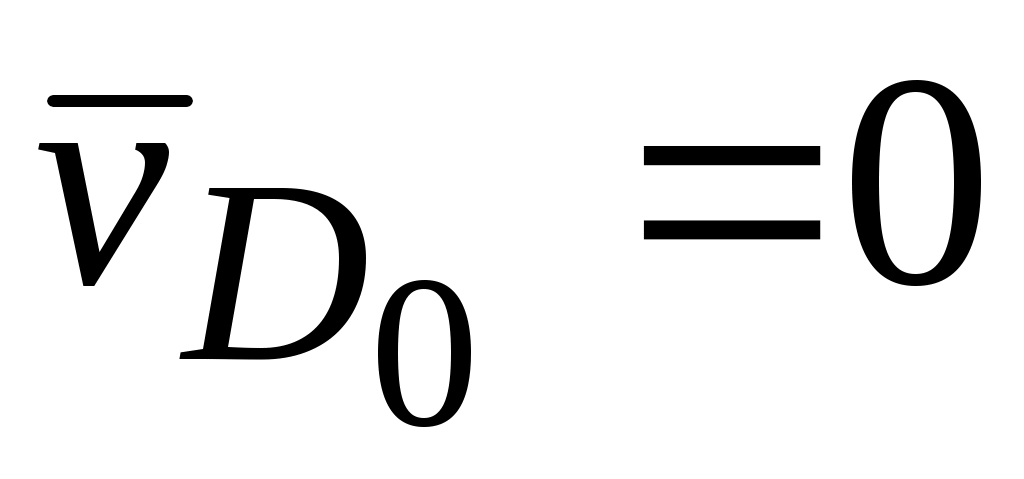 или
или
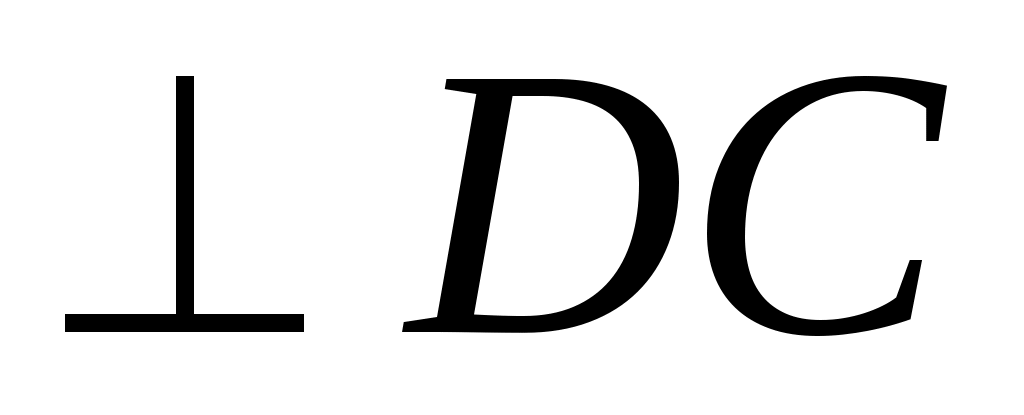
Из точки c проводим прямую, перпендикулярную DC, а через полюс – прямую, параллельную оси у. Пересечение определяет точку d. Скорости центров масс S2, S4 находим по свойству пропорциональности. Концы векторов расположены в середине векторов. Точки, скорости которых равны нулю, находятся в полюсе. Скорости точек и угловые скорости звеньев определяем аналогично 2-му примеру.
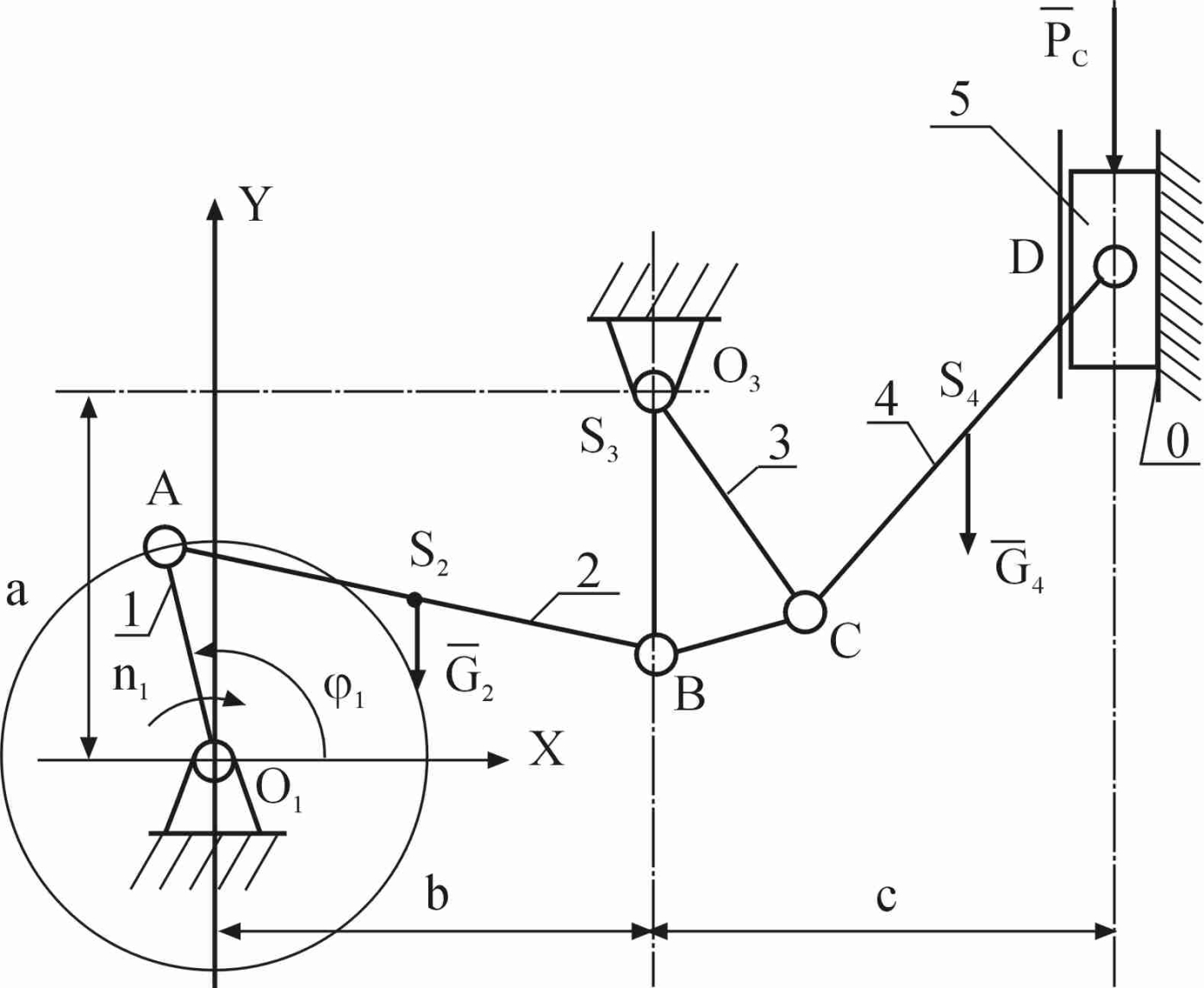
Рис. 2.10. Схема механизма
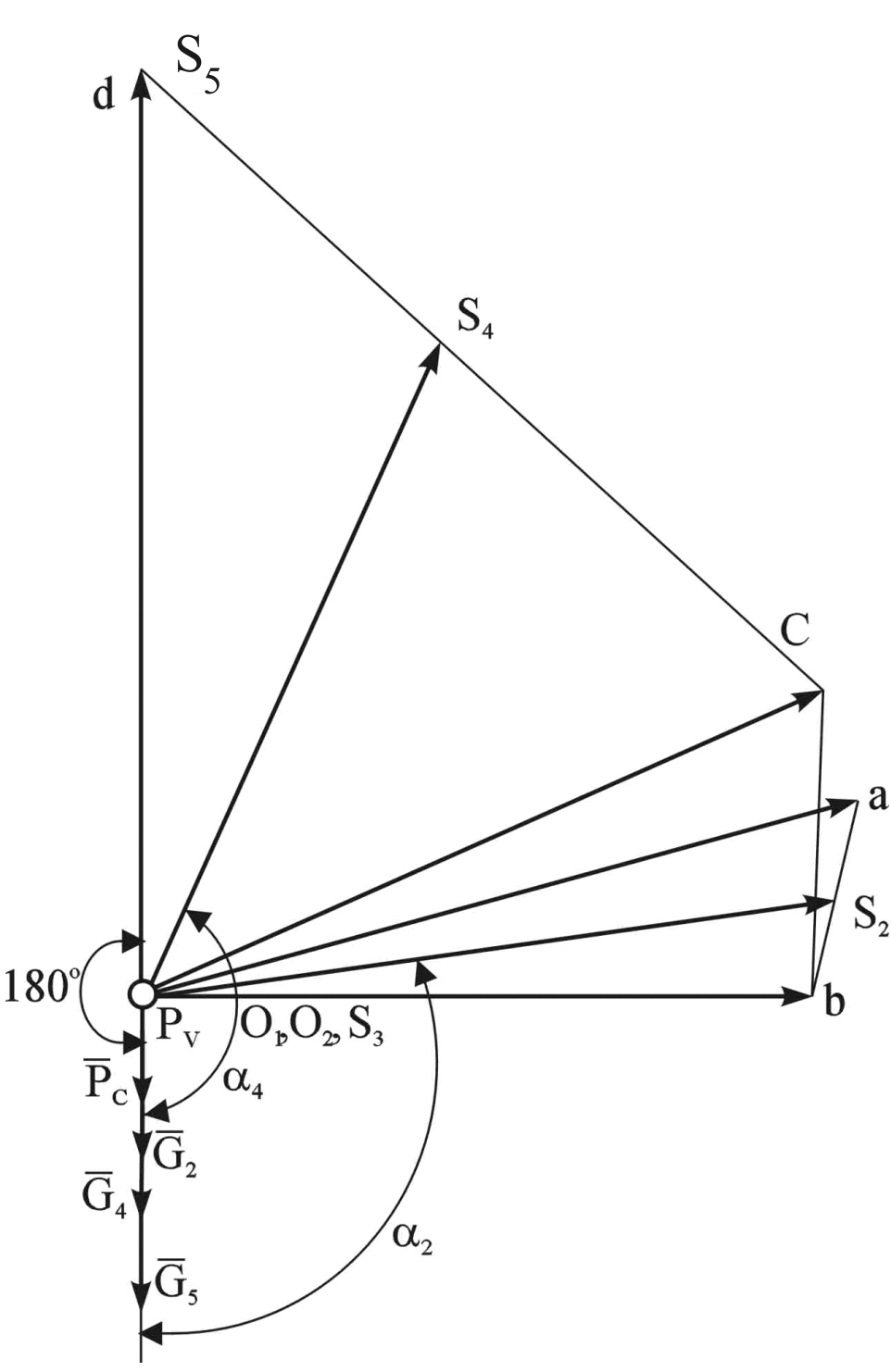
Рис. 2.11. План скоростей
Построение плана ускорений рассмотрим на примере брикетировочного автомата (схемы кулисного механизма) и компрессора (механизм без кулисных пар).
Брикетировочный автомат (рис. 2.7). Точка А одновременно принадлежит звеньям 1,2 и 3. Ускорение точки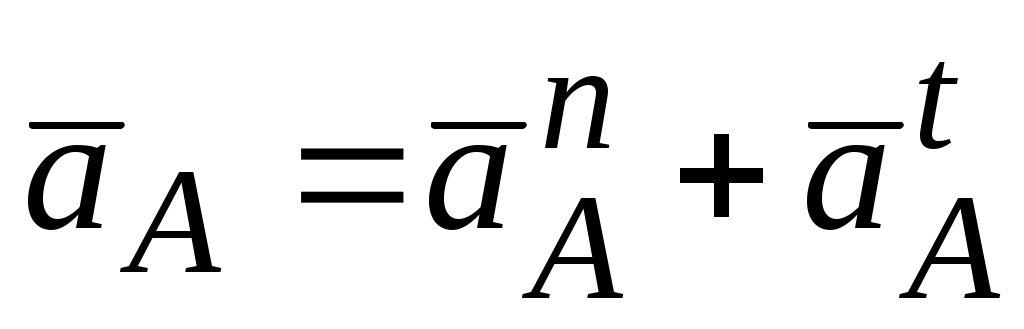 . Начальное звено (1) – кривошип вращается с постоянной угловой скоростью, поэтому составляющая
. Начальное звено (1) – кривошип вращается с постоянной угловой скоростью, поэтому составляющая 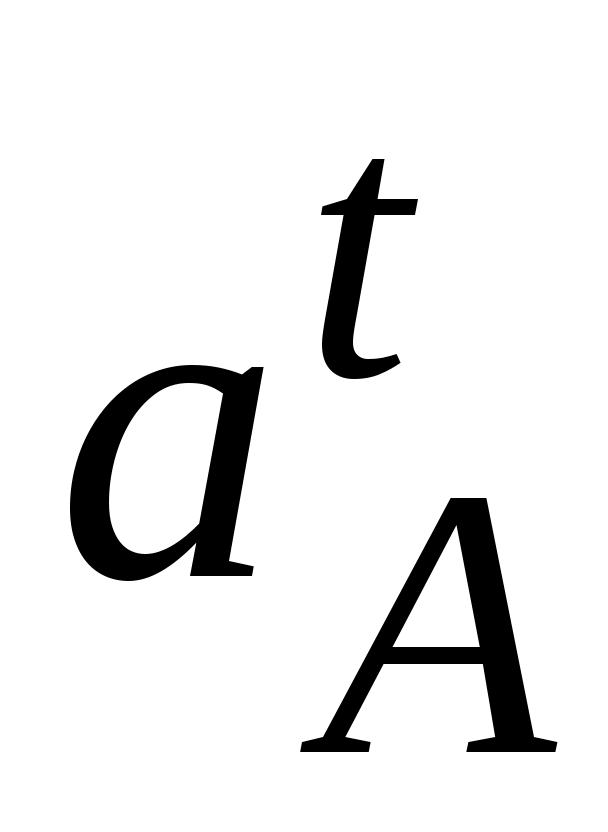 = 0, и
= 0, и 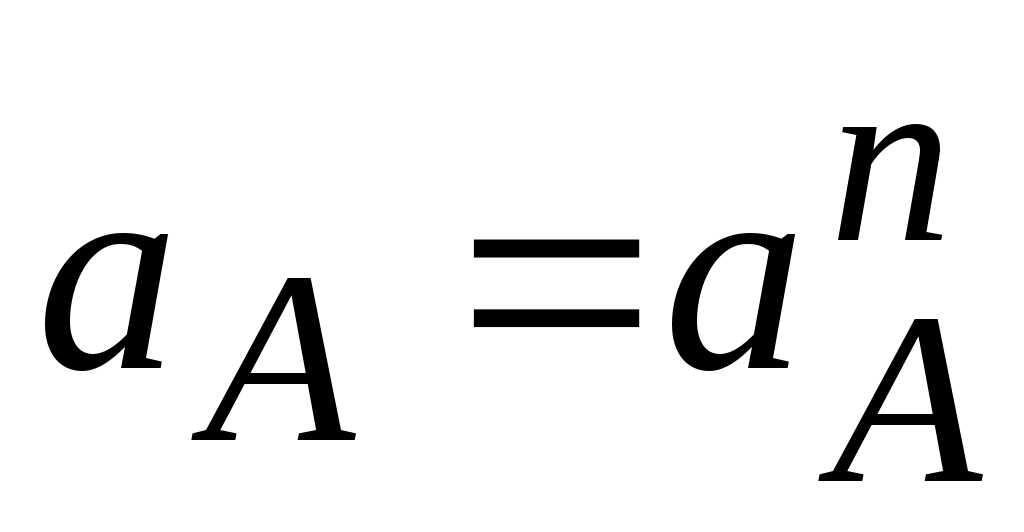
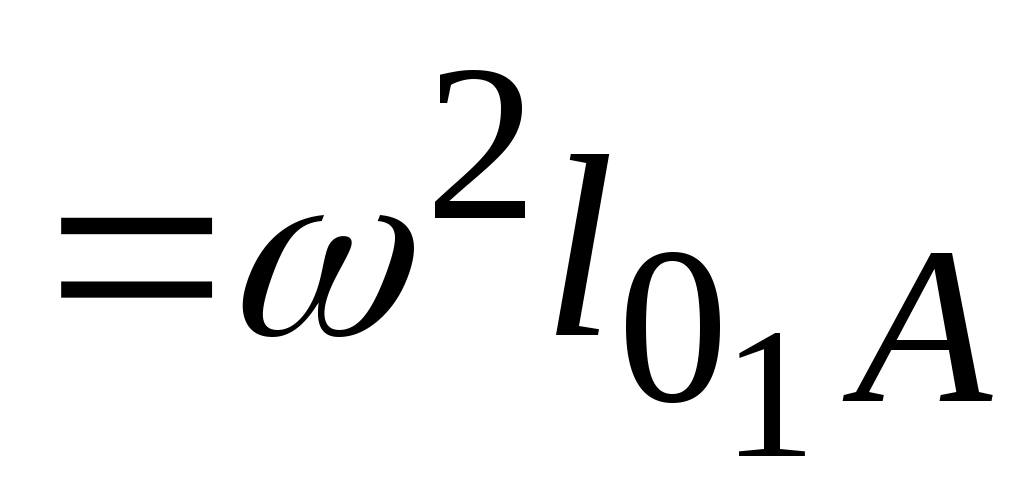 = 4,182∙0,08 = 1,4 м/с2. Масштабный коэффициент плана ускорений
= 4,182∙0,08 = 1,4 м/с2. Масштабный коэффициент плана ускорений 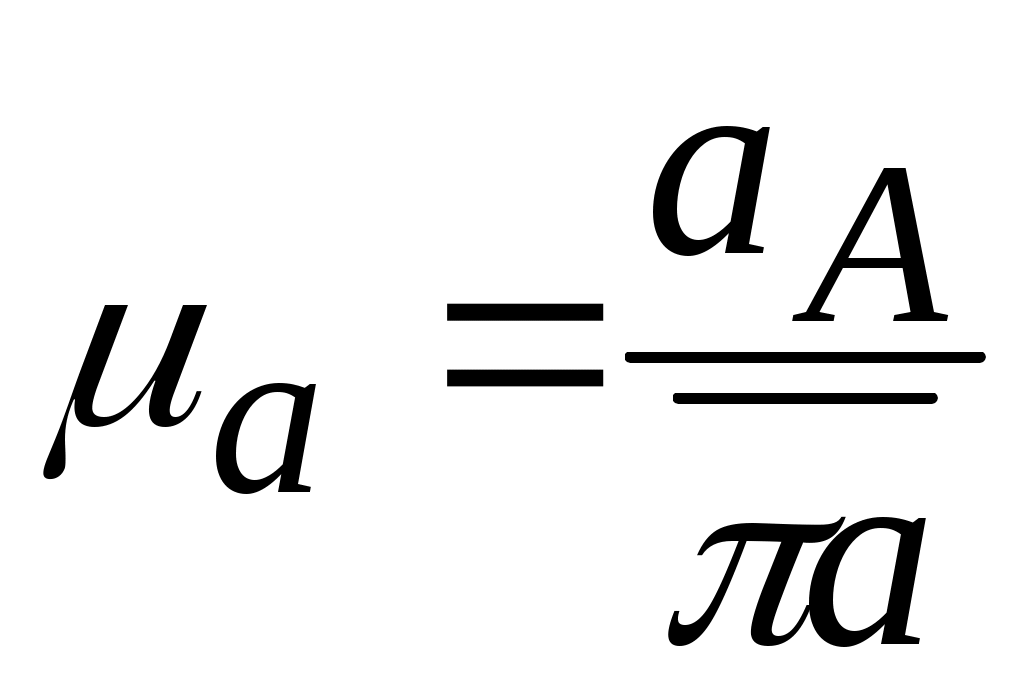 . Задаем
. Задаем  = 70 мм, тогда
= 70 мм, тогда
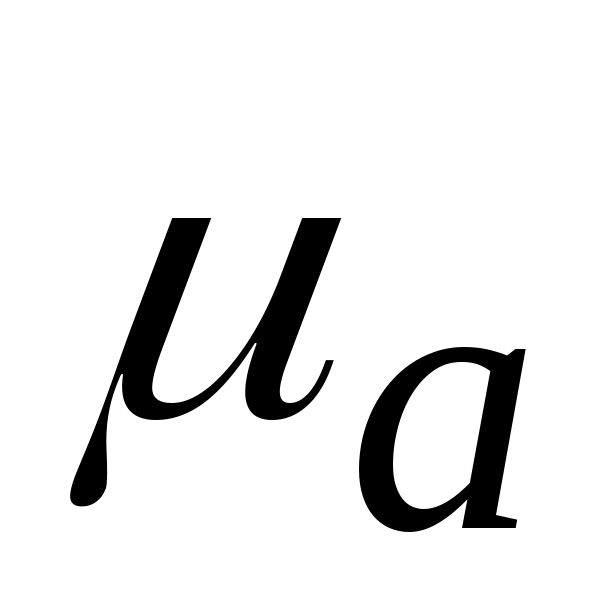 =
= 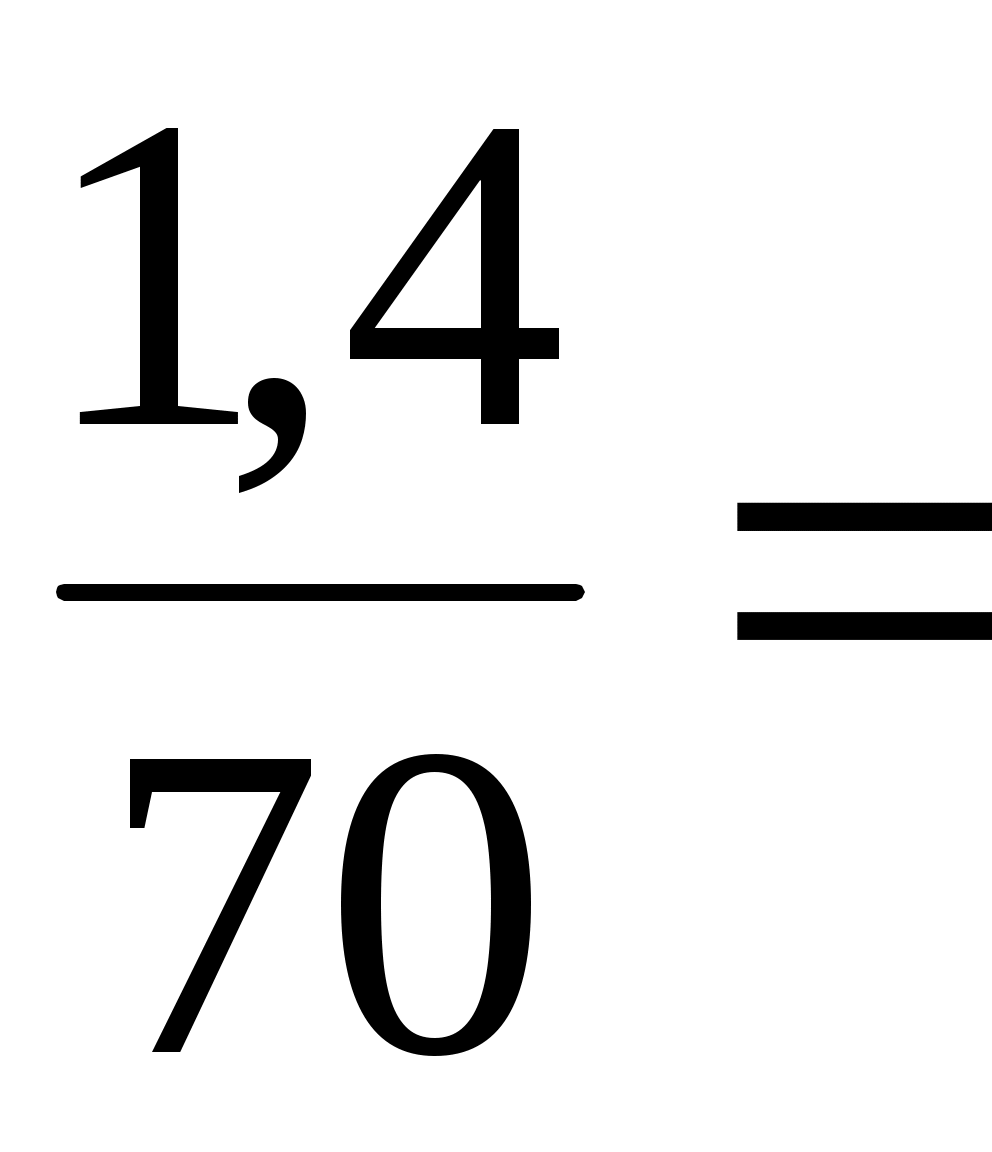 0,02 (м/с2 )/ мм.
0,02 (м/с2 )/ мм.
Из произвольно выбранной точки на чертеже (π – полюс плана) откладываем нормальную составляющую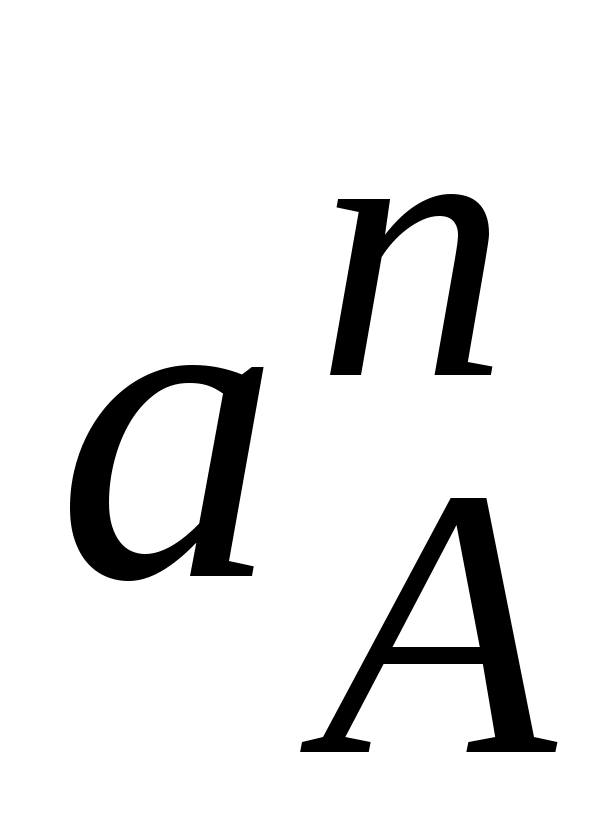

 в виде 70 мм, направленную к центру вращения кривошипа 01 (рис.2.12). Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны
в виде 70 мм, направленную к центру вращения кривошипа 01 (рис.2.12). Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны 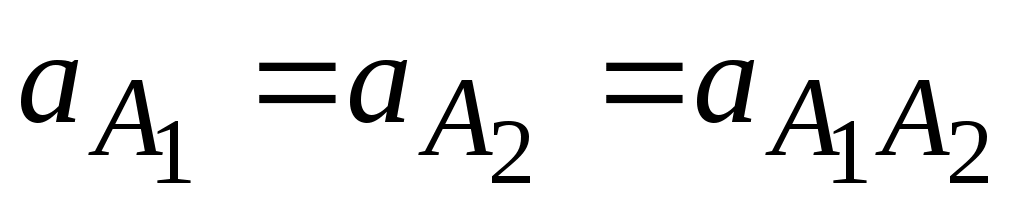 .
.
Поскольку переносное движение вращательное, имеем следующее векторное уравнение

 =
= 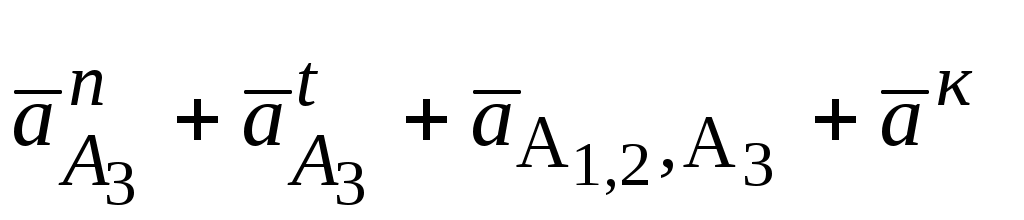 , ( * )
, ( * )
где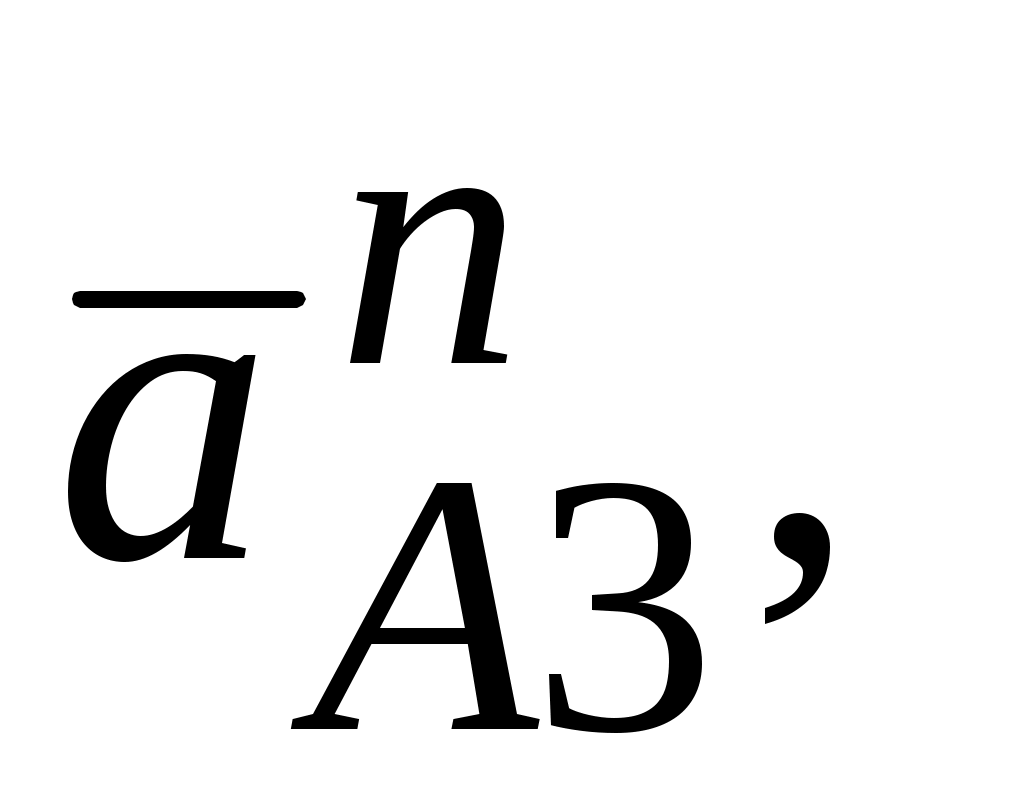
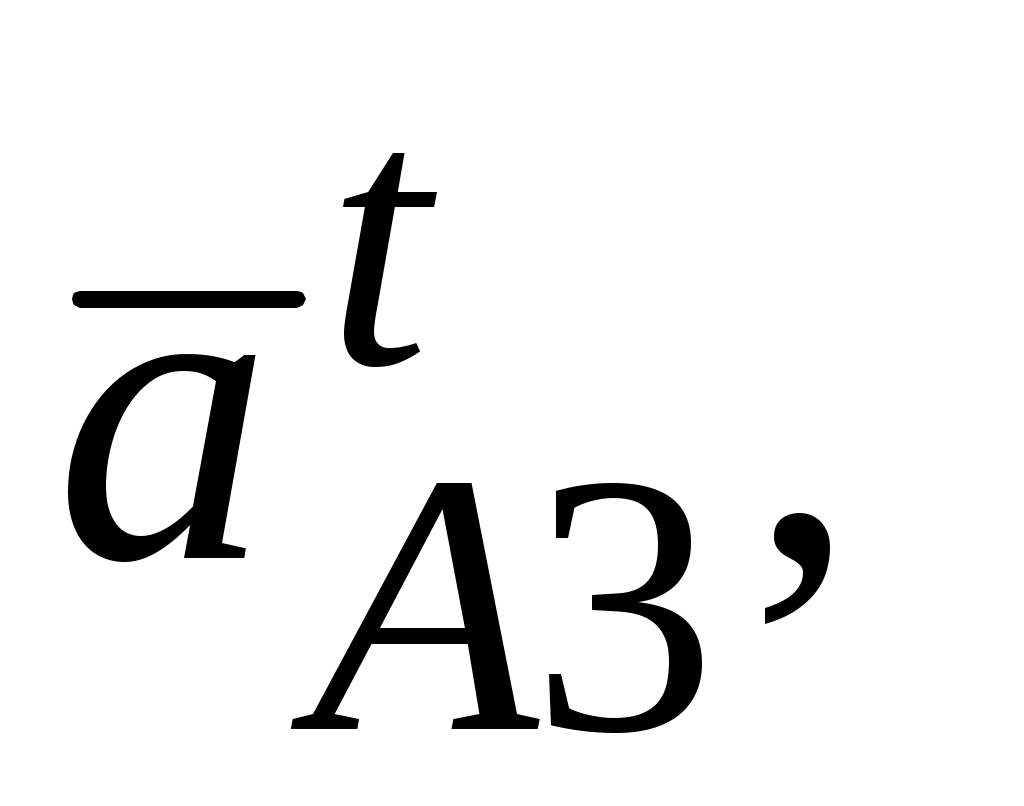 – соответственно нормальная и тангенциальная составляющие переносного движения для точки
– соответственно нормальная и тангенциальная составляющие переносного движения для точки 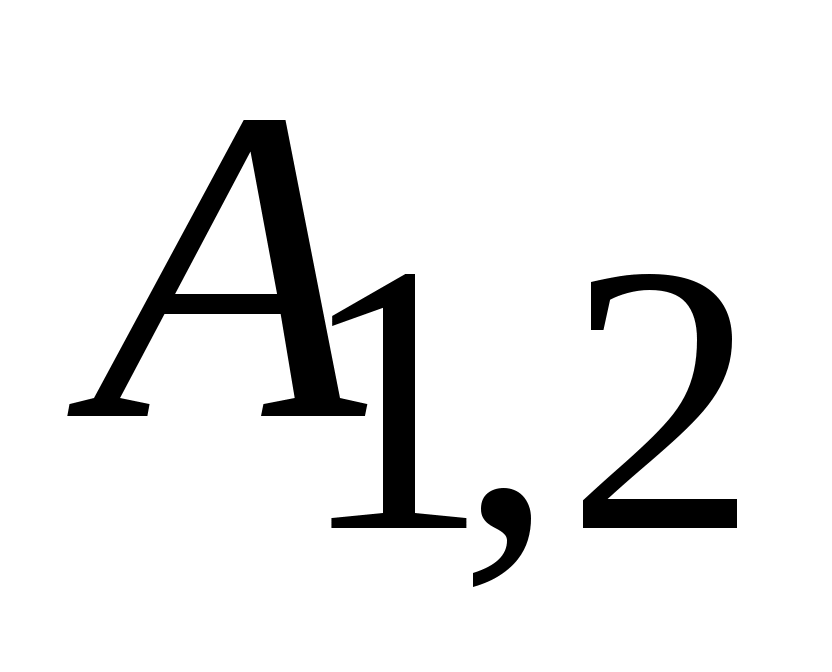 , которое является абсолютным для точки
, которое является абсолютным для точки (рис.2.10). Ускорение
(рис.2.10). Ускорение 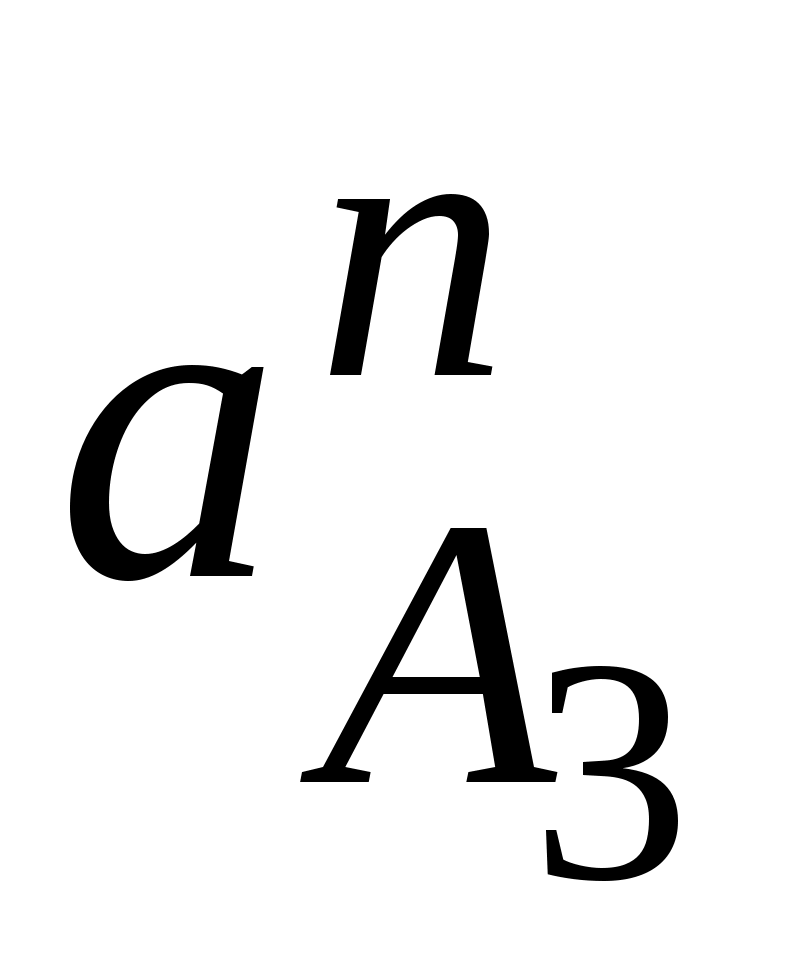 =
= 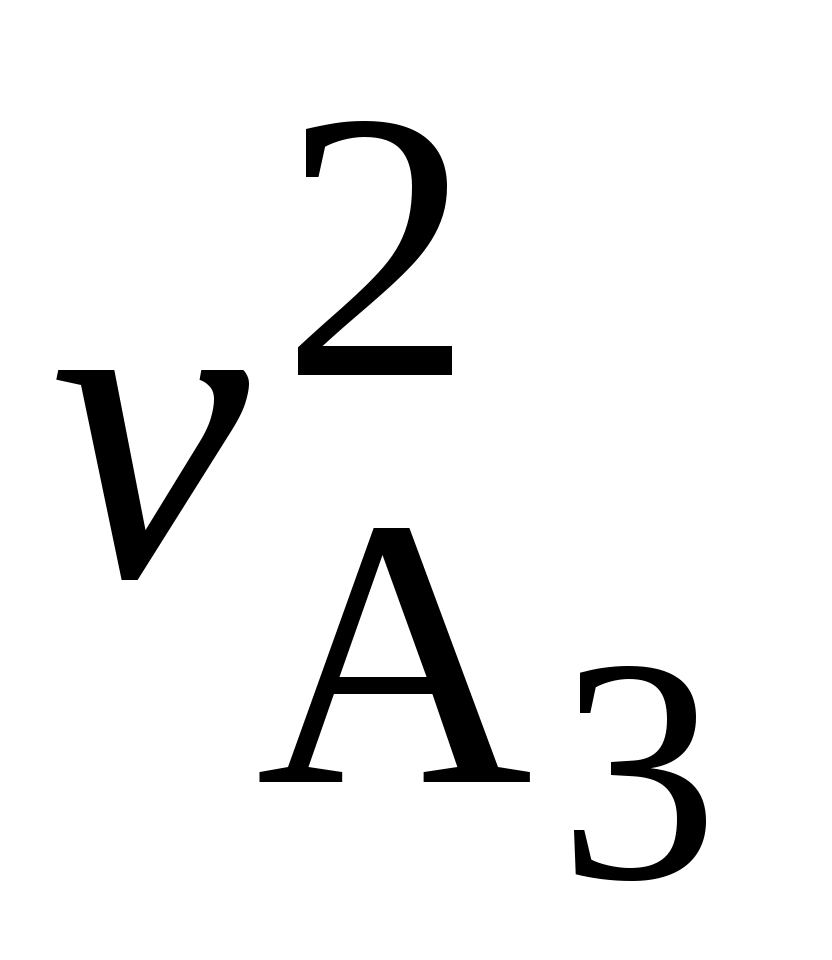 /
/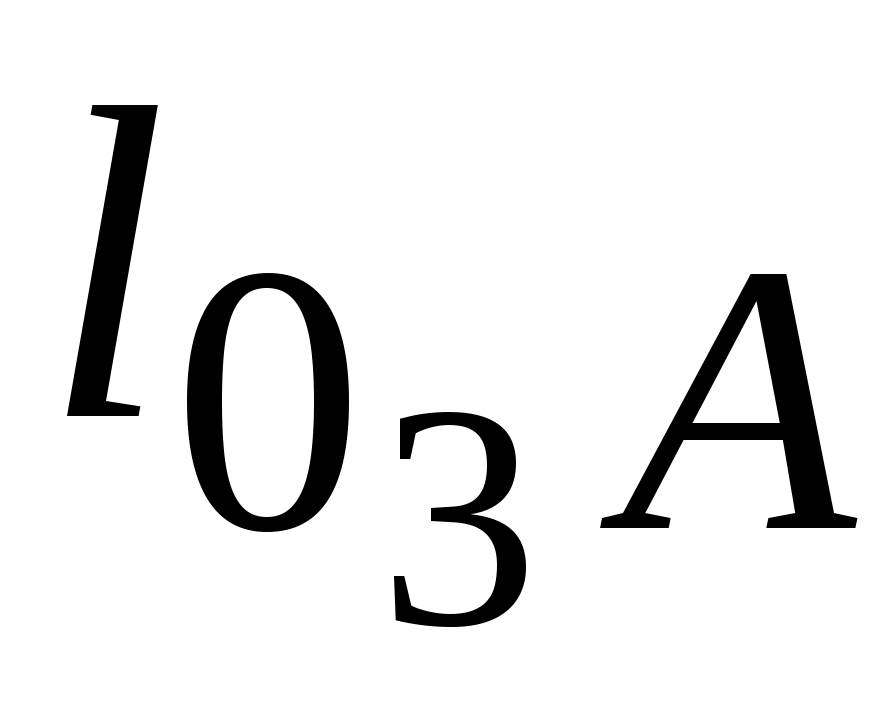 , а
, а 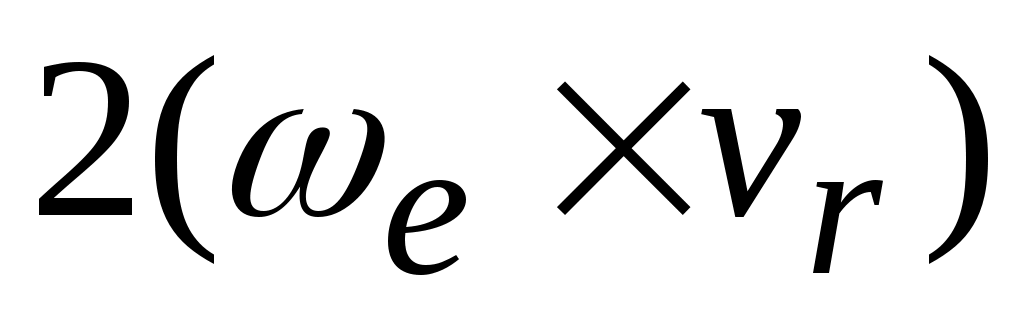 =
= 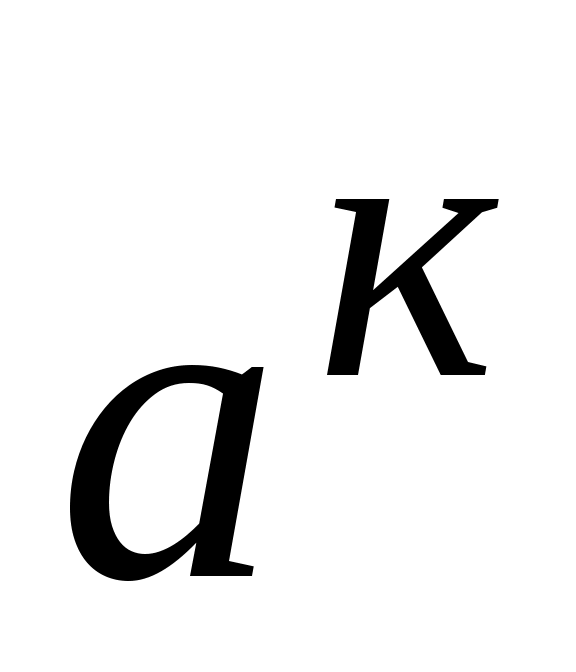
– поворотное ускорение точки (ускорение Кориолиса). Угловая скорость переносного движения
(ускорение Кориолиса). Угловая скорость переносного движения 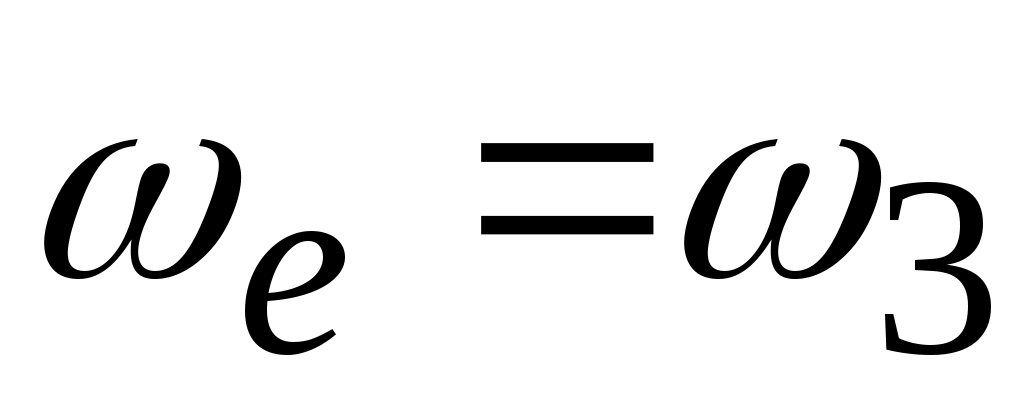 , а относительная скорость
, а относительная скорость 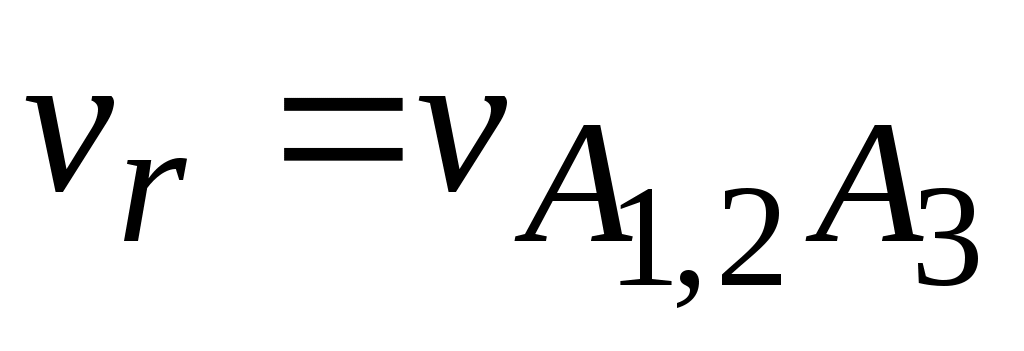 . Направление вектора
. Направление вектора  можно определить, если
можно определить, если 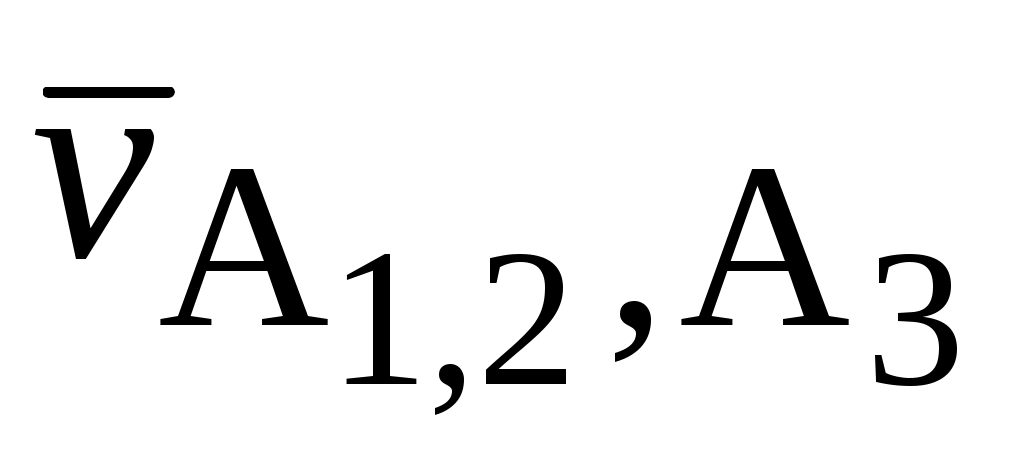 повернуть на 900 по направлению угловой скорости
повернуть на 900 по направлению угловой скорости 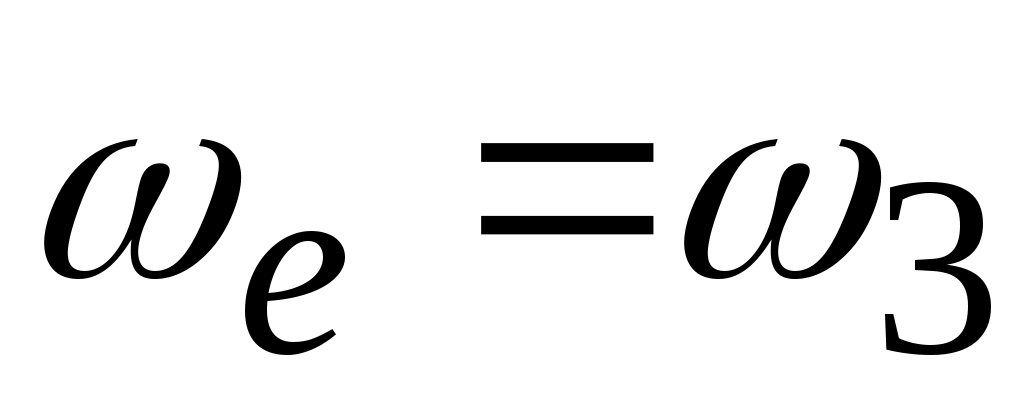 .
.
Согласно уравнению (*) строим вектор , перпендикулярно положению кулисы О3А и входящим в конец вектора
, перпендикулярно положению кулисы О3А и входящим в конец вектора 
 .. Через начало вектора
.. Через начало вектора  проводим направление
проводим направление 
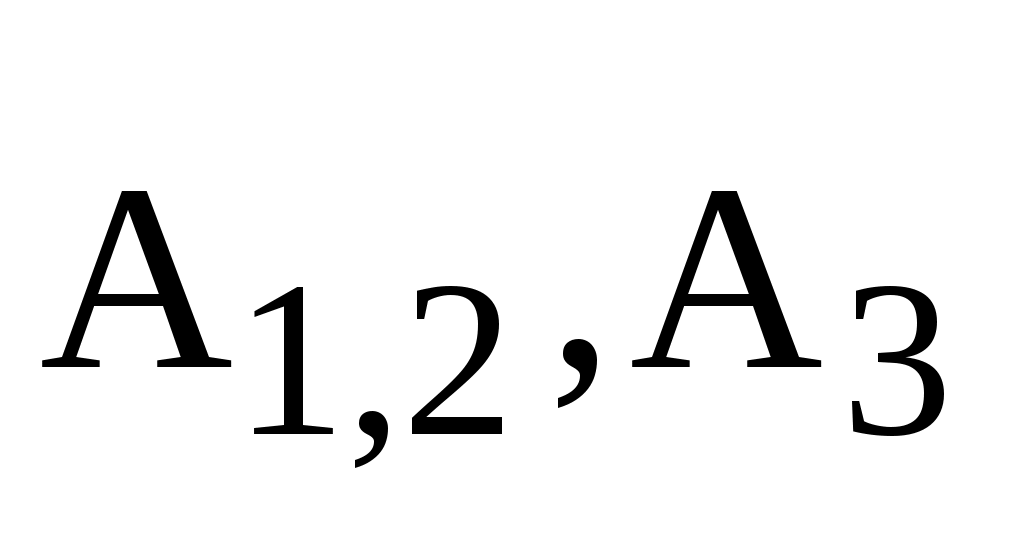 ||О3А. Далее из полюса
||О3А. Далее из полюса  проводим вектор
проводим вектор 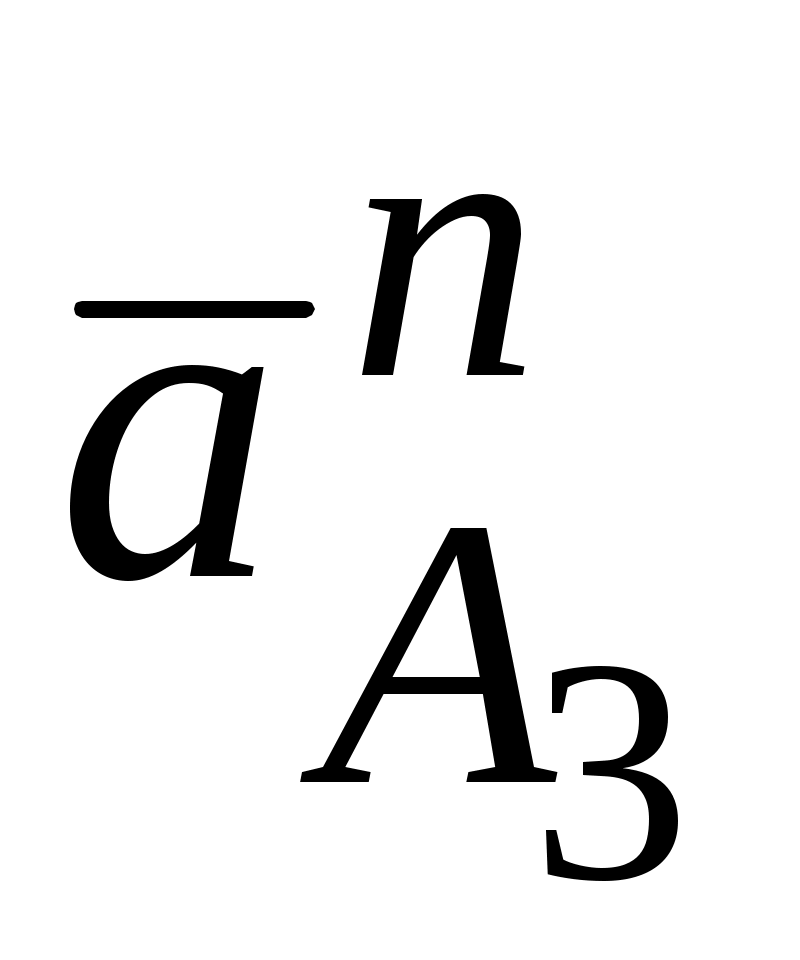 || О3А в направлении к т. О3, а из его конца направление вектора
|| О3А в направлении к т. О3, а из его конца направление вектора 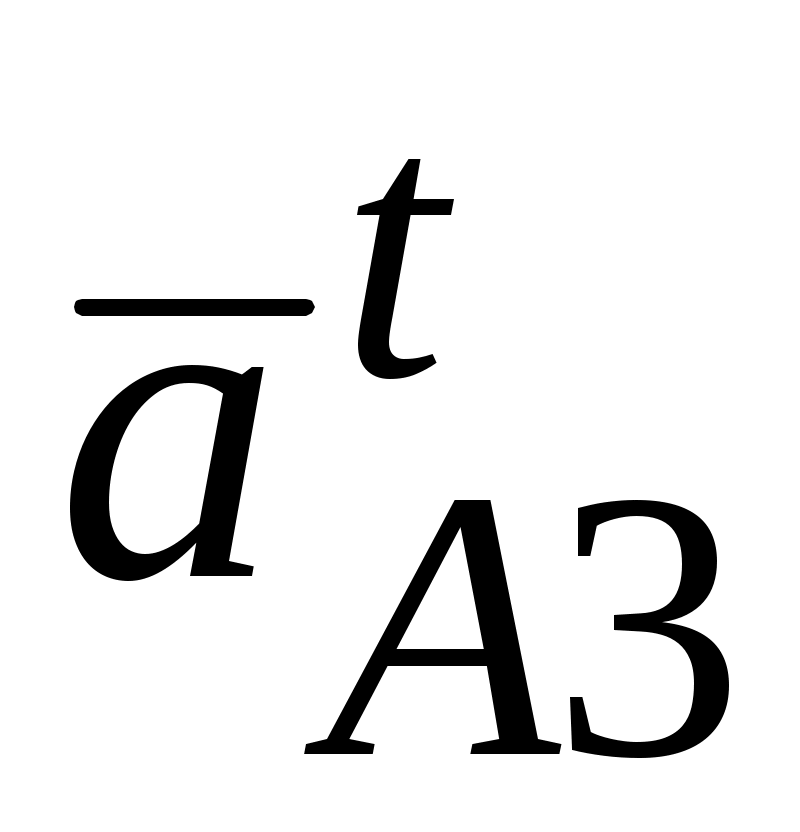
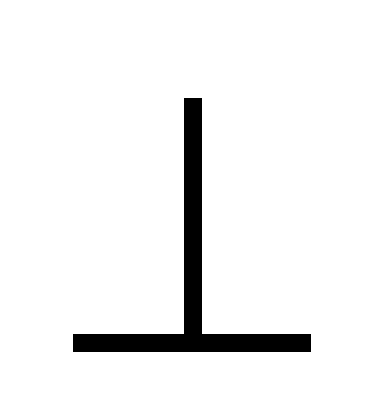 О3А до пересечения с направлением
О3А до пересечения с направлением 
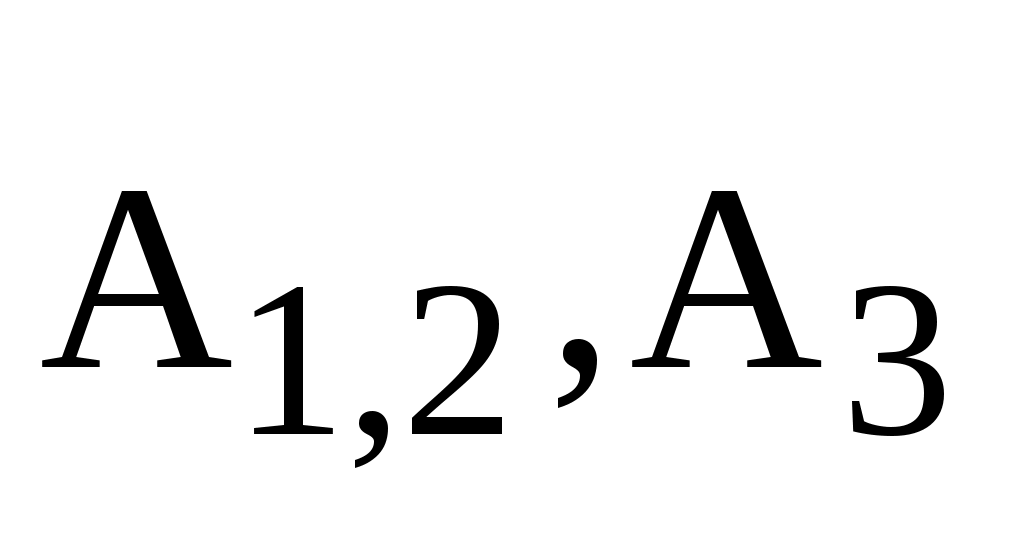 . Пересечение определяет положение точки
. Пересечение определяет положение точки 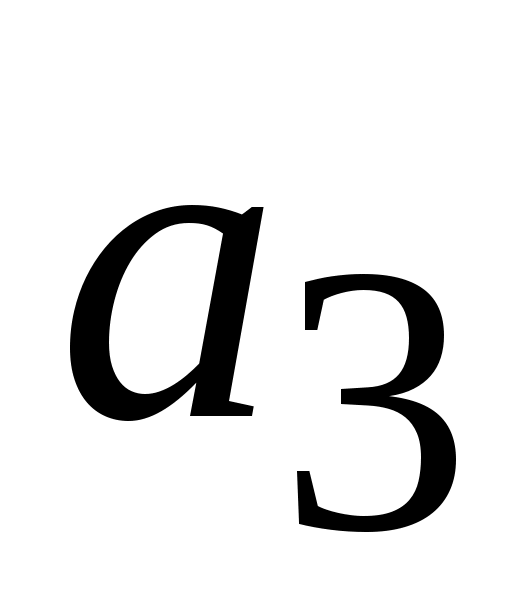 .
.
Положение точки на плане ускорений находим, как и при построении плана скоростей, по свойству подобия из условия
на плане ускорений находим, как и при построении плана скоростей, по свойству подобия из условия
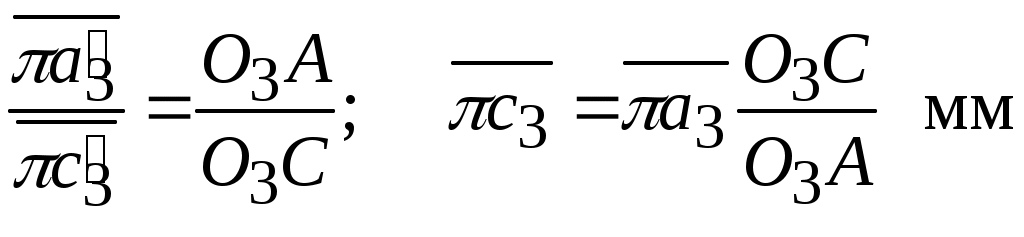 .
.
Для определения вектора ускорения точки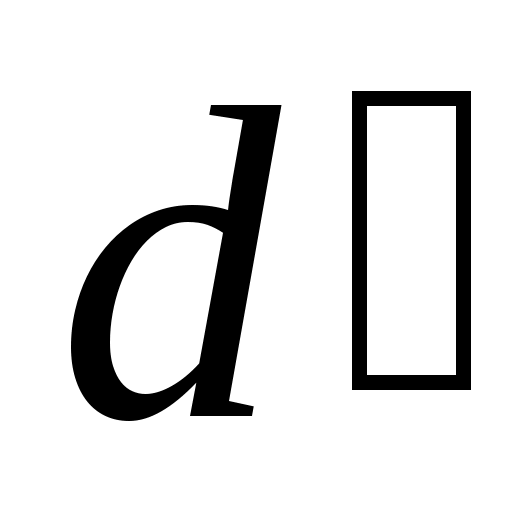 запишем уравнения:
запишем уравнения:
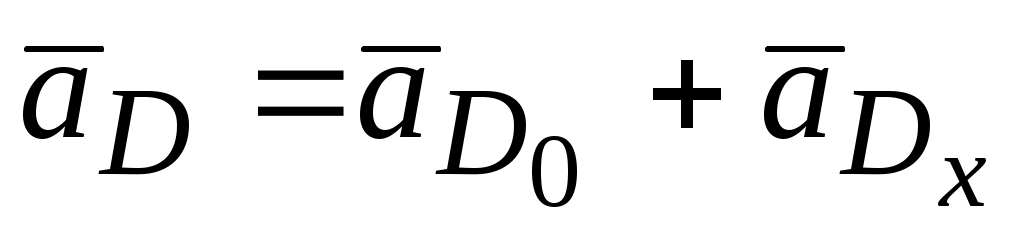 ;
; 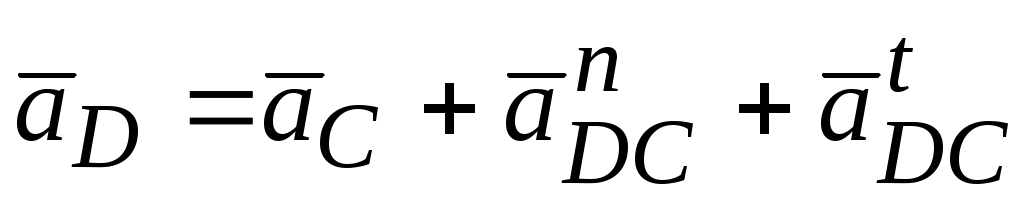 .
.
|| xx || DC DC
DC
Здесь
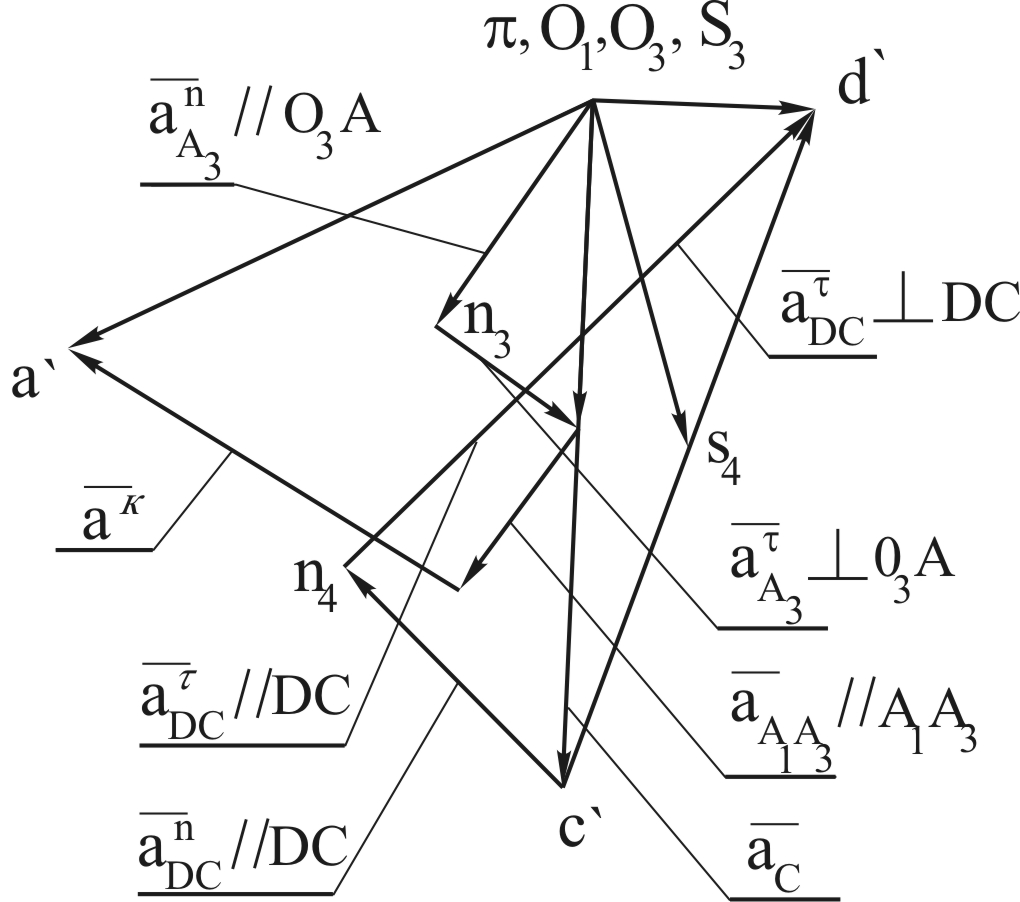
Рис.2.12. План ускорений механизма брикетировочного автомата
Рассмотрим построение плана ускорений для механизма компрессора (рис.2.10).
Начинаем с вычисления ускорения точки А, принадлежащей одновременно звеньям 1,2.
Для принятых исходных данных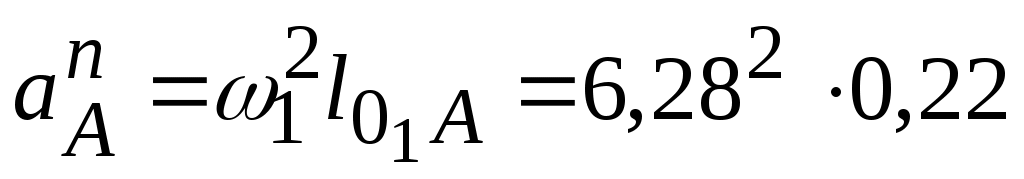 =8,7 м/с2. Выбираем
=8,7 м/с2. Выбираем 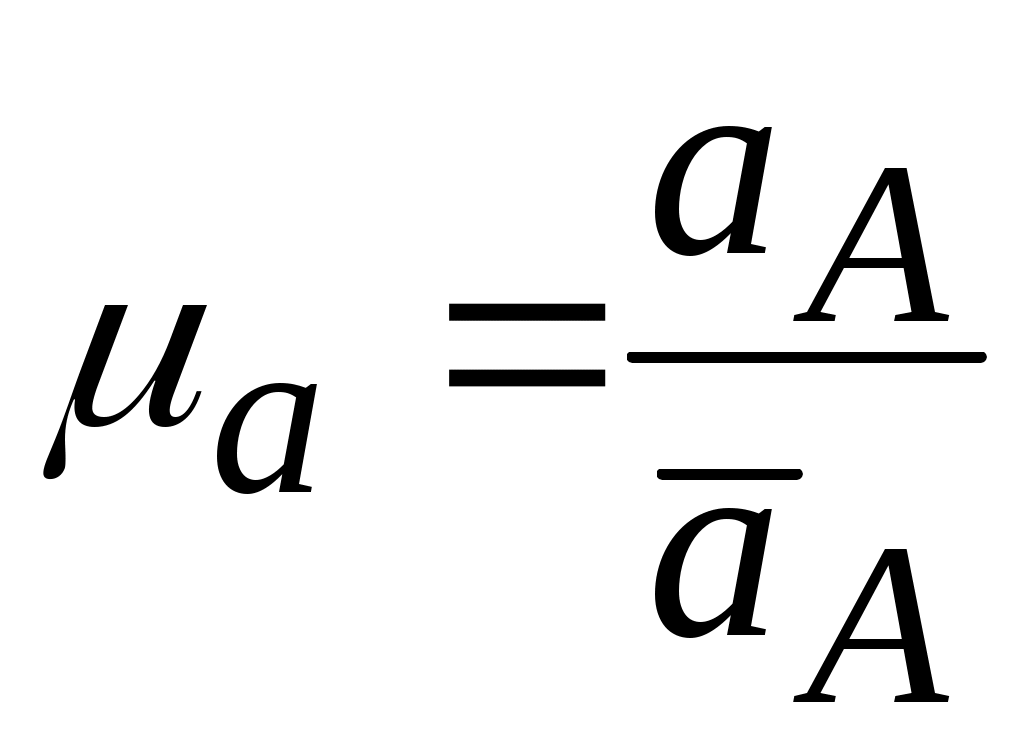 . Задаем
. Задаем 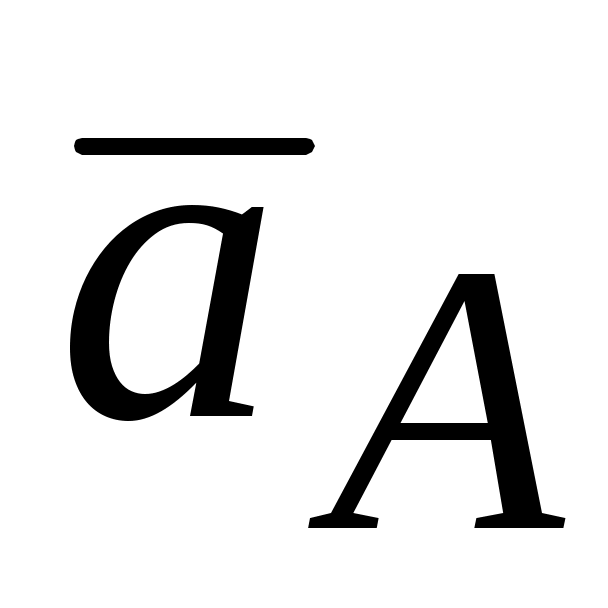
и угловых скоростей:
ω3 =
ω4 =
Пример 3
Схема механизма компрессора показана на рис. 2.10, а план скоростей изображен на рис. 2.11.
Задано:
Скорость точки А, принадлежащей звеньям 1,2:
Задаемся длиной вектора
Из выбранной точки
или
Решаем это уравнение графически (рис. 2.13). Через точку
Из точки c проводим прямую, перпендикулярную DC, а через полюс – прямую, параллельную оси у. Пересечение определяет точку d. Скорости центров масс S2, S4 находим по свойству пропорциональности. Концы векторов расположены в середине векторов. Точки, скорости которых равны нулю, находятся в полюсе. Скорости точек и угловые скорости звеньев определяем аналогично 2-му примеру.

Рис. 2.10. Схема механизма

Рис. 2.11. План скоростей
2.5. Примеры построения планов ускорений
Построение плана ускорений рассмотрим на примере брикетировочного автомата (схемы кулисного механизма) и компрессора (механизм без кулисных пар).
Брикетировочный автомат (рис. 2.7). Точка А одновременно принадлежит звеньям 1,2 и 3. Ускорение точки
Из произвольно выбранной точки на чертеже (π – полюс плана) откладываем нормальную составляющую
Поскольку переносное движение вращательное, имеем следующее векторное уравнение
где
– поворотное ускорение точки
Согласно уравнению (*) строим вектор
Положение точки
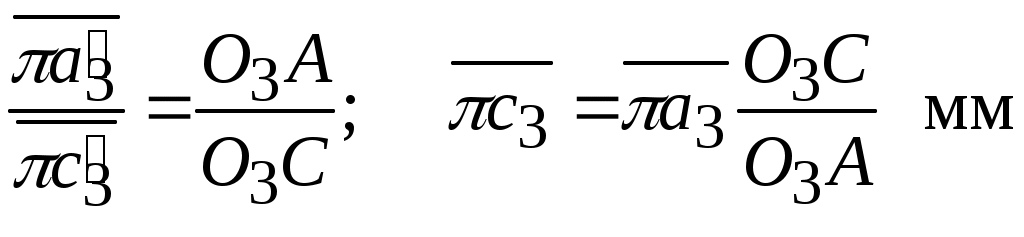 .
.Для определения вектора ускорения точки
|| xx || DC
Здесь 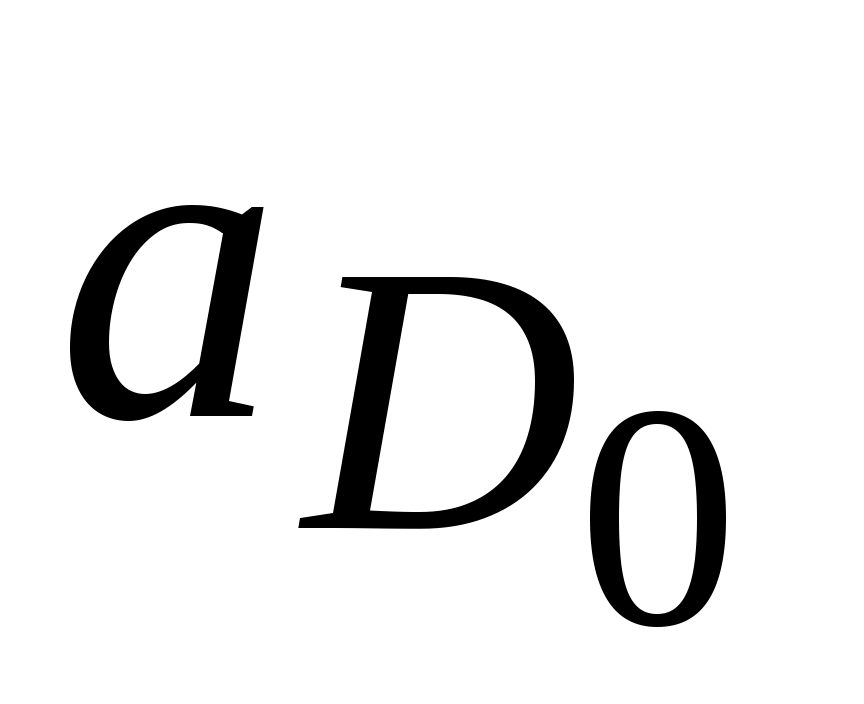 = 0. Решаем последние векторные уравнения. Из точки с′
= 0. Решаем последние векторные уравнения. Из точки с′
проводим величину вектора 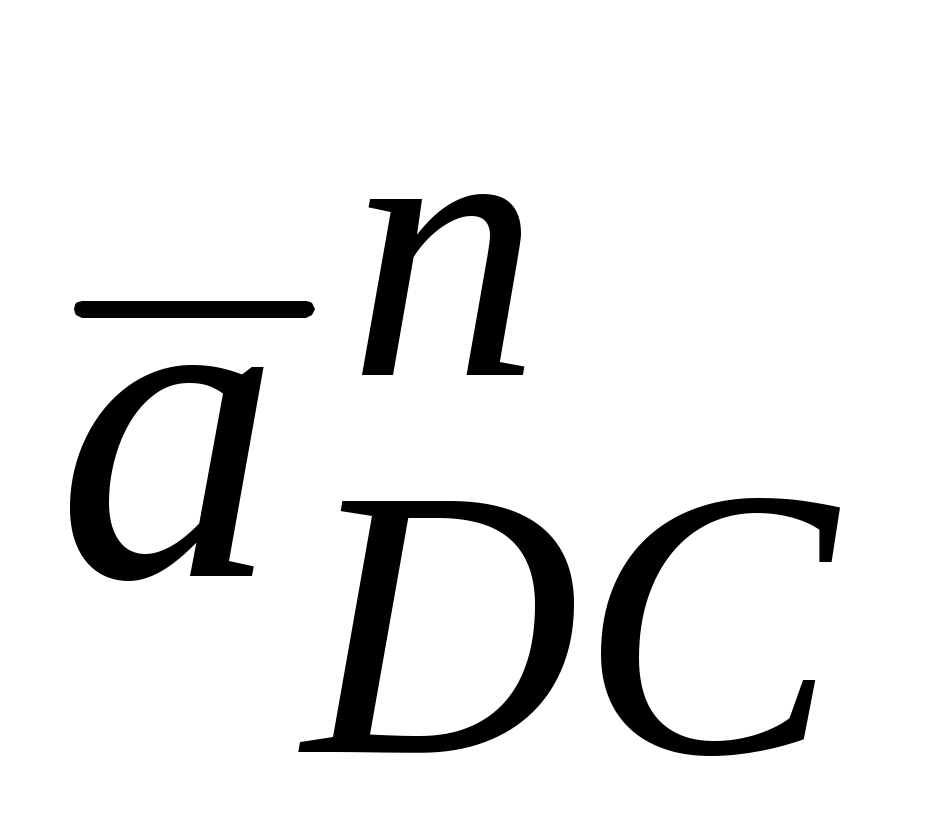 || DC. Конец вектора обозначим через n′ и через эту точку проводим направление
|| DC. Конец вектора обозначим через n′ и через эту точку проводим направление 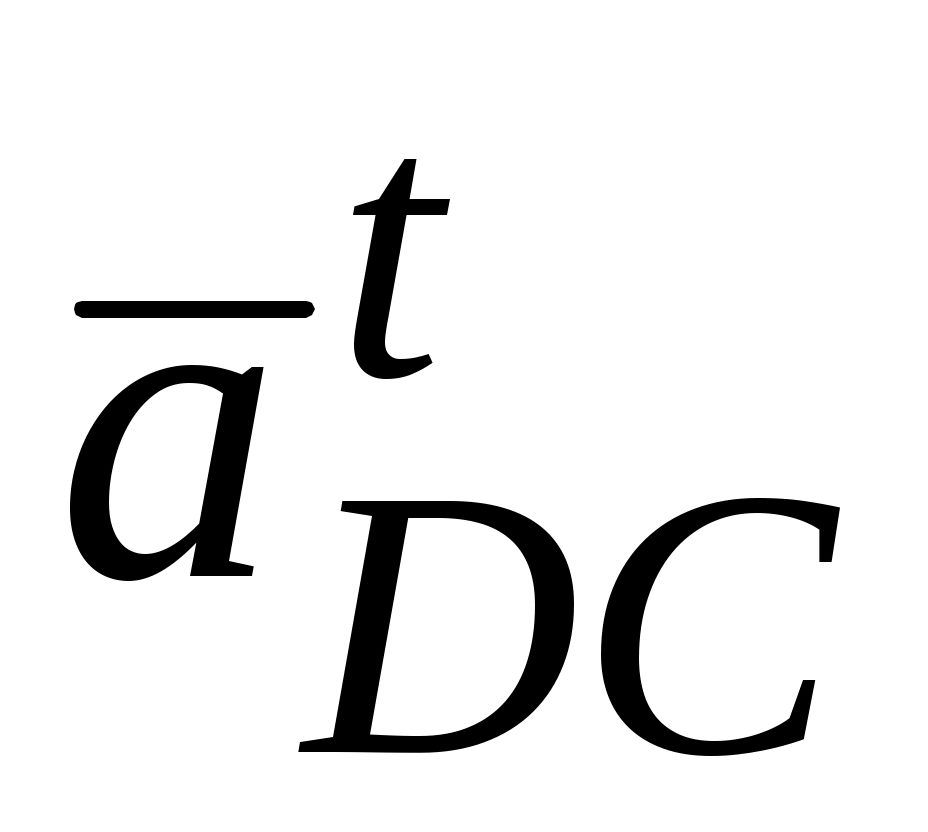
 DC до пересечения с направлением xx. Получаем точку
DC до пересечения с направлением xx. Получаем точку 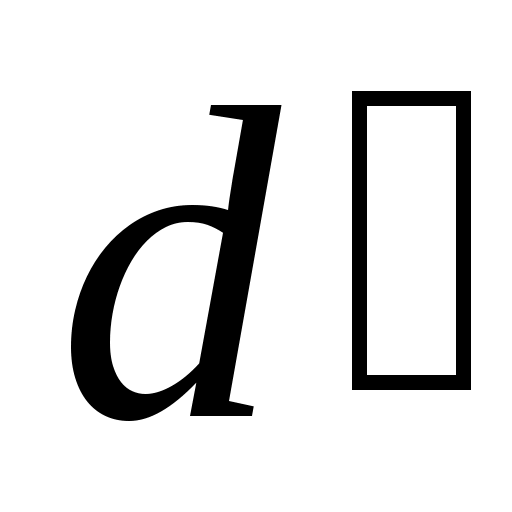 конец вектора
конец вектора 
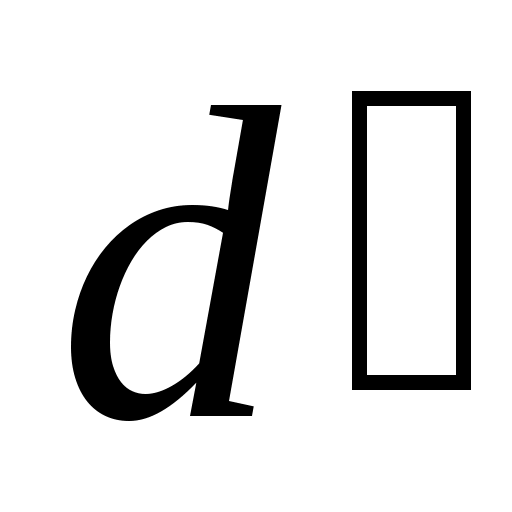
 Модуль вектора
Модуль вектора
׀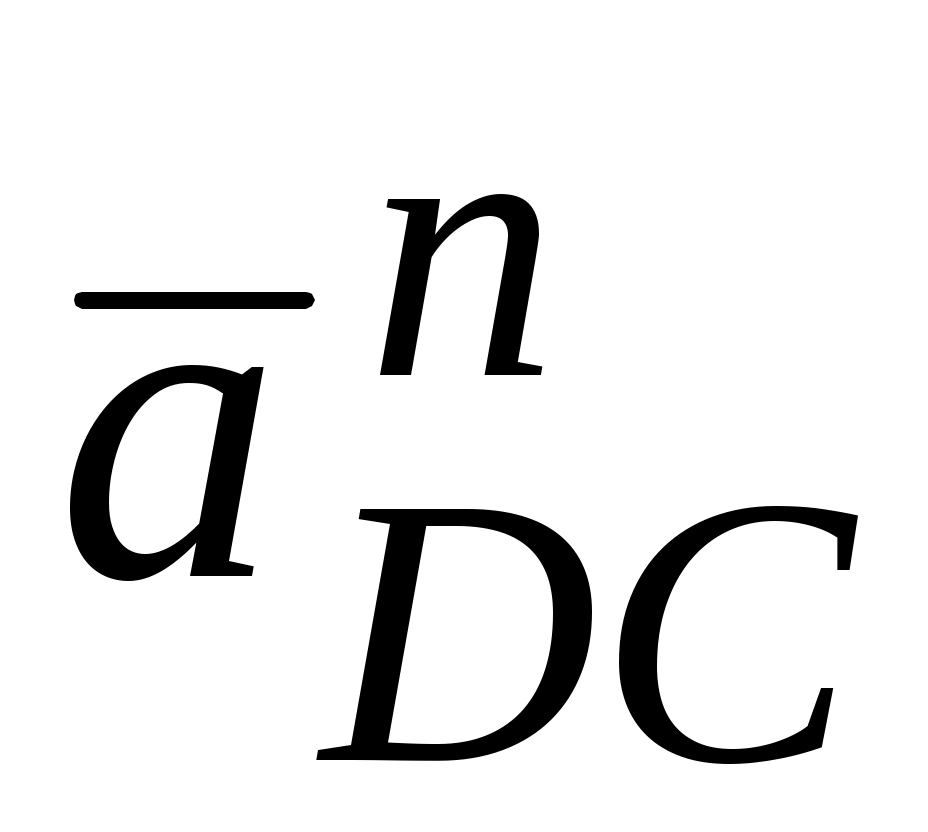 ׀ =
׀ = 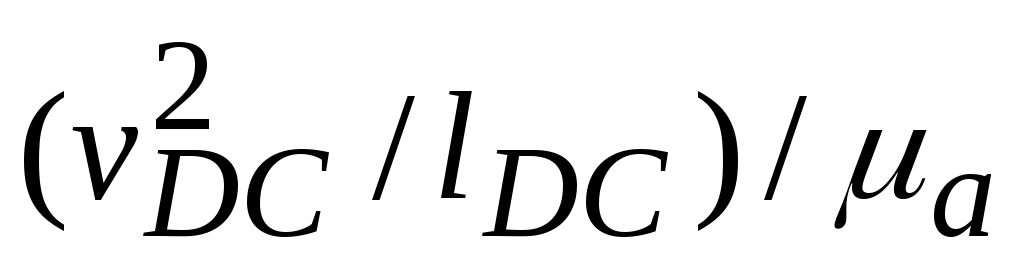 в мм.
в мм.

Рис.2.12. План ускорений механизма брикетировочного автомата
Рассмотрим построение плана ускорений для механизма компрессора (рис.2.10).
Начинаем с вычисления ускорения точки А, принадлежащей одновременно звеньям 1,2.
Для принятых исходных данных