Файл: Сборник тестов по математике саратов2016 Содержание Тесты входного контроля по дисциплине.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 994

Скачиваний: 24

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Ответы на тесты

Выберите два варианта ответов

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №2

1. Если функция f(x) является бесконечно большой величиной, то функция 1/f(x) является…

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №3 Отметьте верные утверждения односторонние пределы всегда меньше двустороннего сумма и разность бесконечно большой величины и ограниченной функции есть бесконечно большая величина если существует двусторонний предел, то существует и односторонние пределы равные ему же если функция монотонна и ограничена, то она не имеет предел Предел произведения функций равен… бесконечно малой величине произведению пределов этих функций бесконечно большой величине это ситуация неопределенности Впишите правильный ответ Пусть f: X R, a-предельная точка множества Х. Если функция имеет конечный предел при окрестности точки a.x a, то онав некоторой проколотой Выберите неверное утверждение: Дана функция f(x)  . x lim x0 lim x 0 lim x 0 lim f (x) не существуетf(x)  1f(x)  1f(x)  1 x  0 Отметьте примеры, в которых переход к эквивалентным совершен верно: x arcsin2 x x0x2 ; tgx sin x x0x x; C) (x 3)  sin(x 1) (x 3)(x 1) ;x0D) x2  tg(  x) x2 (  x) x Вычислить: limх3  8 12 ∞ 4 -4 x2 аrсtg(x 2) Пусть  (x) и (x)являются бесконечно малыми функциями при x a. Что можно сказать о функцияхx a (x)   (x); (x)   (x); (x) (x)при Бесконечно малая; бесконечно малая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; бесконечно малая Бесконечно малая; бесконечно большая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; стремится к 1 Пусть f положительная бесконечно большая, а gотрицательная бесконечно большая функции при x a. Что можно сказать о функциях f g;f g;f приgx a бесконечно малая; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; бесконечно малая бесконечно малая; отрицательная бесконечно большая; бесконечно малая Установить соответствие между 1 цифрой и 1 буквой а) формула, определяющая второй замечательный предел 1 f(x1), f(x2), f(x3),… f(xn), состоящая из значенийфункции, сходится к числу А. б) формула первого замечательного предела 2 lim (1 1)x ex x в) число А называется пределом функции f(x)в точке х=х0, если для любой,сходящейся к х0последовательности x1,x2,x3,…xn…, состоящей из значений аргумента, отличных от х0,соответствующая последовательность 3 lim sin x 1x0 x г) если функция имеет областьопределения на всей числовой оси, то ее предел в точке равен 4 значению функции в этой точке Число А называется пределом функции в точке Х0, когда к Х0 сходится последовательность из значений а) аргументаб) числовой осив) координатной плоскости г) функции 1   2   3   4   5   6   7   8   9   ...   14

Ответы на тесты

Тест №1

Тест №3

Ответы на тесты

Тест №1

Тест №2

Ответы на тесты


f g;

f g;

f(g(а)  0)

g

в точке aи.

( f g) ;

( f g)

_______;

( f)  (еслиg(а) 0)

g

  1. Найдите производную функции f(x) cos4 x:

A) f(x) 4sin xcos3 x

C) f(x) 4sin xcos x

B) f(x) 4sin xcos3 x

D) f(x) 4sin 3 xcos x

  1. Чему равна производная функции f(x) (5 x2 )10 :

A) f(x) 20x5 x2 9 B) f(x) 2x5 x2 9

C) f(x) 105 x2 9 D) f(x) 10x5 x2 9

  1. Найдите производную функции f(x) xarctg2x:

  1. f(x) arctg 2x

x


1 4x2

  1. f(x)

x


1 x2

  1. f(x) arctg 2x

2x


1 x2

  1. f(x)

2x

1 4x2

  • arctg 2x

  1. Чему равна производная функции


9x 2x 3

2  

f(x)


f(x)

x2 3x:

x2 1

3x2 2x 3




A) (x2 1)2

  1. f

(x)

(x2 1)2

  1. f

(x)

3x2 2x 3


(x2 1)2

  1. f

(x)

3x2 2x 3


x2 1
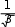
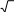Тест №2




  1. Найти производную функции

y(x)

arctg

3x. 1 x2

А) 1 х2

1 х2 х4

С) 1

(1 х2 )2

В) 3

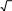(1 х2 )2

D) 1 х2

1 х2 х4

  1. Найти дифференциал функции

(x)

1


ln х

в точке x=e

A) (1/e)dx B) e

  1. e de D) e+dx

  1. Вычислить, используя правило Лопиталя: а) lim

x0
ln( x1) xtg2 x

A) 0 B) -1/2

C) -1 D) ∞

  1. Вычислить, используя правило Лопиталя:

A) -1 B) 0

C) ∞ D) -2


lim


x0
(1 e2x)ctgx

  1. Вычислить вторую производную функции точке х=0

    1. 2 B) 4

C) 0 D) -1/2

f(x) e x2 (x4 2x2 2) в

  1. Вставьте пропущенные фразы в теореме Лагранжа: пусть fнепрерывна

на [a;b]

и дифференцируема на. Тогдаc(a;b) :

f(b)

f(a)

.

  1. Установите соответствие




1) Функция f называется

монотонно возрастающей на множестве Х, если
1) f(х) 0, х Х

2) Для того чтобы дифференцируемая функция f

монотонно возрастала на множестве Х необходимо и

достаточно, чтобы
2) f(х) 0, х Х

3) Для того чтобы дифференцируемая функция f

монотонно убывала на
3) х1, х2 Х: х1 х2 f(х1) f(х2 )

множестве Х необходимо и

достаточно, чтобы



4) Функция fназывается монотонно убывающей на множестве Х, если
4)х1, х2 Х: х1 х2 f(х1) f(х2 )

  1. Пусть

f: X R,

a X. Точка aназывается точкой локального

максимума функции f, если

А) lim

xa

f(x)

f(a)

В) Ua: f(a)

f(x),

xUa∩ X

С) f(a) 0

  1. fменяет знак при переходе через точку aслева на право с плюса на минус

  1. Установите соответствие:




1) Понятие точки перегиба графика функции
1) Если a-точка перегиба графика

функции fи функция дважды

дифференцируема в этой точке, то

f (a) 0 .

2) Необходимое условие точки перегиба
2) Пусть f: X R, a X. Точка

a называется точкой перегиба графика функции f , если при переходе через точку (а,(а)) график меняет

направление выпуклости.

3) Достаточное условие точки перегиба
3) Пусть a-точка подозрительная на

перегиб функции f, функция дважды

дифференцируема в некоторой проколотой окрестности точки a . Если при переходе через точку a, f

меняет знак, то эта точка является точкой перегиба графика функции f.

  1. Пусть fдважды дифференцируема на множестве Х. Для того, чтобы

график функции f был направлен выпуклостью вверх на множестве Х, необходимо и достаточно, чтобы

А) х1, х2 Х:

х1 х2

f(х1)

f(х2 )

В) f(х) 0,

С) f (х) 0,

D) f (х) 0,

хХ

х Х

х Х

Смотрите также файлы