ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 180
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
РГУ нефти и газа (НИУ) имени И.М. Губкина
| Факультет | Автоматики и вычислительной техники |
| Кафедра | Автоматизации технологических процессов |
| Оценка комиссии: | | Рейтинг: | | ||
| Подписи членов комиссии: | |||||
| | | | |||
| (подпись) | | (фамилия и.о.) | |||
| | | | |||
| (подпись) | | (фамилия и.о.) | |||
| | |||||
| (дата) | |||||
| | | | |||
КУРСОВАЯ РАБОТА
| по дисциплине | Теория автоматического управления |
| на тему | Расчёт системы автоматического управления объекта |
| регулирования концентрации заданного компонента в смесителе | |
| | |
| «К ЗАЩИТЕ» | | ВЫПОЛНИЛ: | |
| | | Студент группы | АТ-19-01 |
| | | | (номер группы) |
| Ст. преподаватель; Мартынова А.Ю. | | Беляева Мария Михайловна | |
| (должность, ученая степень; фамилия, и.о.) | | (фамилия, имя, отчество) | |
| | |  | |
| (подпись) | | (подпись) | |
| | | 31.05.2022 | |
| (дата) | | (дата) | |
| Москва, 20 | 21 | |

Оглавление
1. РАСЧЕТ ЛИНЕЙНОЙ ЧАСТИ 6
1.1 Составление передаточной функции объекта управления. 6
1.2. Составление передаточной функции клапана. 10
1.3 Составление замкнутой структуры с двумя входами 12
1.4 Вывод передаточных функций по заданию и возмущению 14
1.7 Синтез последовательного корректирующего устройства метода ЛАХ 24
1.8 Построение амплитудно-частотной характеристики скорректированной замкнутой системы и определение показателя колебательности M. 27
1.9 Аналитическое конструирование регулятора 28
2. РАСЧЁТ НЕЛИНЕЙНОЙ СИСТЕМЫ 35
2.1 Построение фазового портрета методом припасовывания с применением метода изоклин 35
2.2. Исследование скользящего режима и условий скачков 47
2.3 Расчёт автоколебаний (АК) методом гармонического баланса 54
54
2.4 Исследование условий абсолютной устойчивости: сравнение результатов 64
3. РАСЧЕТ ДИСКРЕТНОЙ СИСТЕМЫ 73
3.1. Расчет передаточной функции разомкнутой импульсной системы (РИС) 73
3.2. Передаточная функция разомкнутой импульсной системы с типовым цифровым регулятором 78
3.3. Вывод передаточных функций замкнутой импульсной системы (ЗИС) с типовыми цифровыми регуляторами 82
3.4. Исследование устойчивости и вычисление критического коэффициента усиления с использованием алгебраического и частотного критериев устойчивости. 84
3.5. Исследование показателей качества ЗИС с типовыми регуляторами (Определение быстродействия ЗИС). 91
3.6. Определение статической ошибки ЗИС с типовыми регуляторами 93
3.7 Построение переходного процесса по каналу задания в ЗИС с регулятором методом степенных рядов. 97
3.8. Синтез импульсного регулятора, обеспечивающего переходный процесс конечной длительности 100
Литература 107
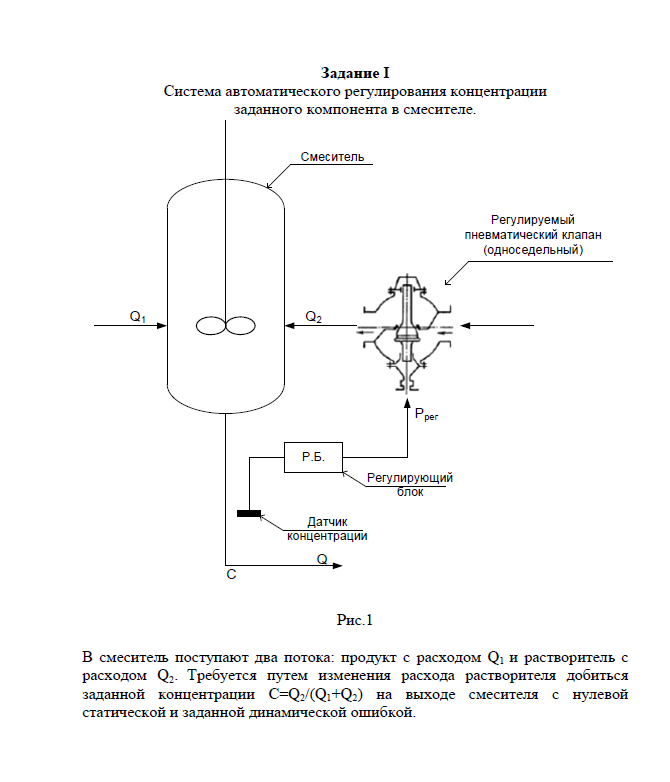

1. РАСЧЕТ ЛИНЕЙНОЙ ЧАСТИ
1.1 Составление передаточной функции объекта управления.


Рисунок 1.1 –
Структурная схема замкнутой системы
где f(t) – сигнал входа возмущения;
u(t) – сигнал управления, поступающий после прохождения клапана;
e(t) – сигнал статической ошибки;
g(t) – сигнал входа задания;
x(t) – сигнал выхода.

 Выведем дифференциальное уравнение объекта регулирования концентрации в смесителе.
Выведем дифференциальное уравнение объекта регулирования концентрации в смесителе.

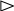 Q2
Q2  Q1
Q1

Q= Q1 + Q2
Рисунок 1.2 – Схема объекта регулирования концентрации в смесителе
где Q1 – продукт расхода на входе смесителя;
Q2 – растворитель с расходом на входе смесителя;
Q – расход количества жидкости на выходе из смесителя;
μ – степень открытия клапана.
Необходимо добиться заданной концентрации на выходе:
С=
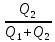 (1.1.1)
(1.1.1)F=
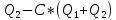 (1.1.2)
(1.1.2)В положении равновесия:
F*=
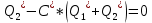 (1.1.3)
(1.1.3)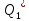 – номинальный расход;
– номинальный расход;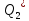 – номинальный растворитель с расходом;
– номинальный растворитель с расходом;C* – значение концентрации смеси на выходе смесителя;
Материальный баланс по Q2 – номинальный режим.
Запишем дифференциальное уравнение при нарушении положения равновесия:
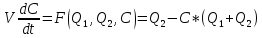 (1.1.4)
(1.1.4)Линеаризуем уравнение в окрестности номинальной точки:
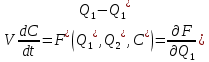 )+
)+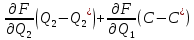 (1.1.5)
(1.1.5)Запишем дифференциальное уравнение, разложив в ряд Тейлора концентрацию смеси на выходе:
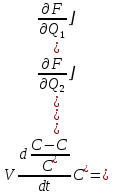
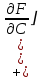 (1.1.6)
(1.1.6) Введем обозначения:
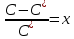
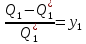
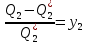 (1.1.7)
(1.1.7)Учитывая (1.1.3):
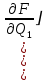
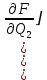 =1-
=1-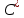
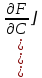 (1.1.8)
(1.1.8)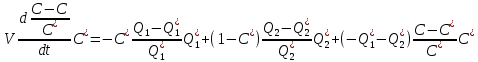 (1.1.9)
(1.1.9)Подставляя (1.1.7) в уравнение (1.1.9), получаем:
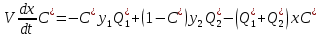
Поделим уравнение на коэффициент при x:
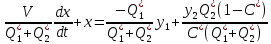 (1.1.11)
(1.1.11)Введем обозначения:
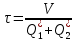
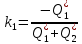
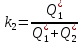 (1.1.12)
(1.1.12)где k1 и k2 – безразмерные коэффициенты;
τ – постоянная времени объекта:
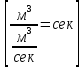 .
.Произведем необходимые расчеты:
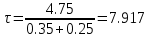 (1.1.13)
(1.1.13)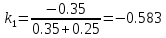 (1.1.14)
(1.1.14)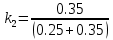 =0.583 (1.1.15)
=0.583 (1.1.15)Запишем итоговое уравнение:
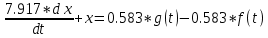 (1.1.16)
(1.1.16)Передаточная функция объекта регулирования выглядит следующим образом:
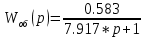 (1.1.17)
(1.1.17)1.2. Составление передаточной функции клапана.