Файл: Автоматики и вычислительной техники.docx

3.8. Синтез импульсного регулятора, обеспечивающего переходный процесс конечной длительности

Быстродействие импульсной системы определяется максимально приближенным к единице модулем корня характеристического многочлена. Чем меньше максимальный модуль, тем больше степень устойчивости системы. Наконец, если модули всех корней равны нулю, система обладает бесконечно – большой степенью устойчивости. При этом введенное ранее понятие «количество импульсов, за которое переходный процесс входит в 5%-трубку точности» лишается смысла, т.к. такое количество равно нулю. Однако, переходный процесс достигает своего установившегося значения за конечное число импульсов, равное порядку системы.

1. 
   По каналу задания
   

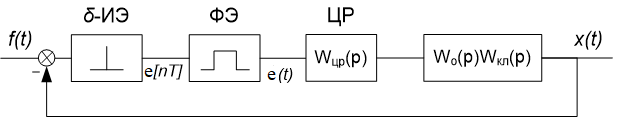
Рисунок 3.13– Структурная схема рассматриваемой системы

Приведенная передаточная функция РИС имеет следующий вид:

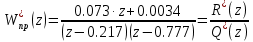Передаточная функция цифрового регулятора, обеспечивающего бесконечно большую степень устойчивости:

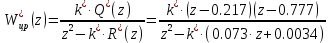Передаточная функция РИС с цифровым регулятором:

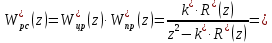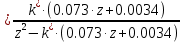Передаточная функция ЗИС с бесконечно большой степенью устойчивости:

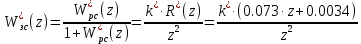Выберем

---

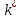
регулятора конечной длительности так, чтобы ЗС получилась астатической (т.е чтобы ее статическая ошибка была нулевой):

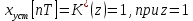Определим коэффициент :

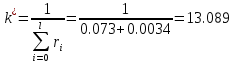Передаточная функция ЗИС с бесконечно большой степенью устойчивости:

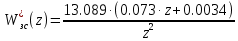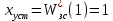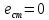Рассмотрим реакцию системы на единичный скачок



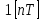
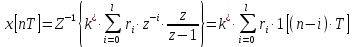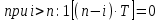
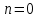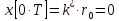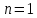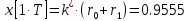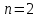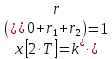Построим график переходного процесса по заданию:



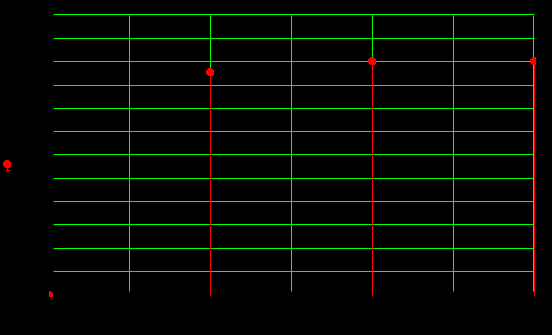
Рисунок 3.14 – Переходный процесс конечной длительности ЗИС по заданию

---

Проверяем результат с помощью теоремы о конечных значениях:

2. 
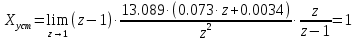   По каналу возмущения
   

Рассмотрим следующую структурную схему:



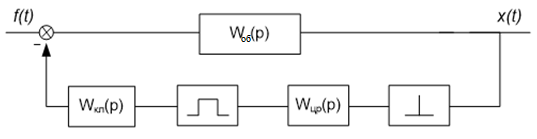
Рисунок 3.15 – Структурная схема системы по каналу возмущения

Преобразуем эту систему к виду:



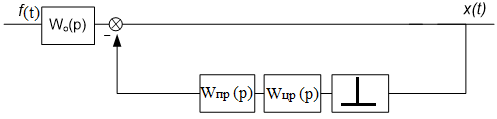
Рисунок 3.16 – Преобразованная снова структурная схема системы по каналу возмущения

Передаточная функция обратной связи совпадает с передаточной функцией разомкнутой системы по каналу задания.

Напишем изображение выходной величины:

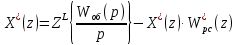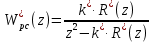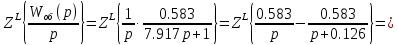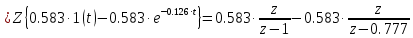Величина на выходе системы по каналу возмущения:

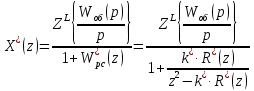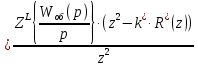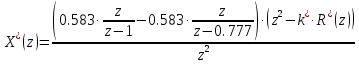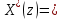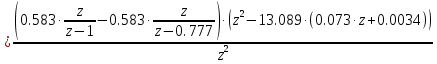Преобразуем в пакете Mathcad:

---

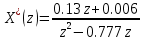По теореме о конечных значениях установившееся значение выходного сигнала в системе:

,

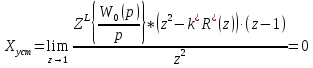что очевидно, поскольку коэффициент усиления регулятора подбирается исходя из условия

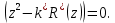
Для построения переходного процесса разложим изображение выходной величины на простые дроби и возьмем обратное Z-преобразование:

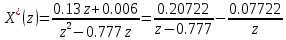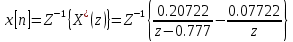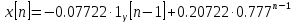Построим график переходного процесса по возмущению:



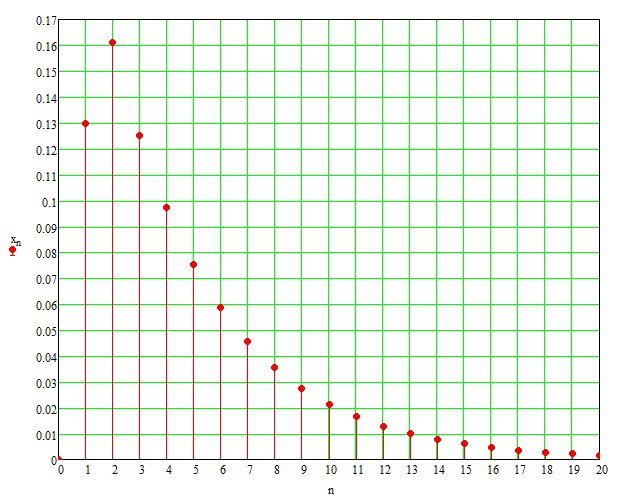
Рисунок 3.17 – Переходный процесс конечной длительности ЗИС по возмущению

Литература

1. 
   Гершкович Ю.Б., Полякова О.А. Методические указания к курсовой работе по дисциплине «Теория автоматического управления». Часть 1. Расчет линейной системы автоматического регулирования с ПИ-регулятором. М.: РГУ нефти и газа (НИУ) имени И.М. Губкина, 2008 – 42 с.
   
2. 
   Ким Д.П. Теория автоматического управления. Т.1. Линейные системы. – М.: Физматлит, 2003. – 288 с.
   
3. 
   Гершкович Ю.Б. Методические указания к курсовой работе по дисциплине «Теория автоматического управления». Часть 2. Расчет нелинейной системы автоматического регулирования с типовыми статическими нелинейностями; Часть 3. Расчет дискретной системы автоматического регулирования с типовыми цифровыми регуляторами. М.: РГУ нефти и газа (НИУ) имени И.М. Губкина, 2009 – 62 с.
   
4. 
   Ким Д.П. Теория автоматического управления. Т.2. Многомерные, нелинейные, оптимальные и адаптивные системы: Учеб. Пособие. – М.: Физматлит, 2004. – 464 с.
   

---

---