Файл: Автоматики и вычислительной техники.docx

Статическая характеристика клапана (Q₂ = f(P_рег))

Табл.1.2.1

Ррег (атм)	0	0.15	0.25	0.35	0.5	0.6	0.7	0.8	1.0
Q2 (м3/сек)	0	0	0.02	0.09	0.3	0.65	0.75	0.8	0.8

Динамическая характеристика клапана (Q₂ = f(t))

Табл.1.2.2

t (сек)	0	0.7	1.2	1.8	2.5	3.0	3.5	∞
Q2 (м3/сек)	0.1	0.3	0.4	0.46	0.5	0.56	0.58	0.6

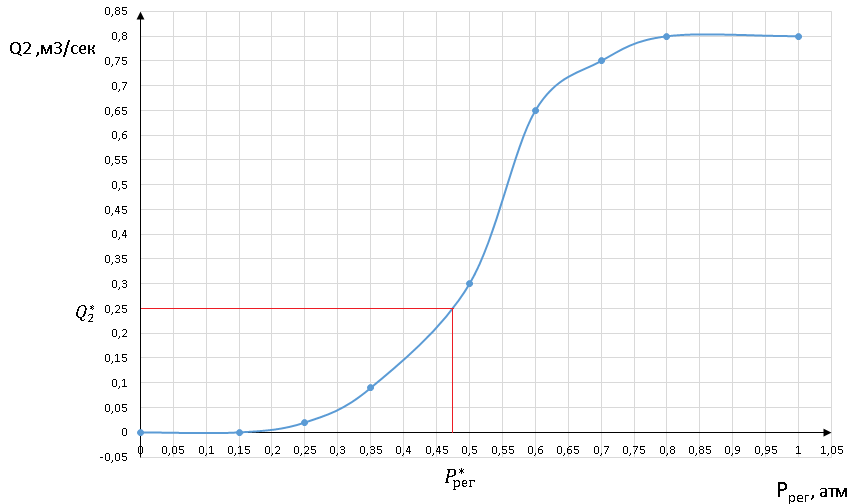
Рисунок 1.3 – Статическая характеристика клапана

Согласно графику, номинальному значению Q₂ соответствует номинальное значение давления равное 0.462 атм.

Определим коэффициент усиления клапана:





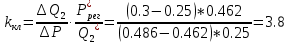
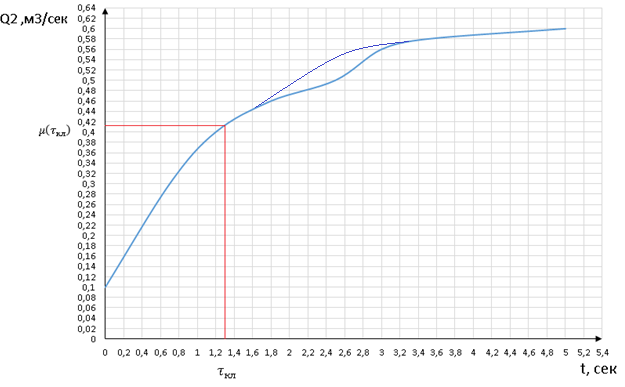
Рисунок 1.4 – Динамическая характеристика клапана

Динамическую характеристику клапана можно описать экспоненциальной функцией:

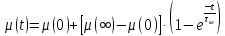Определим постоянную времени клапана. При t = τ_кл функция степени открытия клапана равна μ(τ_кл):



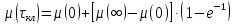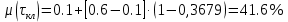По графику определяем постоянную времени клапана t

---

_кл: t_кл=1.31 сек

Полученная функция:



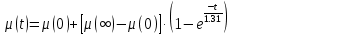
Убедимся, что найденная функция верная, подставив значения времени и сравнив их со значением расхода Q₂ из таблицы 1.2.2:

Рассчитанное	0.1	0.306	0.399	0.473	0.525	0.549	0.565	0.599
По условию	0.1	0.3	0.4	0.46	0.5	0.56	0.58	0.6

Значения практически равны, следовательно, постоянная времени t_кл найдена верно.

Передаточная функция клапана выглядит следующим образом:


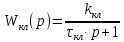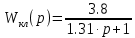1.3 Составление замкнутой структуры с двумя входами

Передаточная функция регулятора имеет вид:

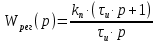где k_п – коэффициент усиления пропорционального регулятора (П-регулятора);

τ_и – постоянная времени интегрирующего звена (И-регулятора).



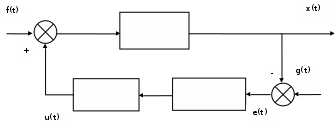
Рисунок 1.5 – Структурная схема замкнутой системы

Прямое преобразование Лапласа сигнала выхода имеет вид:



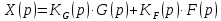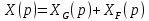1.4 Вывод передаточных функций по заданию и возмущению

Передаточная функция замкнутой системы по заданию:

---

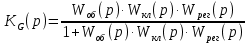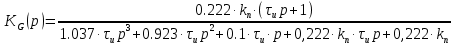Передаточная функция замкнутой системы по возмущению:



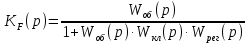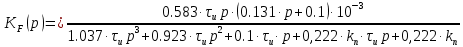1.5 Исследование статики замкнутой системы

Идеальная система должна иметь 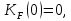а 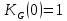. Тогда система не будет реагировать на возмущение и будет в точности отслеживать сигнал задания.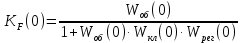







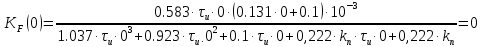
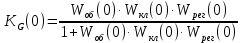
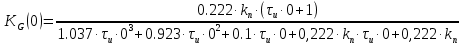=1

Требования статики выполнены:





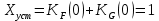
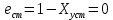
Вывод: система астатическая.

1.6 Расчет динамики
Настройка изодромного регулятора по критерию максимальной степени устойчивости, построение двух корневых годографов (по коэффициенту усиления и постоянной времени регулятора), определение быстродействия и показателя колебательности, сравнение косвенных и прямых показателей качества (непосредственно по графику переходного процесса).

Схема по входу задания



Рисунок 1.6 – Структурная схема по входу задания



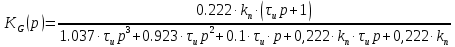
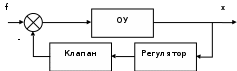Схема по входу возмущения

Рисунок 1.7 – Структурная схема по входу возмущения



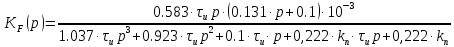
Характеристический многочлен:



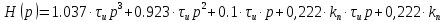
Чтобы наша система 3-го порядка имела максимальную возможную степень устойчивости, необходимо, чтобы все корни лежали на одном расстоянии от мнимой оси.

Необходимый критерий устойчивости выполнен (все коэффициенты положительные).

---

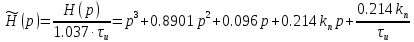
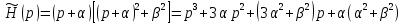
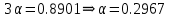
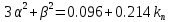
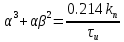
Пусть β = 0.5;

Тогда k_п = 1.954; τ_и = 4.169 с

Тогда корни характеристического уравнения равны:



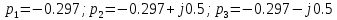
Время регулирования:



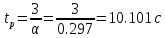
Построим корневые годографы, чтобы проанализировать движение корней характеристического уравнения замкнутой системы, которое влияет на изменение свойств системы при изменении настроечных параметров.

1. 
   По коэффициенту усиления k_п (при ранее найденном τ_и = 4.169 с)
   

Запишем передаточную функцию разомкнутой системы:





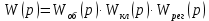
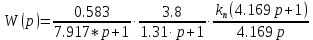
Полюса:

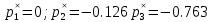
Нули:

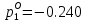
n = 3; m = 1; n–m = 2

Найдём центр звезды асимптот





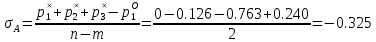
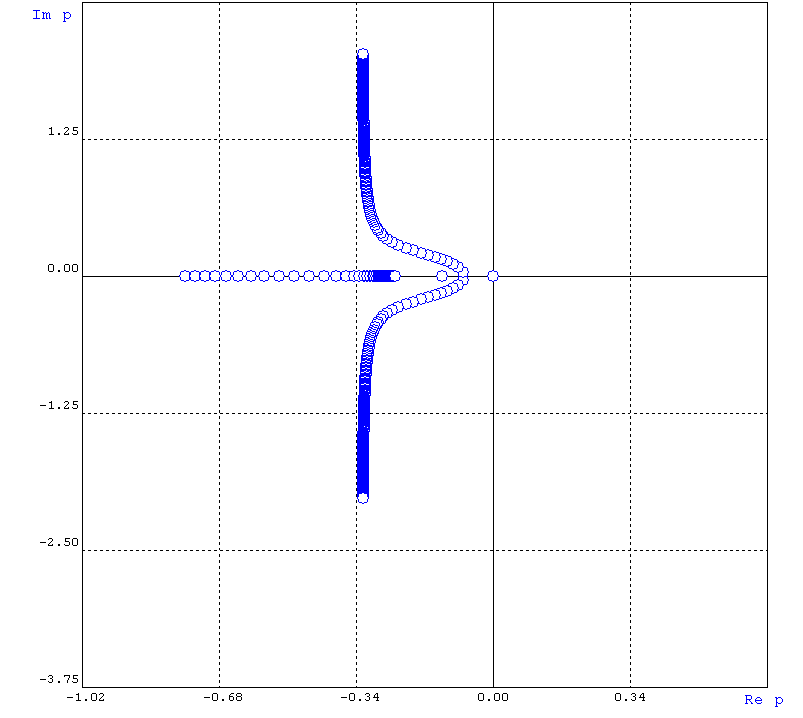
Рисунок 1.8 – Годограф по коэффициенту усиления

По критерию Раута-Гурвица:









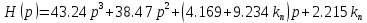
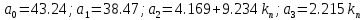
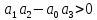
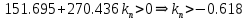
Коэффициент усиления не может быть отрицательным, поэтому k_п > 0. Система устойчива при .

2. 
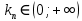   По постоянной времени τ_и (к примеру, k_п = 1.954)
   

Запишем передаточную функцию разомкнутой системы:

---

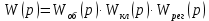
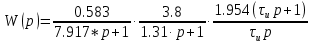
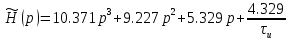
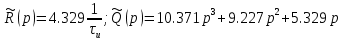
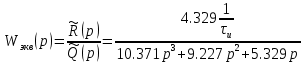
Построим корневой годограф по 1/ τ_и

Полюса:

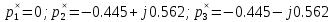
n = 3; m = 0; n–m = 3

Найдём центр звезды асимптот





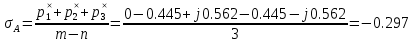
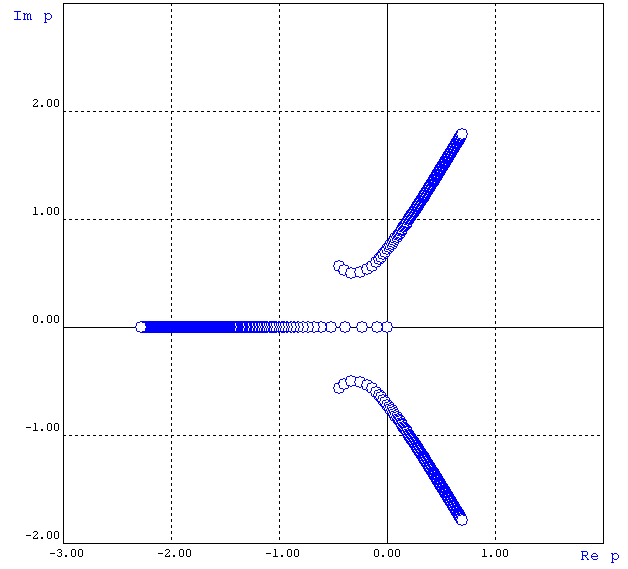
Рисунок 1.9 – Корневой годограф по 1/ τ_и

По критерию Раута-Гурвица:









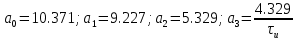
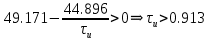
Система устойчива при τ_и > 0.913, т.е. для рассчитанного ранее τ_и=4.169 система является устойчивой, .

Построение переходного процесса нескорректированной системы по входам задания и возмущения и сравнение прямого и косвенного времени регулирования.







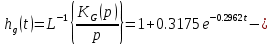
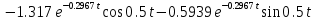
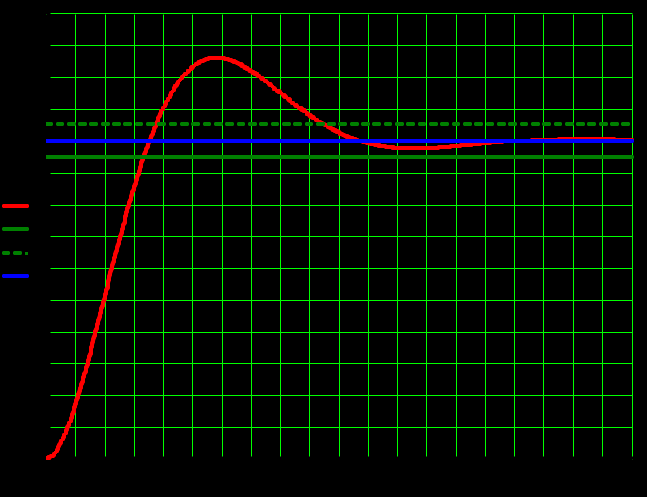
Рисунок 1.10 – Переходный процесс нескорректированной системы по входу задания

Время регулирования: по графику: t_{р прямое} = 9.53 с

вычисленное: t_{р косвенное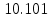} = с.

Колебательность процесса:

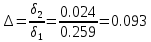
Степень колебательности:

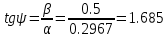
Перерегулирование:






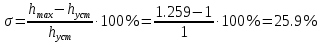
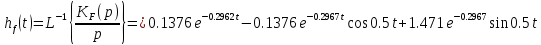
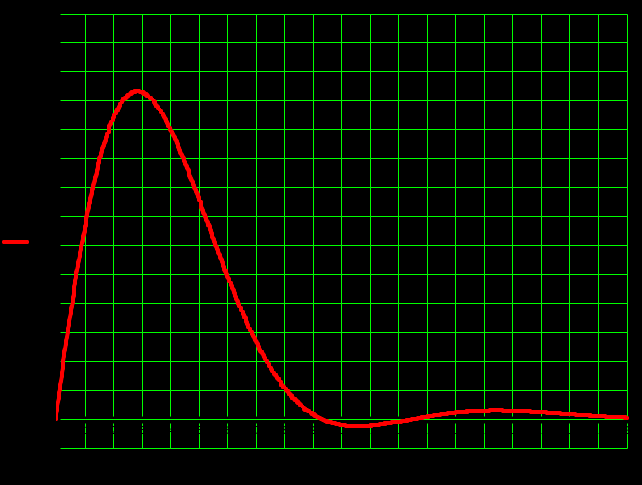
Рисунок 1.11 – Переходный процесс нескорректированной системы по входу возмущения

Переходный процесс по возмущению выходит из 5-% трубки точности.

Построение амплитудно-частотной характеристики системы и определение показателя колебательности М.

---