Файл: Автоматики и вычислительной техники.docx

I. Частотный критерий абсолютной устойчивости (критерий Попова)


Рисунок 2.22 – Структурная схема замкнутой системы для исследования абсолютной устойчивости по критерию Попова



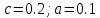
Асимптотически устойчивая нелинейная система является абсолютно устойчивой в заданном классе нелинейных статических характеристик, если она асимптотически устойчива для любой характеристики из этого класса.

Критерий Попова:

Нелинейная система абсолютно устойчива в классе нелинейности k_m, если существует число 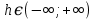, при котором выполняется условие: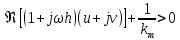





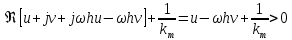
Модифицированная АФХ:

1. 
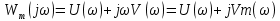
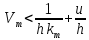
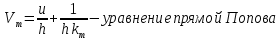
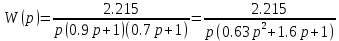
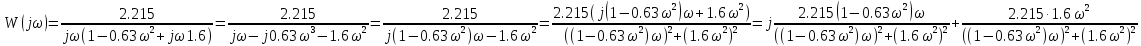
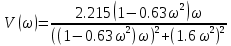
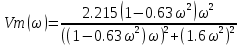
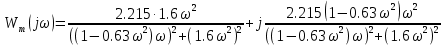
   Идеальное реле
   

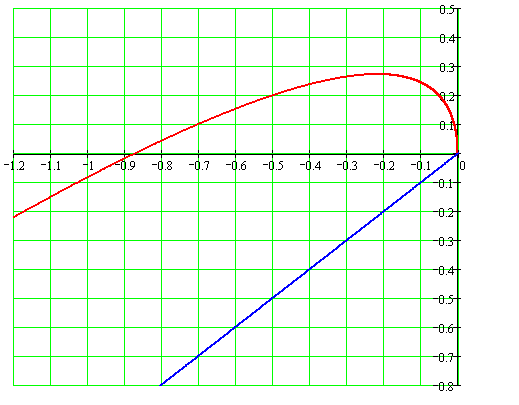
Рисунок 2.23 – График модифицированной АФХ непрерывной линейной части и линии Попова для идеального реле

Нелинейный элемент – идеальное реле. Для него 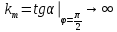,. Это означает, что точка 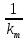– начало координат.

При любом значении h частотный критерий Попова для идеального реле не выполняется, поскольку модифицированная АФХ непрерывной линейной части никогда не будет ниже линии Попова. Это означает, что всегда возможны автоколебания. (При исследовании системы по методу гармонического баланса получили такой же результат – в системе всегда будут автоколебания).

2) Реле с зоной нечувствительности

Выразим k_гр, приравняв действительные части модифицированной АФХ и линии Попова:

---

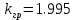
Рассмотрим 3 случая:

а)











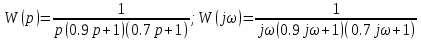
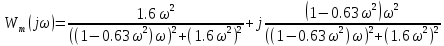
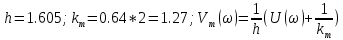
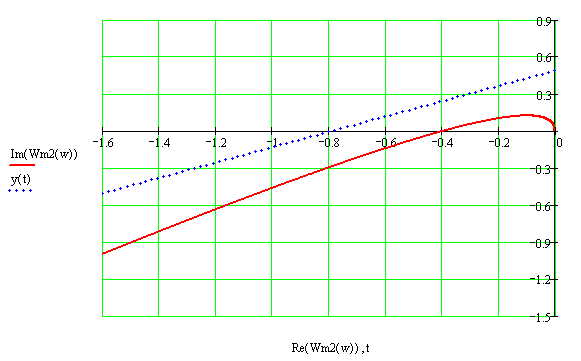
Рисунок 2.24 – График модифицированной АФХ непрерывной линейной части и линии Попова для зоны нечувствительности с коэффициентом усиления k = 1

При значении h=1 (kgr) частотный критерий Попова для реле с зоной нечувствительности выполняется, поскольку модифицированная АФХ непрерывной линейной части целиком лежит ниже линии Попова. Нет автоколебаний, асимптотическая устойчивость.

б)

Аналогичным образом поступаем, как и в предыдущем пункте и получаем:





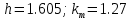
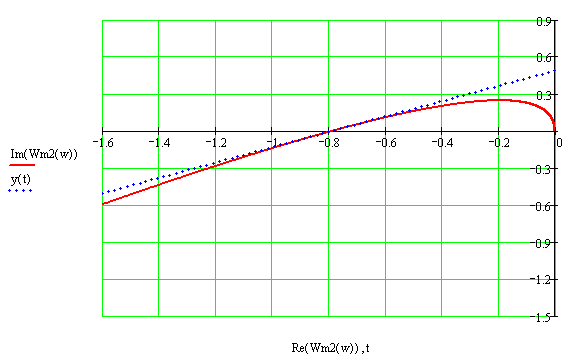
Рисунок 2.25 – График модифицированной АФХ непрерывной линейной части и линии Попова для зоны нечувствительности с коэффициентом усиления k = k_гр = 1.995

При значении h=1.605 (k=k_gr) модифицированная АФХ непрерывной линейной части касается линии Попова - граничный случай.

в)

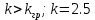
Аналогичным образом поступаем, как и в предыдущих двух пунктах и получаем:





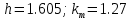
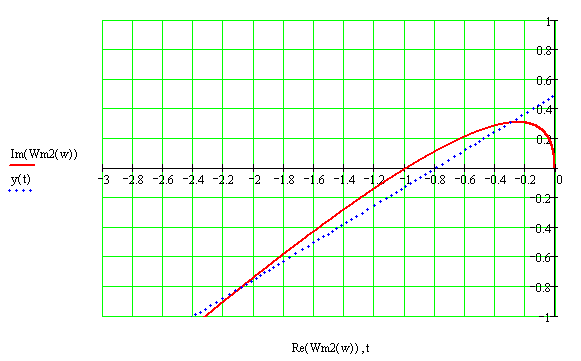
Рисунок 2.26 – График модифицированной АФХ непрерывной линейной части и линии Попова для зоны нечувствительности с коэффициентом усиления k = 2.5

При любом значении h (k>k_gr) частотный критерий Попова для реле с зоной нечувствительности не выполняется, поскольку модифицированная АФХ непрерывной линейной части целиком никогда не будет ниже линии Попова. Система неустойчива, существуют автоколебания.

II. Введем местную обратную связь:


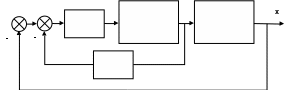
Рисунок 2.27 – Структурная схема замкнутой системы для стабилизации автоколебаний







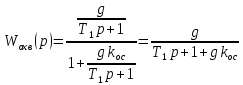
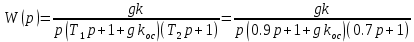
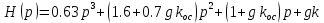
По критерию Раута-Гурвица:









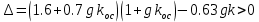
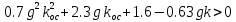
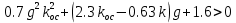
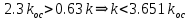
Пусть k_ос = 1, k = 3 (из области устойчивости), тогда:





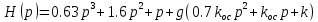
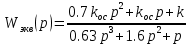
Эквивалентная передаточная функция:





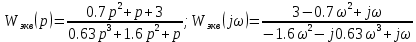
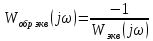
Проверим частотный критерий Попова для стабилизированной системы (для системы с местной обратной связью).









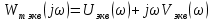
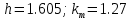
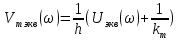
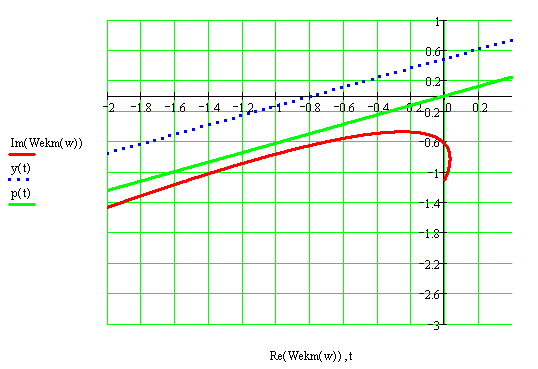
Рисунок 2.28 – График модифицированной АФХ эквивалентной передаточной функции стабилизированной системы (системы с местной обратной связью)

При значении h=1.605 частотный критерий Попова для стабилизированной системы выполняется, поскольку модифицированная АФХ непрерывной линейной части целиком лежит ниже линии Попова.

Метод гармонического баланса:







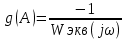
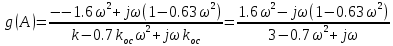
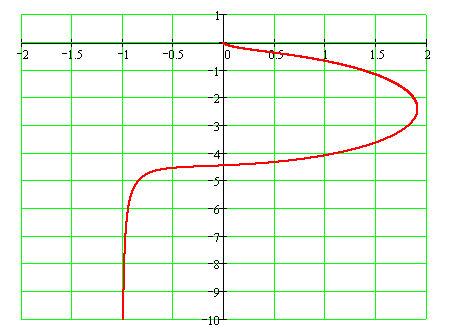
Рисунок 2.29 – График инверсной эквивалентной АФХ

Уравнение гармонического баланса не имеет решения. График J(A) расположен на положительной действительной полуоси. Автоколебания невозможны, система асимптотически устойчива

3. РАСЧЕТ ДИСКРЕТНОЙ СИСТЕМЫ

3.1. Расчет передаточной функции разомкнутой импульсной системы (РИС)

Разомкнутая дискретная (импульсная) система без регулятора представлена на рисунке ниже.



Рисунок 3.1 – Структурная схема системы

Входной сигнал 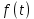подается на реальный импульсный элемент (РИЭ), выходом которого является сигнал 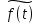– последовательность прямоугольных импульсов, модулированных по амплитуде. Математическая модель РИЭ распадается на два последовательных гипотетических элемента: 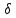– импульсный элемент, формирующий последовательность 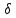– импульсов, представляющих математическую абстракцию, и формирующий элемент (ФЭ), формирующий последовательность вполне реальных прямоугольных импульсов, модулированных по амплитуде. Сигнал 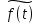является входом непрерывной линейной части, состоящей из объекта и исполнительного механизма, реакция которой на этот вход представляет собой выход системы.

Передаточная функция формирующего элемента, здесь 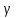- скважность импульсов, Т – период квантования.



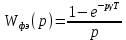Выберем скважность 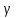и период квантования .



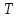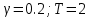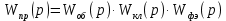– приведенная передаточная функция непрерывной линейной части, представляющей собой последовательное соединение объекта, клапана и формирующего элемента.



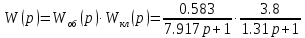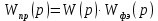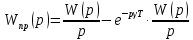Обозначим:



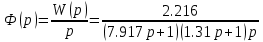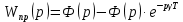Разложим 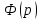на простые дроби:



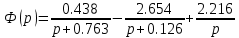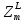– преобразование от этой функции выглядит следующим образом:



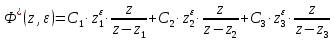В этом выражении:



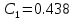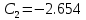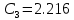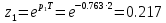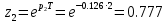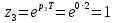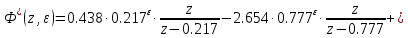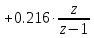Тогда передаточная функция разомкнутой импульсной системы без регулятора находится как 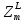-преобразование передаточной функции приведенной непрерывной линейной части:



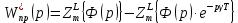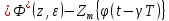Обозначим:



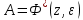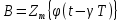Слагаемое было найдено ранее: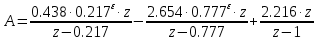



Рассмотрим слагаемое , которое находится по теореме запаздывания: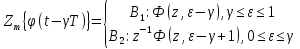



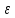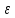Поэтому передаточная функция разомкнутой импульсной системы состоит из двух формул: «верхней» и «нижней» в зависимости от выбранного параметра , 0 ≤ ≤ 1.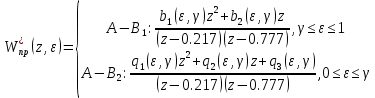



Здесь коэффициенты зависят от заданной скважности 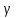и выбранного параметра :



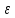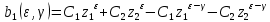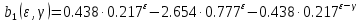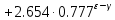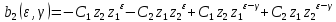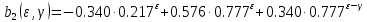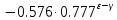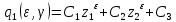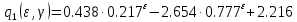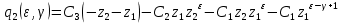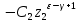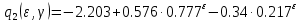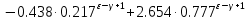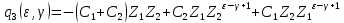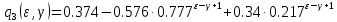Проверка: при 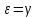«верхняя» и «нижняя» формулы сходятся:



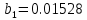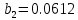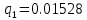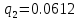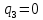Для дальнейших расчетов особый интерес представляет случай 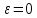, соответствующий моментам времени, кратным периоду квантования. Коэффициенты передаточной функции в этом случае вычисляются по «нижней» формуле. Для 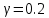имеем:



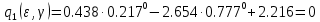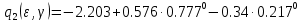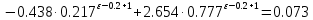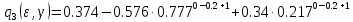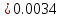Таким образом разомкнутая передаточная функция импульсной системы пр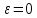и и 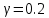будет равна:




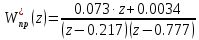3.2. Передаточная функция разомкнутой импульсной системы с типовым цифровым регулятором

П-регулятор (пропорциональный регулятор).


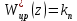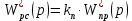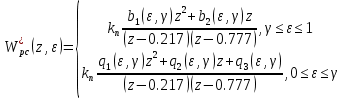При



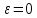
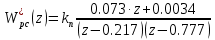Построим АФХ данной разомкнутой дискретной системы. Положим 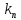=1, .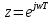



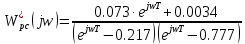w=п/2

w=0


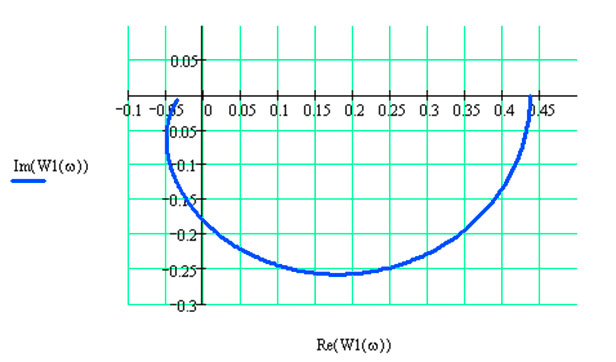
Рисунок 3.2 – АФХ разомкнутой импульсной системы с П-регулятором.
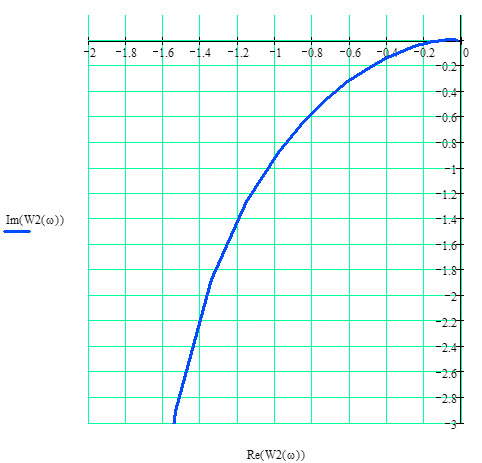
И-регулятор (интегральный регулятор).


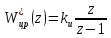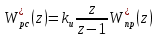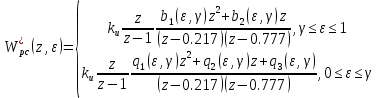При



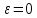
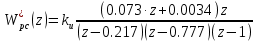Построим АФХ данной разомкнутой дискретной системы. Положим 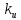=1, .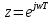







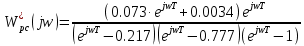w=п/2



w=0

Рисунок 3.3 – АФХ разомкнутой импульсной системы с И-регулятором.






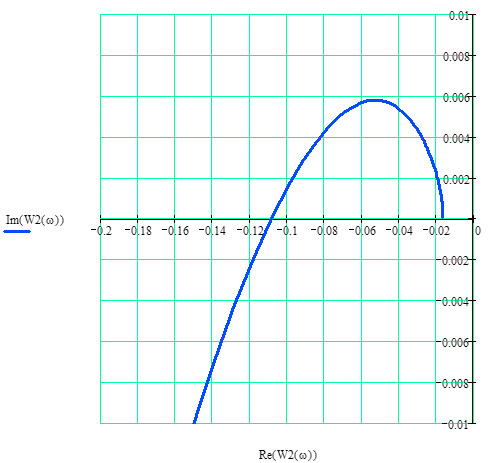
w=п/2



w=0

Рисунок 3.4 – АФХ разомкнутой импульсной системы с И-регулятором (увеличенная)

1   2   3   4   5   6   7

---

3.3. Вывод передаточных функций замкнутой импульсной системы (ЗИС) с типовыми цифровыми регуляторами

(W_о(p) = W_об(p))

1) По каналу задания



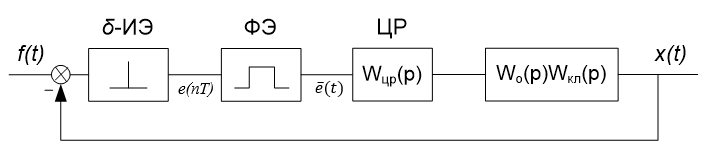
Рисунок 3.5 – Структурная схема импульсной системы по каналу задания.



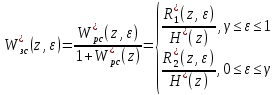Для системы с П-регулятором



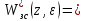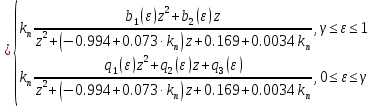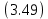При


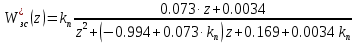Как можно видеть, знаменатель непрерывной передаточной функции не зависит от , поэтому знаменатели непрерывной и дискретной передаточных функций совпадают.

Для системы с И-регулятором



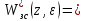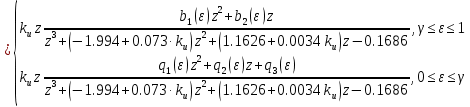При



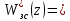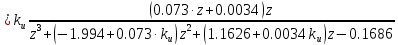Как можно видеть, знаменатель непрерывной ПФ не зависит от , поэтому знаменатели непрерывной и дискретной передаточных функций совпадают.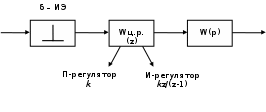

---

3.4. Исследование устойчивости и вычисление критического коэффициента усиления с использованием алгебраического и частотного критериев устойчивости.

Рисунок 3.6 – Структурная схема разомкнутой импульсной системы с цифровым регулятором



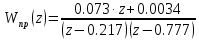
П-регулятор







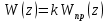
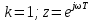
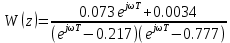
1) Алгебраический критерий







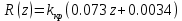
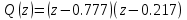
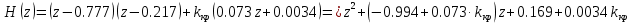
Произведём замену







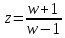
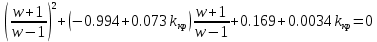
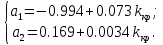
Числитель



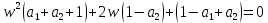
Коэффициенты должны быть положительны









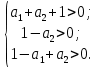
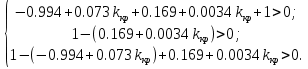
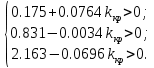
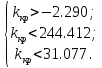
По алгебраическому критерию k_кр = 31.077.

2) Частотный критерий



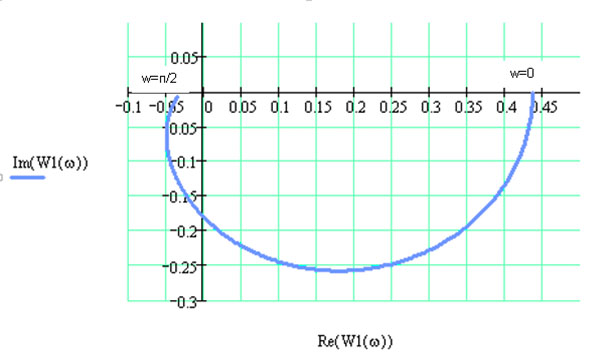
Рисунок 3.7 – График АФХ разомкнутой системы с П-регулятором



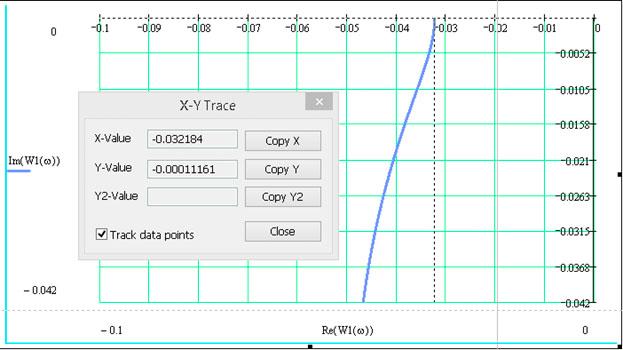
Рисунок 3.8 – График АФХ разомкнутой системы с П-регулятором (приближенный)

Точка пересечения АФХ РС с действительной осью -0.032184. По АФХ определим критический коэффициент усиления. Так как мы строили АФХ при коэффициенте усиления k = 1, тогда



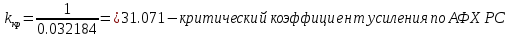
Значения критических коэффициентов по алгебраическому и частотному критериям сошлись, значит, выполнено верно.

---

Дальше будем работать с коэффициентом из области устойчивости k = 1.

И-регулятор







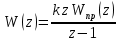
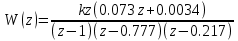
1) Алгебраический критерий







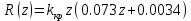
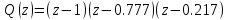
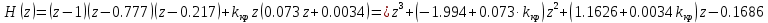
Произведём замену







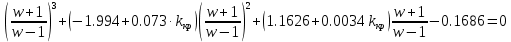
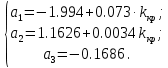
Числитель









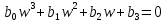
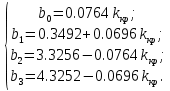
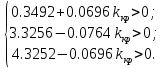
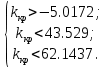
По критерию Раута-Гурвица:







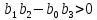
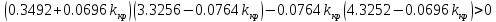
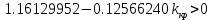
Решая эту систему, находим 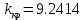и область устойчивости: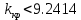



2) Частотный критерий



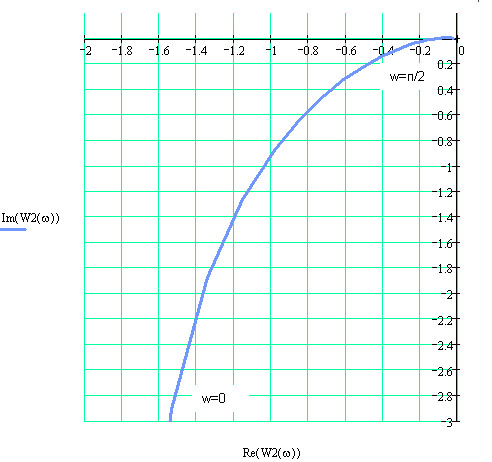
Рисунок 3.9 – График АФХ разомкнутой системы с И-регулятором



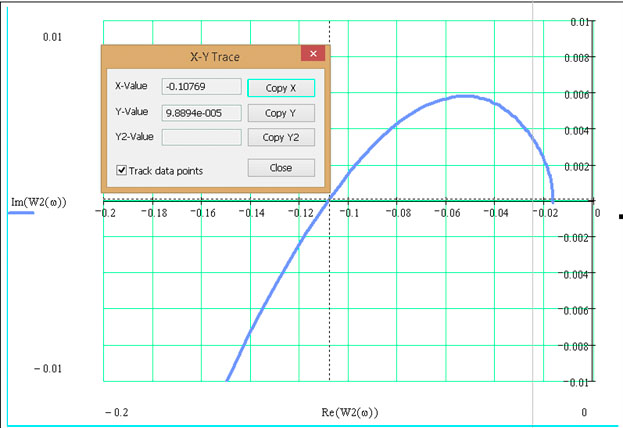
Рисунок 3.10 – График АФХ разомкнутой системы с И-регулятором (приближенный)

Точка пересечения АФХ РС с действительной осью -0.10769. По АФХ определим критический коэффициент усиления. Так как мы строили АФХ при коэффициенте усиления k = 1, тогда



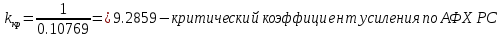
Значения критических коэффициентов по алгебраическому и частотному критериям сошлись, значит, выполнено верно.

Дальше будем работать с коэффициентом из области устойчивости k = 1.

3.5. Исследование показателей качества ЗИС с типовыми регуляторами (

---