Файл: Физикохимические.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 194

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ОБЩАЯ ХАРАКТЕРИСТИКА И КЛАССИФИКАЦИЯ ФИЗИКО­ХИМИЧЕСКИХ МЕТОДОВ АНАЛИЗА

Основной закон светопоглощения (Закон Бугера­Ламберта­Бера)

Основные узлы приборов абсорбционной спектроскопии

Спектрофотометр СФ­ 4

Основные узлы приборов для эмиссионного спектрального анализа

Качественный эмиссионный спектральный анализ

РЕНТГЕНОСПЕКТРАЛЬНЫЙ МЕТОД АНАЛИЗА

Основные узлы рентгеноспектральных приборов

Количественный рентгеноструктурный анализ

Практическое применение Рентгеноспектральные методы анализа имеют разнообразные области применения. В геологии, горном деле, металлургии и гидрометаллургии этим методом определяют состав минералов, руд, и продуктов их переработки ‐ шлаков, концентратов и т. д., устанавливают состав легированных сталей и сплавов, в химических отраслях промышленности (электрохи‐ мии, нефтехимии и т. д.) анализируют исходное сырье и готовую продукцию, в ядерной тех‐ нике контролируют изменения в составе замедлителей, теплоносителей и т. д. Широко ис‐ пользуются рентгеноспектральные методы для анализа керамики, стекла, пластмасс, абра‐ зивов, катализаторов и других материалов сложного химического состава. Весьма эффектив‐ ным оказалось применение рентгеноспектрального флуоресцентного анализа для контроля загрязнением окружающей среды (определение содержания различных элементов в аэро‐ золях, почвах, воде, растительных и животных тканях и т. д.). Например, в аэрозолях опре‐ деляют до 40 элементов от натрия до свинца. Рентгеноспектральный анализ показал, в ча‐ стности, что источником загрязнения атмосферы кальцием служит цементная промышлен‐ ность, свинцом и бромом ‐ выхлопные газы автомобилей и т. д.Широкое применение нашел рентгеноспектральный метод определения толщины по‐ крытий ‐ тонкого слоя, нанесенного на основной материал, как, например, цинка на оцинко‐ ванном железе, слоя ферропорошка на магнитофонной ленте и т. д. Метод основан на ис‐ пользовании градуировочных графиков, показывающих зависимость интенсивности спек‐ тральной линии от толщины покрытия. Градуировочный график строится по стандартам с известной толщиной слоя.Очень эффективным оказалось применение рентгеновского флуоресцентного метода в анализе космических объектов. С помощью спектрометрической аппаратуры РИФМА (рент‐ геновский, изотопный флуоресцентный метод анализа), установленной на «Луноходе‐1», было определено содержание основных породообразующих элементов непосредственно на поверхности Луны. Для возбуждения флуоресцентного излучения применялись радиоактив‐ ные источники, характеризующиеся высокой стабильностью и не нуждающиеся в электри‐ ческой энергии. В качестве детектора использовались пропорциональные счетчики. Элек‐ трический импульс счетчика преобразовывался и по радио передавался на Землю.Широко известны и весьма важны применения рентгеновского излучения во многих других областях науки и техники (определение структуры кристаллов, рентгеновская дефек‐ тоскопия изделий, диагностика заболеваний и т. д.). Общая характеристика метода Методами рентгеноспектрального анализа определяют состав различных сплавов, руд, минералов, цементов, пластмасс и многих других изделий, устанавливают характер за‐ грязнений окружающей среды, анализируют космические объекты и т. д. Он используется для определения больших содержаний (десятки процентов) и небольших примесей (10‐ 2...10‐3 %). Предел обнаружения рентгеноспектральными методами в общем ограничивает‐ ся величинами порядка (10‐2...10‐3 %). Сочетание с химическими методами обработки позво‐ ляет его значительно снизить. Средняя квадратичная погрешность методов составляет при‐ мерно 2...5%, при благоприятных условиях она снижается до

Газовая хроматография

Качественный хроматографический анализ

КОНДУКТОМЕТРИЧЕСКИЙ МЕТОД АНАЛИЗА

Измерение электропроводности растворов

ПОТЕНЦИОМЕТРИЧЕСКИЙ МЕТОД АНАЛИЗА

Измерительная ячейка и электроды потенциометрического ме­ тода анализа.

Приборы для измерения ЭДС гальванического элемента


  1. 1   ...   4   5   6   7   8   9   10   11   ...   22

РЕНТГЕНОСПЕКТРАЛЬНЫЙ МЕТОД АНАЛИЗА

  1. Теоретические основы рентгеноспектрального метода анализа


Быстролетящие частицы, например электроны, могут вызывать возбуждение или иони‐ зацию атомов не только в газообразном состоянии. При столкновении электрона с какой‐ либо твердой поверхностью может также произойти возбуждение или ионизация атомов. Если энергия летящего электрона достаточна, происходит выбивание электрона из внутрен‐ них К‐ или L‐оболочек атомов вещества, подвергающего бомбардировке. На освободившее‐ ся место в К‐ или L‐оболочке переходит электрон с более высокого энергетического уровня, что сопровождается характеристическим рентгеновским излучением.
Кроме характеристического в этом процессе возникает рентгеновское излучение с не‐ прерывным спектром, связанное с частичным превращением энергии тормозящихся элек‐ тронов при столкновении с мишенью в энергию излучения. Это излучение называют тор‐ мозным.

Максимальная частота непрерывного рентгеновского излучения νmax, связана с напряжением V на рент‐ геновской трубке соотношением

eV = hvmax.

Таким образом, эмиссионный рентгеновский спектр представляет собой непрерыв‐ ный фон, перекрытый линиями характеристического излучения. Характеристическое рент‐ геновское излучение наблюдается не только при бомбардировке электронами, оно возника‐ ет также при облучении поверхности электромагнитным излучением большой энергии, дос‐ таточной для выбивания внутренних электронов из атомов. Излучение непрерывного спек‐ тра при этом не происходит, и характеристический спектр, полученный таким способом, на‐ зывается флуоресцентным или вторичным.
Следует отметить, однако, что внутриатомный переход электрона с верхнего энергетического уровня на К‐ или L‐уровень не всегда сопровождается характеристическим рентгеновским излучением. Возможен и бе‐ зызлучательный переход. При этом происходит перестройка электронной оболочки и один из внешних элек‐ тронов отрывается от атома. Этот процесс известен как
эффект 0же, а электроны, отрывающиеся от атома, называют оже ‐ электронами. Вероятность проявления эффекта Оже во многих случаях очень велика, а у лег‐ ких элементов она даже больше, чем вероятность рентгеновского излучения, что вызывает определенные трудности в рентгеноспектральном анализе легких элементов.


  • Рентгеновские термы. Линии характеристического рентгеновского излучения со‐ ответствуют разности энергетических уровней внутренних электронных оболочек атома. Час‐ тоты характеристического излучения атомов данного элемента могут быть рассчитаны по уравнению

2π2me4F2 1 1

2 1 1

v = h3 (n2 — n2) = RF (n2 — n2) (5.1.1)

1 2 1 2

Здесь F ‐ эффективныйзарядядра, равный

F = Z — σ,

где Z‐ заряд ядра, равный порядковому номеру элемента в периодической системе Д. И. Менделеева; σ‐ постоянная экранирования.

Вместо уравнения (5.1.1) можно записать


R(Z — σ)2 R(Z — σ)2



Величину

v = 2 —


n
1

2 = T1 — T2. (5.1.2)


n
2

R(Z — σ)2
(5.1.3)

T = n2 .

называют рентгеновскимтермом.

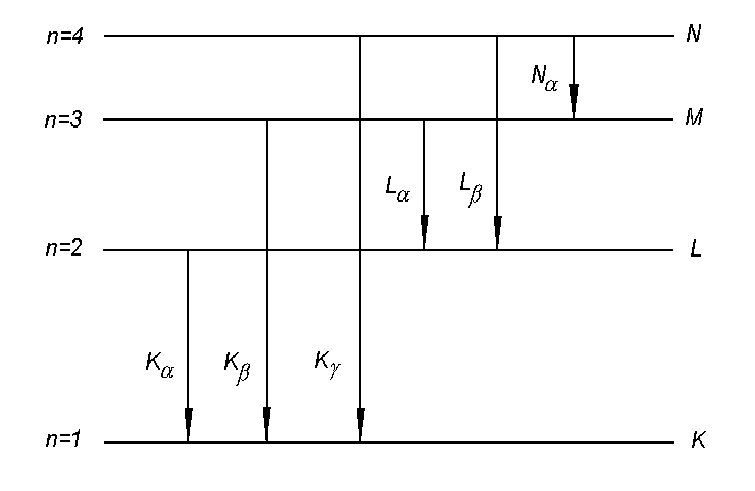Символика, используемая для обозначения и классификации линий рентгеновского спектра, схематично приведена на рисунке 5.1.1. Для учета подуровней у символа линии ста‐ вят числовой индекс, например, Kα1,Kβ2 и т. д. Число линий в рентгеновском спектре сравни‐

тельно невелико. В соответствии с

законом Мозли квадратный корень из волнового числа (или частоты) первой К‐линии связан с порядко‐ вым номером элемента в периоди‐ ческой системе линейной зависимо‐ стью:


Рисунок 5.1.1 - Схема электронных переходов рентгенов- ского спектра: n=1,2,3,4 - главные квантовые числа; K,L,M,N - электронные оболочки

√v = K(Z — σ). (5.1.4)

График зависимости Z от ν представляет собой прямую. С открытием закона Мозли порядковый номер элемента в периодиче‐ ской системе получил четкое физическое истолкование как заряд ядра. Поскольку характеристические линии рентгеновского спектра при переходе от одного элемента к другому смещаются на одну и ту же вели‐

чину, это свойство позволяет установить, имеется ли между двумя элементами периодической системы какой‐ то третий, еще неизвестный, и предсказать его рентгеновский спектр. Замечательным практическим примене‐ нием закона Мозли было его использование при открытии предсказанных Д. И. Менделеевым элементов пе‐ риодической системы (гафния и рения).

Часто наблюдается прямая пропорциональность между интенсивностью линии I и концентрацией элемента C в пробе I=kC. Однако факторов влияющих на интенсивность линий рентгеновского спектра много. Точная оценка величин, оказывавших влияние на ин‐ тенсивность спектральной линии, очень сложна. Более надежны данные, так же как и в оп‐ тической эмиссионной спектроскопии, полученные по относительной интенсивности двух спектральных линий, находящихся в одной и той же области длин волн.

Интенсивность линий рентгеновского спектра зависит от распределения бомбардирующих электронов по скоростям или от распределения интенсивности в спектре возбуждающего излучения в случае флуорес‐ центных спектров. При одинаковых условиях интенсивность характеристических линий спектра максимальна, когда максимальная интенсивность источника возбуждения соответствует энергии возбуждения данной линии. Интенсивность спектра зависит также от числа излучающих атомов, вероятности излучательного перехода и некоторых других факторов.

Ослабление рентгеновского излучения при прохождении через пробу подчиняется за‐ кону светопоглощения

I = I0 · 10–μρl,

где I0и I ‐ интенсивность падающего и прошедшего через пробу рентгеновского излучения соответственно;  ‐ массовый коэффициент поглощения; l‐ толщина слоя;  ‐ плотность ве‐ щества.

    1. 1   ...   5   6   7   8   9   10   11   12   ...   22

Смотрите также файлы