Файл: Учебное пособие для практических занятий по дисциплине Финансовый менеджмент.doc

Погашение суммы долга равными срочными уплатами

При использовании сложных процентов при условии, что платежи в счет погашения кредита производятся один раз в конце каждого года в течение n-лет из расчета g - % годовых, срочная уплата определяется по формуле:

(1.41)

где – коэффициент приведения постоянной годовой ренты. Определяется по формуле:

(1.42)

Если выплаты по кредиту будут производиться несколько раз ( -раз) в году, проценты будут начисляться также несколько раз (m- раз) в году, то срочную уплату можно определить по формуле:

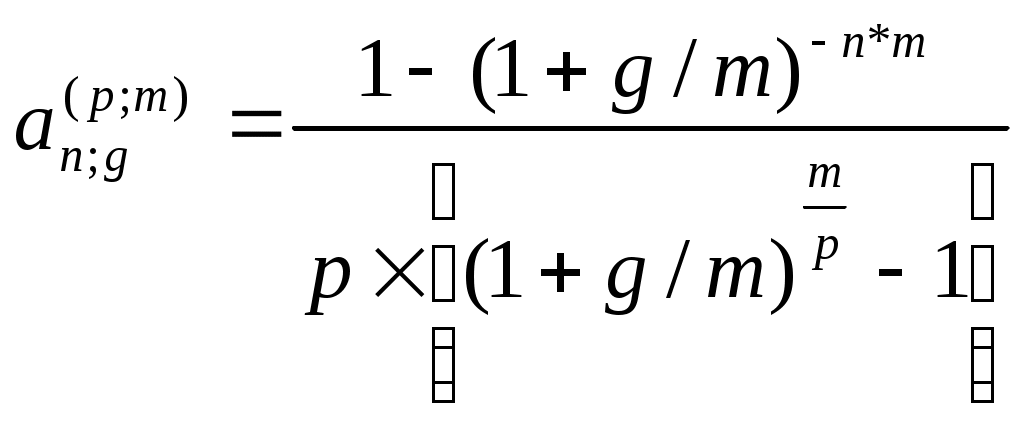(1.43) (1.44)

Задача 1.10. Разработать план-график погашения кредита (в форме таблицы) по следующим условиям: сумма контракта – 10,5 млн. руб.; авансовый платеж – 1 млн. руб.; срок кредита - 6 лет; ставка процента за кредит – 7% годовых. Погашение кредита должно производиться равными срочными уплатами.
Решение

Срочную уплату определяем по формуле:

(1.41) (1.42)

= 4,76654

= (10500 – 1000) / 4,76654 = 1993 (тыс. руб.)

Срочная уплата (графа 3) включает набежавшие проценты на остаток долга, которые выплачиваются в первую очередь (графа 4), и оставшейся части платежа, которая идет в счет погашения основного долга (графа 5).
Таблица 1.3 - План- график погашения кредита

равными срочными уплатами, тыс. руб.

Номер года	Долг на начало года	Срочная уплата			Остаток долга на конец года
		Всего	в том числе
			% за кредит	часть долга
1	2	3	4 = гр.2*g	5 = гр.3-гр.4	6 = гр.2 - гр.5
1	9500	1993	9500*0,07=665	1993-665=1328	9500-1328=8172
2	8172	1993	8172*0,07=572	1421	6751
3	6751	1993	473	1520	5231
4	5231	1993	366	1627	3604
5	3604	1993	252	1741	1863
6	1863	1993	130	1863	0
Итого		11958	2458	9500

---

PS. При необходимости устранения недоплаты или переплаты делается корректировка последнего платежа.

Частичные платежи любыми суммами актуарным методом

Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга. Частичный платеж идет, в первую очередь, на погашение процентов, накопленных на дату частичного платежа. Если величина платежа превышает сумму начисленных процентов, то разница идет на погашение основной суммы долга. Непогашенный остаток долга служит базой для начисления процентов за период до следующей уплаты. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Этот платеж будет приплюсован к следующему платежу.
Частичные платежи любыми суммами по правилу торговца

1. Если срок ссуды не превышает год, то сумма долга с начисленными за весь срок процентами остается неизменной до полного погашения. Параллельно идет накопление сумм частичных платежей с начисленными на них процентами за период от даты очередного платежа до даты погашения всего долга. Последний платеж должен балансировать долг и платежи и определяется вычитанием одной суммы из другой.

2. Если срок ссуды превышает год, то указанные выше расчеты ведутся для годового периода задолженности. В конце года из наращенной суммы долга вычитается наращенная сумма частичных платежей. Полученный остаток погашается в следующем году.

В качестве примечания отметим, что при использовании актуарного метода сумма платежей в счет погашения долга будет несколько выше, чем по правилу торговца.
Задача 1.11. Долг в сумме 15 млн. руб. необходимо погасить в течение полутора лет за период с 12 марта 2018 г. по 12 сентября 2019 г. Кредитор согласен получать частичные платежи. Проценты начисляются по ставке 20 % годовых по формуле простых процентов. Частичные поступления характеризуются следующими данными:

• 
  12 июня 2018 г. - 500 тыс. руб.;
  
• 
  12 июня 2019 г. - 5000 тыс. руб.;
  
• 
  30 июня 2019 г. - 8000 тыс. руб.;
  
• 
  12 сентября 2019 г. – S_о. =5594.5
  
• 
  Определить сумму последнего платежа (S_о) актуарным методом.
  

12.03.18 12.06.18 12.06.19 30.06.19 1.07 1.08 1.09 12.09.19

/-----------/---------------------/-----------------/-------|------|--------|-----------/

---

3 мес 12 мес 30-12=18дней 0+30+30+12=72дня

Решение

Для решения задачи составим уравнение, отражающее последовательность выполняемых действий по погашению кредита. Решение этого уравнения даст искомый результат – сумму последнего платежа. В расчетах используем простые проценты и германскую практику. На 12 июня 2018 г., дату первого платежа наращенная сумма долга составит:

S₁ = (((15000 * (1 + 3/12 * 0,2)) = 15750 тыс. руб.

Отметим, что первый платеж в сумме 500 тыс. руб. меньше суммы начисленных за этот период процентов (750 тыс. руб.), поэтому этот платеж долг не уменьшает и будет присоединен ко второму платежу. Расчет начинаем снова (от даты выдачи кредита) и определяем наращенную сумму долга на дату второго платежа 12 июня 2019 г. (период наращения составит 15 месяцев или 15/12 года). Вычитаем из наращенной суммы произведенные выплаты – 500 и 5000 тыс. руб. Затем определяем наращенную сумму остатка долга на 30 июня 2019 г. - период наращения - 18 дней или 18/360 года. Из этой суммы вычитаем третий платеж в сумме 8000 тыс. руб. и определяем наращенную сумму долга на 12 сентября 2019 г. – период наращения 73 дня или 73/360 года.

Sо = (((15000 * (1 + 15/12 *0,2) – (500 + 5000)) * (1 + 18/360 * 0,2) – 8000) * (1 + 72/360 * 0,2) = 5594,5 (тыс. руб.)

Ответ: 5594,5 тыс. руб.
Задача 1.12. Обязательство в сумме 1, 5 млн. руб., датированное 10 августа 2018 г. и выданное под 20% годовых, должно быть погашено 10 июня 2019 г. частичными платежами. В счет погашения долга 10 декабря 2018 г. было выплачено 800 тыс. руб. Определить остаток долга на конец срока актуарным методом и по правилу торговца.

10/08 10/12 10/06

|---------------------------|-----------------------------|

4/12 6/12

Решение

Составим уравнение, отражающее порядок расчетов соответствующим методом. Отличия только в определении периода наращения:

- для актуарного метода период наращения определяется как интервал времени до даты очередного платежа;

S_oа = (1,5 * (1 + 4/12 *0,2) – 0,8) * (1 + 6/12 *0,2) = 0,88 млн. руб.

- по правилу торговца период наращения определяется от даты очередного платежа до даты полного погашения долга;

S_oт = 1,5 * (1 + 10/12 *0,2) – 0,8 * (1 + 6/12 *0,2) = 0,87 млн. руб.
С целью обеспечения гарантий и ответственности за своевременное выполнение обязательств по кредитам могут предусматривать специальные меры имущественного характера:

1. Неустойка, которую должник обязан уплатить кредитору в случае неисполнения или ненадлежащего исполнения обязательства.

2. Залог, т.е. выделение из имущества должника определенной его части, за счет которой будут удовлетворены требования залогодержателя в случае невозврата кредита в срок. Самый надежный вид залога – недвижимость.

---

3. Удержание кредитором вещи, подлежащей передаче должнику.

4. Привлечение к обязательству третьих лиц и их имущества (например, поручительство физического или юридического лица или банковская гарантия исполнения должником обязательств).

5. Денежный задаток и т.д.

2. ИЗМЕНЕНИЕ УСЛОВИЙ ПЛАТЕЖЕЙ ПО ФИНАНСОВЫМ ОБЯЗАТЕЛЬСТВАМ
Наиболее часто предлагается: изменить сроки платежей в сторону их увеличения, произвести объединение нескольких платежей в один (консолидировать платежи) с установлением единого срока погашения, изменить условия погашения кредитов (конверсия займов) и т.п. Основным принципом изменения условий сделки (контракта) является принцип финансовой эквивалентности, который заключается в том, что сумма заменяемых платежей, приведённых к какой - то определённой дате, должна быть равна сумме платежей по новому обязательству, приведенных к той же дате.

2.1. Частный случай консолидации платежей
Если срок уплаты консолидированного платежа находится в интервале старых сроков, т.е. , то величину консолидированного платежа определяют по формуле:

(2.1)

где – суммы консолидируемых платежей, сроки погашения которых меньше срока уплаты консолидированного платежа ;

– суммы платежей со сроками уплаты, превышающими срок уплаты консолидированного платежа - . Соответственно (2.2), (2.3)
Задача 2.1. Фирма в погашение задолженности банку за предоставленный под 15% годовых (простые проценты) кредит, полученный 01.ХХ.ХХ должна произвести три платежа: 2 млн. руб., 2.7 млн. руб. и 3.3 млн. руб. в сроки, соответственно, 20.04., 25.05., 15.06. Фирма предложила банку объединить все платежи в один и погасить его 01.06.ХХ Определить размер консолидированного платежа.

---

Решение

В расчетах используем английскую практику начисления простых процентов. С помощью таблицы «Порядковые номера дней в году» определим порядковые номера дней уплаты: 20.04. –110 день в году; 25.05. – 145 день; 01.06. – 152 день;15.06. – 166 день.

Соответственно, периоды наращения для платежей, находящихся слева от даты 1 июня (2 и 2,7 млн. руб.) и периоды дисконтирования для платежей, находящихся справа от даты 1 июня (3,3 млн. руб.) для приведения к 01 июня составляют:

₁ = 152 –110 = 42 дня ₂ = 152 –145 = 7 дней ₃ = 166 – 152 = 14 дней

Сумма погашения консолидированного платежа определится по формуле:

(2.1)

S_o = 2,0 * (1 + 42/365 *0,15) + 2,7 *(1 + 7/365 *0,15) + 3,3 * (1 + 14/365 *0,15)^-1 = 8,023 (млн. руб.)

Ответ: 8,023 млн. руб.
Если партнёры заранее оговаривают сумму консолидированного платежа, то необходимо определить срок его уплаты, сохраняя принцип финансовой эквивалентности обязательств.

При использовании простых процентов срок уплаты консолидированного платежа ( ) определяется по формуле:

(2.4)

где – сумма консолидированного платежа;

– процентная ставка, используемая при консолидации.

– современная величина платежей, подлежащих консолидации. Определяется по формуле математического дисконтирования:

(2.5)
Задача 2.2. Фирма имеет ряд финансовых обязательств перед одним кредитором – 2,5 млн. руб., 3,1 млн. руб. и 2,7 млн. руб., которые должна погасить через 40, 70 и 160 дней после 01.01 текущего года. По согласованию сторон решено заменить их одним платежом, равным 9 млн. руб., с продлением срока оплаты, используя процентную ставку 12%. Найти срок уплаты консолидированного платежа

---