Файл: Курсовой проект по Детали машин и основы конструирования наименование дисциплины.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 92
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3 РАСЧЕТ БЫСТРОХОДНОЙ ЦИЛИНДРИЧЕСКОЙ КОСОЗУБОЙ ПЕРЕДАЧИ РЕДУКТОРА
4 РАСЧЕТ ОТКРЫТОЙ КОНИЧЕСКОЙ ПЕРЕДАЧИ
4.5 Выбор материала и расчет допускаемых напряжений
4.7 Проверка зубьев колёс по напряжению изгиба
4.8 Проверка зубьев колёс по контактным напряжениям
5 ПРЕДВАРИТЕЛЬНЫЙ РАСЧЕТ ВАЛОВ РЕДУКТОРА
5.5 Расчет промежуточного вала
6 ПРЕДВАРИТЕЛЬНЫЙ ПОДБОР ПОДШИПНИКОВ НА ВАЛЫ РЕДУКТОРА
7 ПОДБОР И РАСЧЕТ ШПОНОЧНЫХ СОЕДИНЕНИЙ
7.4 Подбор и расчет шпоночных соединений
8 ПРОВЕРОЧНЫЙ РАСЧЁТ ВАЛОВ РЕДУКТОРА
8.5 Построение схемы промежуточного вала
8.6 Реакции опор в плоскости XOZ
8.7 Реакции опор в плоскости XOY
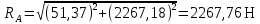
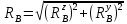| |  | (8.18) |
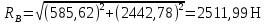
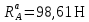
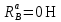
8.9 Эпюры изгибающих моментов
Строим эпюры изгибающих моментов в плоскости XOZ.
1 участок: 0 ≤ x1 ≤ l1.
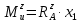| |  | (8.19) |
При x1 = 0:
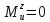
При x1 = l1 = 34,11 мм:
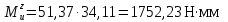
2 участок: 0 ≤ x2 ≤ l2.
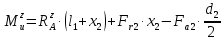| |  | (8.20) |
При x2 = 0:
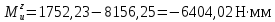
При x2 = l2 = 55,24 мм:
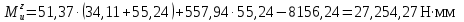
3 участок: 0 ≤ x3 ≤ l3.
| |  | (8.21) |
При x3 = 0:
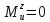
При x3 = l3 = 46,45 мм:
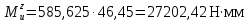
Строим эпюры изгибающих моментов в плоскости XOY.
1 участок: 0 ≤ x1 ≤ l1.
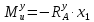| |  | (8.22) |
При x1 = 0:
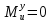
При x1 = l1 = 34,11 мм:
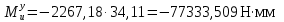
2 участок: 0 ≤ x2 ≤ l2.
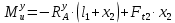| |  | (8.23) |
При x2 = 0:
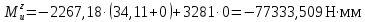
При x2 = l2 = 55,24 мм:
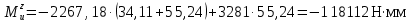3 участок: 0 ≤ x3 ≤ l3.| | 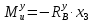 | (8.24) |
При x3 = 0:
При x3 = l3 = 46,45 мм:
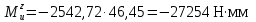
Строим суммарную эпюру.
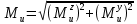| |  | (8.25) |
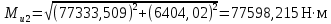
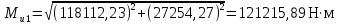
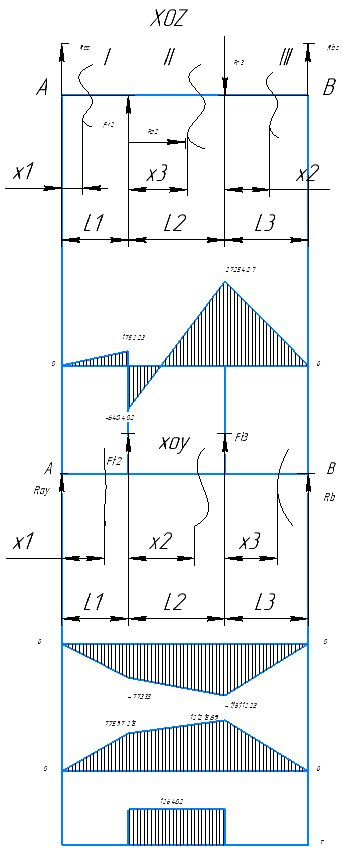
Рисунок 8.4 – Эпюры изгибающего момента на промежуточном валу
+
8.10 Проверочный расчёт вала
Выполним проверочный расчёт вала на статистическую прочность под шестерней.
Механические характеристики стали 40Х (табл. 12.8 [1]):
σT = 640 H/мм2;
σB = 790 H/мм2;
τT = 380 H/мм2;
d = 32 мм – диаметр вала под шестерней;
KП = 2,2 – коэффициент перегрузки (табл. 19.28 [1]).
Определим нормальное напряжение в рассматриваемом сечении при действии максимальных нагрузок по формуле (с 274 [1]):
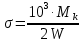| |  | (8.26) |
где Mmax – суммарный изгибающий момент. Н·м;
W– момент сопротивления сечения вала при изгибе, мм3;
Fmax– осевая сила, Н;
Определим касательное напряжение в рассматриваемом сечении при действии максимальных нагрузок по формуле (с 274 [1]):
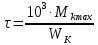| |  | (8.27) |
где MKmax– крутящий момент, Н·м;
WK – момент сопротивления сечения вала при кручении, мм3.
Суммарный изгибающий момент рассчитываем по формуле (с 274 [1]):
Момент сопротивления при изгибе рассчитываем по формуле (с 275 [1]):
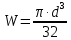| |  | (8.30) |
Момент сопротивления при кручении рассчитываем по формуле (с 275 [1]):
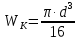| |  | (8.31) |
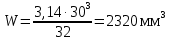
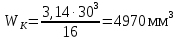
По формуле 8.26 определим нормальное напряжение в рассматриваемом сечении при действии максимальных нагрузок:
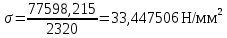
По формуле 8.27 определим касательное напряжение в рассматриваемом сечении при действии максимальных нагрузок:
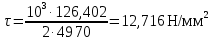
Частный коэффициент запаса прочности при нормальном напряжении (с 274 [1]):
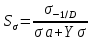| |  | (8.34) |
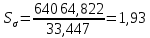
Частный коэффициент запаса прочности при касательном напряжении (с 274 [1]):
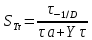| |  | (8.35) |
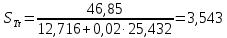
Общий коэффициент запаса прочности по пределу текучести рассчитываем по формуле (с 274 [1]):
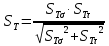| |  | (8.36) |
Статистическую прочность можно считать обеспеченной если выполнено условие (с 274 [1]):
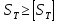| |  | (8.37) |
где [ST] – минимально допустимое значение, [ST] =1,4 (с 274 [1]).
Условие 8.37 выполнено, следовательно, статистическая прочность вала обеспечена.
Выполним расчёт на сопротивление усталости вала под шестерней.
Коэффициент запаса прочности в сечении вычисляется по формуле (с 280 [1]):
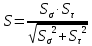| |  | (8.38) |
Условие обеспечения прочности в сечении (с 280 [1]):
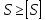| |  | (8.39) |
где [S] – минимально допустимая прочность