Файл: Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 158
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. ЦЕЛЬ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
2.1 Лабораторная работа 1. «Теория погрешностей и машинная арифметика»
2.2 Лабораторная работа 2. « Решение нелинейных уравнений»
2) Расчетные формулы методов решения нелинейного уравнения .
2.3 Лабораторная работа 3. « Интерполирование функций»
2.6 Лабораторная работа 6. «Методы численного интегрирования функций»
требуют использования специальных методов, ориентированных на данный узкий класс задач.
2. Контрольные вопросы
3. Практические задания
Методом Рунге-Кутта (2-го или 4-го порядка точности) найдите решение системы дифференциальных уравнений на отрезке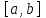 при начальных условиях с шагом
при начальных условиях с шагом 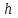 . Шаг выбрать самостоятельно. Численные решения
. Шаг выбрать самостоятельно. Численные решения 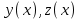 представьте графически. Сравните с аналитическим решением, если его можно найти.
представьте графически. Сравните с аналитическим решением, если его можно найти.
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 7.
1.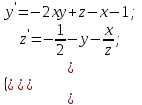
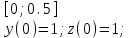
2.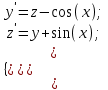
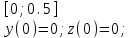
3.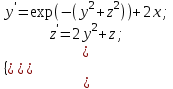
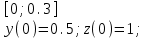
4.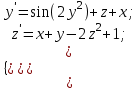
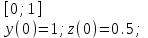
5.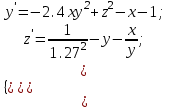
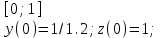
6.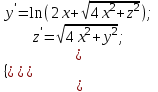
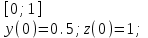
7.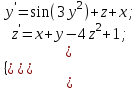
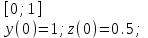
8.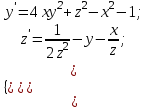
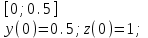
9.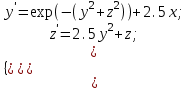

10.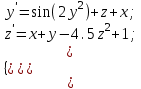

11.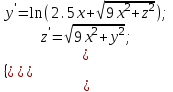

12.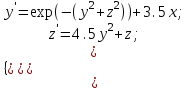

13.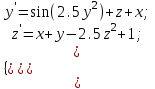

14.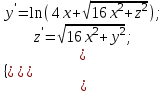

2. Контрольные вопросы
-
Как описываются обыкновенные дифференциальные уравнения? -
Перечислите основные типа задач для обыкновенных дифференциальных уравнений. -
Опишите задачу Коши. -
Что из себя представляют численные методы решения дифференциального уравнения? -
Опишите классы численных методов решения дифференциального уравнения -
Опишите алгоритм метода Рунге-Кутта задача Коши. -
Как оценивается погрешность приближенного решения обыкновенного дифференциального уравнения, полученного методом Рунге-Кутта второго порядка точности на одном шаге? -
Назовите достоинства схемы Рунге-Кутта.
3. Практические задания
Методом Рунге-Кутта (2-го или 4-го порядка точности) найдите решение системы дифференциальных уравнений на отрезке
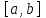 при начальных условиях с шагом
при начальных условиях с шагом 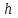 . Шаг выбрать самостоятельно. Численные решения
. Шаг выбрать самостоятельно. Численные решения 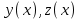 представьте графически. Сравните с аналитическим решением, если его можно найти.
представьте графически. Сравните с аналитическим решением, если его можно найти.ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 7.
1.
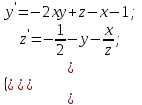
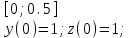
2.
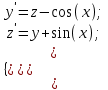
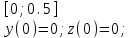
3.
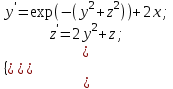
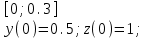
4.
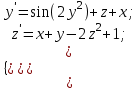
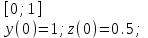
5.
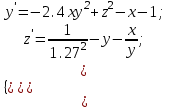
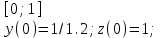
6.
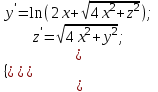
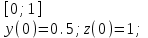
7.
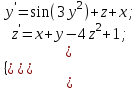
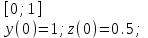
8.
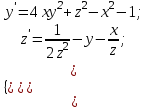
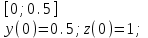
9.
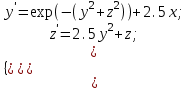

10.
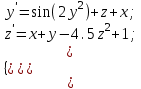

11.
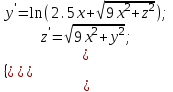

12.
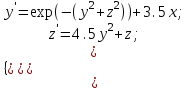

13.
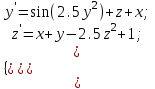

14.
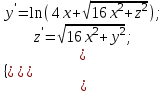

Рекомендуемая литература
-
Зенков А.В.. Численные методы: учеб. пособие для прикладного бакалавриата.- М.: Изд-во Юрайт, 2019.- 122с.- ISBN 978-5-534-10893-4 -
Пирумов У.Г. Численные методы: учебник и практикум для академического бакалавриата. - М.: Изд-во Юрайт, 2019.- 421с.-ISBN 978-5-534-03141-6 -
Пименов В.Г. Численные методы. В 2 ч.: учеб. пособие для вузов - М.: Изд-во Юрайт, 2019; Екатеринбург: Изд-во Урал. ун-та.-111 с. и 106с.- ISBN 978-5-534-10886-6(Ч.1); ISBN 978-5-534-10891-0(Ч.2). -
Зализняк В.Е. Численные методы. Основы научных вычислений: учебник и практикум для академического бакалавриата. - М.: Изд-во Юрайт, 2019.- 356с.- ISBN 978-5-534-02714-3 -
Гателюк О.В. Численные методы: учеб. пособие для академического бакалавриата.- М.: Изд-во Юрайт, 2019.- 140с.- ISBN 978-5-534-05894-9 -
Абрамкин Г.П. Численные методы: учеб. пособие - Изд-во Алтайского гос.пед. ун-та, 2016.-260с.- ISBN 978-5-88210-829-7 -
Семакин, И.Г. Программирование, численные методы и математическое моделирование: учебное пособие / Семакин И.Г., Русакова О.Л., Тарунин Е.Л., Шкарапута А.П. — Москва : КноРус, 2017. — 298 с. — (для бакалавров). — ISBN 978-5-406-00862-1.