Файл: Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 160
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. ЦЕЛЬ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
2.1 Лабораторная работа 1. «Теория погрешностей и машинная арифметика»
2.2 Лабораторная работа 2. « Решение нелинейных уравнений»
2) Расчетные формулы методов решения нелинейного уравнения .
2.3 Лабораторная работа 3. « Интерполирование функций»
2.6 Лабораторная работа 6. «Методы численного интегрирования функций»
N=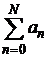 и найти величину абсолютной и относительной погрешностей погрешностей при значениях N=10, 102, 103, 104, 105. Построить гистограммы зависимости погрешностей и количества верных цифр результата от N.
и найти величину абсолютной и относительной погрешностей погрешностей при значениях N=10, 102, 103, 104, 105. Построить гистограммы зависимости погрешностей и количества верных цифр результата от N.
Аналитическое решение задачи (только если не получилось в Mathcad):
SN=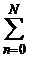
 =
= 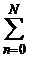
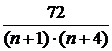
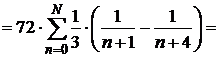
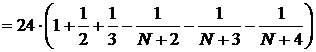 ,
,
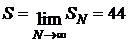 . ОТВЕТ: S =
. ОТВЕТ: S =
 = 44.
= 44.
Теоретический материал. Пусть - точное значение, - приближенное значение некоторой величины. Абсолютной погрешностью приближенного значения называется величина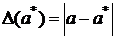 . Относительной погрешностью значения (при 0) называется величина
. Относительной погрешностью значения (при 0) называется величина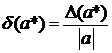 . Так как значение как правило неизвестно, чаще получают оценки погрешностей вида:
. Так как значение как правило неизвестно, чаще получают оценки погрешностей вида: 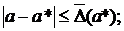
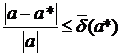 . Величины
. Величины 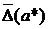 и
и 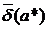 называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
Значащую цифру числа называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Введем функцию S(N)=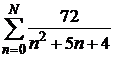 . Тогда абсолютную погрешность можно определить с помощью функции d(N) =
. Тогда абсолютную погрешность можно определить с помощью функции d(N) =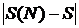 .
.
Вычисления в MATHCAD приведены в файле «таком-то» (см. фрагмент программы на MATHCAD)
Указание. Предварительно ознакомьтесь с форматами представления результатов.
Результаты вычислительного эксперимента:
Здесь следует описать, как вы определили количество верных цифр.
Вывод: сформулировать самостоятельно.
Задача 2. Постановка задачи: для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон.
Искомые величины в MATHCAD найдены методом простого перебора.
Выводы сформулировать самостоятельно.
Фрагмент текста программы в системе MATHCAD:

Примеры решения задач
Задача 1.
Округлить сомнительные цифры приближенного числа x с относительной погрешностью d, оставив в его записи только верные цифры. x = 42.221, d = 0.5%.
Решение:
1) Найдем количество верных цифр числа x:
Отсюда n = 3
2) Округляем x до трех цифр
x = 42.2
Задача 2.
Записать формулу для оценки абсолютной погрешностей функции трех переменных:
, если
Решение:
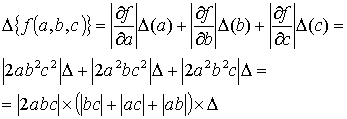
Задача 3.
Дано точное число b и приближенное число x с погрешностью . Указать правило оценки абсолютной и относительной погрешностей функции:
Решение:
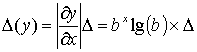
Задача 4.
Дано число a = 547.78, определенное с абсолютной погрешностью . Определить количество верных цифр числа а.
Решение:
1) Найдем относительную погрешность числа
2) Найдем количество верных цифр
. Отсюда n = 4, a = 547.8
Задача 1. Дан ряд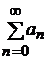 (см. ПРИЛОЖЕНИЕ 1). Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда
(см. ПРИЛОЖЕНИЕ 1). Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда 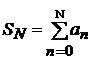 и найти величину погрешности при значениях N=10, 102, 103, 104, 105.
и найти величину погрешности при значениях N=10, 102, 103, 104, 105.
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1. Найти сумму ряда S аналитически как предел частичных сумм ряда (см контрольный пример) или с использованием средств MATHCAD.
2. Используя функцию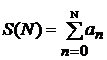
, вычислить значения частичных сумм ряда при указанных значениях N.
3. Для каждого N вычислить величину абсолютной погрешности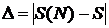 , относительную погрешность d и определить количество верных цифр в S(N)
, относительную погрешность d и определить количество верных цифр в S(N)
4. Представить результаты в виде гистограмм.
Задача 2 . Дана функция f(a,b,c) (см. ПРИЛОЖЕНИЕ 1). Значения переменных указаны в варианте со всеми верными цифрами. Оценить погрешность результата, используя: a) оценки погрешностей для арифметических операций; b) общую формулу погрешностей. Результат представить в двух формах записи: с явным указанием погрешностей и с учетом верных цифр.
Задача 3. Для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон (см. контрольный пример).
ПРИЛОЖЕНИЕ 1
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 1
Аналитическое решение задачи (только если не получилось в Mathcad):
SN=
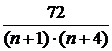
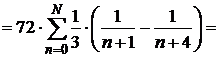
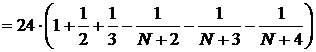 ,
, Теоретический материал. Пусть - точное значение, - приближенное значение некоторой величины. Абсолютной погрешностью приближенного значения называется величина
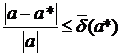 . Величины
. Величины Значащую цифру числа называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Введем функцию S(N)=
Вычисления в MATHCAD приведены в файле «таком-то» (см. фрагмент программы на MATHCAD)
Указание. Предварительно ознакомьтесь с форматами представления результатов.
Результаты вычислительного эксперимента:
| Частная сумма | Абсолютная погрешность | Относительная погрешность | Верные цифры числа |
| S(10)=38.439560439 | 6 | 0.1 | 4  101 101 |
| S(100)=43.3009269 | 0.7 | 0.02 | 43 |
| S(1000)=43.9282153 | 0.07 | 0.002 | 43.9 |
| S(10000)=43.992802 | 0.007 | 0.0002 | 43.99 |
| S(100000)=43.9992802159957 | 0.0007 | 0.00002 | 43.999 |
Здесь следует описать, как вы определили количество верных цифр.
Вывод: сформулировать самостоятельно.
Задача 2. Постановка задачи: для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон.
Искомые величины в MATHCAD найдены методом простого перебора.
Выводы сформулировать самостоятельно.
Фрагмент текста программы в системе MATHCAD:

Примеры решения задач
Задача 1.
Округлить сомнительные цифры приближенного числа x с относительной погрешностью d, оставив в его записи только верные цифры. x = 42.221, d = 0.5%.
Решение:
1) Найдем количество верных цифр числа x:
Отсюда n = 3
2) Округляем x до трех цифр
x = 42.2
Задача 2.
Записать формулу для оценки абсолютной погрешностей функции трех переменных:
, если
Решение:
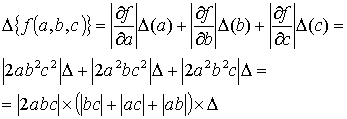
Задача 3.
Дано точное число b и приближенное число x с погрешностью . Указать правило оценки абсолютной и относительной погрешностей функции:
Решение:
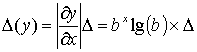
Задача 4.
Дано число a = 547.78, определенное с абсолютной погрешностью . Определить количество верных цифр числа а.
Решение:
1) Найдем относительную погрешность числа
2) Найдем количество верных цифр
. Отсюда n = 4, a = 547.8
-
Контрольные вопросы
-
Дайте определения приближенного числа, абсолютной и относительной погрешности. -
Какие цифры для заданного приближенного числа являются значащими? Приведите примеры. -
Какие цифры для заданного приближенного числа являются верными? Приведите примеры. -
Какие цифры для заданного приближенного числа являются сомнительными? Приведите примеры. -
Обозначьте связь относительной погрешности с количеством верных знаков числа -
Как определяется погрешность арифметических действий? -
Объясните общую формулу вычисления погрешности. -
Опишите форму представления чисел в ЭВМ. -
Дайте определения машинной бесконечности, машинного эпсилона, границы относительной погрешности. Опишите способы их определения. -
Как оценивается величина относительной погрешности?
-
Практические задания
Задача 1. Дан ряд
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1. Найти сумму ряда S аналитически как предел частичных сумм ряда (см контрольный пример) или с использованием средств MATHCAD.
2. Используя функцию
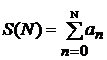
, вычислить значения частичных сумм ряда при указанных значениях N.
3. Для каждого N вычислить величину абсолютной погрешности
4. Представить результаты в виде гистограмм.
Задача 2 . Дана функция f(a,b,c) (см. ПРИЛОЖЕНИЕ 1). Значения переменных указаны в варианте со всеми верными цифрами. Оценить погрешность результата, используя: a) оценки погрешностей для арифметических операций; b) общую формулу погрешностей. Результат представить в двух формах записи: с явным указанием погрешностей и с учетом верных цифр.
Задача 3. Для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон (см. контрольный пример).
ПРИЛОЖЕНИЕ 1
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 1
Таблица к задаче 1
| N | | N | | N | |
| 1 | | 11 | 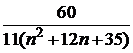 | 21 | 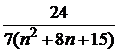 |
| 2 | 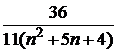 | 12 | 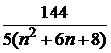 | 22 | |
| 3 | | 13 | | 23 | |
| 4 | 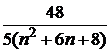 | 14 | | 24 | |
| 5 | 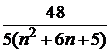 | 15 | | 25 | |
| 6 | 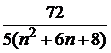 | 16 | | 26 | |
| 7 | | 17 | | 27 | |
| 8 | | 18 | | 28 | |
| 9 | 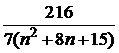 | 19 | | 29 | |
| 10 | 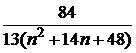 | 20 | 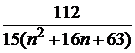 | 30 | 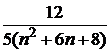 |
Таблица к задаче 2
| № | | | | | № | | | | |
| 1 | | 0.0125 | 0.283 | 0.0187 | 16 | 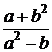 | 4.41 | 18.5 | |
| 2 | | 14.29 | 13.81 | 10.98 | 17 | | 16.5 | 4.2 | |
| 3 | | 12.28 | 13.21 | 12.19 | 18 | | 52.31 | 48.95 | 47.81 |
| 4 | | 0.328 | 0.781 | 0.0129 | 19 | | 4.81 | 4.52 | 9.28 |
| 5 | | 14.85 | 15.49 | | 20 | | 16.21 | 16.18 | 21.23 |
| 6 | | 12.31 | 0.0352 | 10.82 | 21 | | 121 | 0.324 | 1.25 |
| 7 | | 12.45 | 11.98 | | 22 | | 25.18 | 24.98 | |
| 8 | | 3.456 | 0.642 | 7.12 | 23 | | 3.1415 | 3.1411 | 10.91 |
| 9 | | 1.245 | 0.121 | 2.34 | 24 | | 3.14 | 1.57 | 0.0921 |
| 10 | | 13.12 | 0.145 | 15.18 | 25 | | 14.85 | 15.49 | |
| 11 | | 0.643 | 2.17 | 5.843 | 26 | | 5.325 | 5.152 | 5.481 |
| 12 | | 0.3575 | 2.63 | 0.854 | 27 | | 71.4 | 4.82 | 49.5 |
| 13 | | 14.91 | 0.485 | 14.18 | 28 | | 4.356 | 4.32 | 0.246 |
| 14 | | 16.5 | 4.12 | 0.198 | 29 | | 3.42 | 5.124 | 0.221 |
| 15 | | 5.21 | 14.9 | 0.295 | 30 | | 0.5761 | 3.622 | 0.0685 |