Файл: Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 151
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. ЦЕЛЬ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
2.1 Лабораторная работа 1. «Теория погрешностей и машинная арифметика»
2.2 Лабораторная работа 2. « Решение нелинейных уравнений»
2) Расчетные формулы методов решения нелинейного уравнения .
2.3 Лабораторная работа 3. « Интерполирование функций»
2.6 Лабораторная работа 6. «Методы численного интегрирования функций»
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт приоритетных технологий
Кафедра информационной безопасности
Н. А. Головачева
МЕТОДЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ ДЛЯ РЕШЕНИЯ ЗАДАЧ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ
учебно-методическое пособие для выполнения лабораторных работ
Волгоград, 2019
УДК 519.6(075.8)
ББК В19я7
Печатается по решению редакционно-издательского совета Волгоградского государственного университета
Рекомендовано в качестве учебно-методического пособия институтом приоритетных технологий
Волгоградского государственного университета
Рецензенты:
Профессор кафедры
САПР и ПК, д.т.н. Садовникова Н.П.
Профессор кафедры
ИБ ВолГУ, д.т.н. Афанасьев А.М.
Головачева Н. А.
Методы вычислительной математики для решения задач информационной безопасности [Текст] : учеб.-метод. пособие / Н. А. Головачева : Федер. гос. авт. образоват. учреждение высш. образования «Волгогр. гос. ун-т», Ин-т приоритет. технологий, Каф. информ. безопасности. – Волгоград: Изд-во ВолГУ, 2019. – 63с.
Пособие содержит 7 лабораторных работ. В нем раскрыты и обобщены теоретические вопросы и практические задания по темам дисциплины. Изложенный в учебно-методическом пособии материал соответствует требованиям ФГОС ВО.
Учебно-методическое пособие предназначено для студентов, обучающихся по укрупненной группе специальностей и направлений подготовки высшего образования 10.00.00 "Информационная безопасность" и может быть рекомендовано для дисциплин «Вычислительная математика», «Численные методы» и др.
УДК 519.6(075.8)
ББК В19я7
© Головачева Н. А.., 2019
© ФГАОУ ВО «Волгоградский
государственный университет», 2019
Содержание
1. ЦЕЛЬ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ 4
2. ЛАБОРАТОРНЫЕ РАБОТЫ 5
2.1 Лабораторная работа 1. «Теория погрешностей и машинная арифметика» 5
Таблица к задаче 2 13
2.2 Лабораторная работа 2. « Решение нелинейных уравнений» 13
2) Расчетные формулы методов решения нелинейного уравнения . 14
Таблица к задаче 2.2 Таблица к задаче 2.3 21
2.3 Лабораторная работа 3. « Интерполирование функций» 22
2.4 Лабораторная работа 4.« Решение систем линейных уравнений» 31
2.6 Лабораторная работа 6. «Методы численного интегрирования функций» 47
Рекомендуемая литература 63
1. ЦЕЛЬ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
Целью освоения дисциплины «Вычислительная математика» является формирование у студентов достаточных теоретических знаний и практических навыков по использованию методов вычислительной математики в профессиональной деятельности, в том числе, при их программной реализации на компьютерах.
Задачи дисциплины:
- изучение студентами методов расчета, методов оценки погрешностей и методов проведения машинного эксперимента;
- выработать у студентов умение применять соответствующие методы вычислительной математики для решения задач, в том числе профессиональных;
- овладение навыками решения задач в области информационной безопасности.
Отчетность
Отчет о выполнении лабораторных работ представляется в письменном виде. Отметка о сдаче лабораторной работы оформляется в виде таблицы:
| Отметка о выполнении лабораторной работы «№___» Тема: | ||||||
| Теоретическая часть | Практическая часть | |||||
| Дата | Отметка о выполнении | Подпись преподавателя | Дата | Отметка о выполнении | Подпись преподавателя | |
| | | | | | | |
Отчет по лабораторной работе должен содержать следующие материалы по каждой задаче:
1) постановка задачи;
2) необходимый теоретический материал;
3) ответы на контрольные вопросы;
4) результаты вычислительного эксперимента;
5) анализ полученных результатов и выводы;
6) графический материал (если необходимо);
7) тексты программ.
2. ЛАБОРАТОРНЫЕ РАБОТЫ
2.1 Лабораторная работа 1. «Теория погрешностей и машинная арифметика»
Цель: сформировать навыки решения задач на вычислительные погрешности.
Порядок выполнения работы
-
Теоретическая часть-
Основные определения
-
-
Абсолютная и относительная погрешность
Определение. Приближенным числом называется число, незначительно отличающееся от точного числа и заменяющее последнее в вычислениях.
Математическая запись
Определение. Под абсолютной погрешностью Δ приближенного числа понимается разность
Отсюда следует, что заключено в пределах
или
Определение. Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к модулю соответствующего точного числа
Так как обычно неизвестно, то на практике применяют оценку
2) Верные цифры числа
Всякое положительное число может быть представлено в виде конечной или бесконечной десятичной дроби
где - цифра числа в i – м разряде, m – старший десятичный разряд числа.
Пример:
Определение. Значащей цифрой приближенного числа называется всякая цифра в его десятичном представлении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда.
Пример. = 0.002080. Здесь только первые три нуля не являются значащими.
Определение. n первых значащих цифр приближенного числа являются верными, если абсолютная погрешность этого числа не превышает половины разряда, выражаемого n – й значащей цифрой, считая слева направо. Цифры, не являющиеся верными, называются сомнительными
Пример. Если в числе = 0.03450 все цифры верные, то .
Таким образом, если для приближенного числа известно, что
то, по определению, первые n цифр этого числа являются верными.
Пример. , . Тогда
Т.е. m-n+1=-1. Т.к. m = 1, то n = 3. Следовательно, приближенное число имеет 3 верных цифры и его следует округлить следующим образом:
3) Связь относительной погрешности с количеством верных знаков числа
Если положительное приближенное число имеет относительную погрешность, то количество верных знаков n данного числа можно определить по формуле
и в качестве n взять ближайшее целое к число.
4) Погрешности арифметических действий
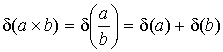
Общая формула вычисления погрешности
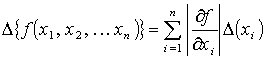
-
Машинный нуль, машинная бесконечность, машинный эпсилон.
В ЭВМ для вещественных чисел используется двоичная система счисления и принята форма представления чисел с плавающей точкой
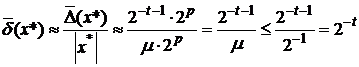 .
.Машинное эпсилон определяется разрядностью мантиссы и способом округления чисел, реализованным на конкретной ЭВМ.
Примем следующие способы определения приближенных значений параметров, требуемых в задаче:
1. Положим
2. Положим
3. Положим
Результаты вычислительного эксперимента:
Машинная бесконечность
машинный нуль
-
Контрольный пример
Задача 1. Постановка задачи: дан ряд