Файл: Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 156
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. ЦЕЛЬ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
2.1 Лабораторная работа 1. «Теория погрешностей и машинная арифметика»
2.2 Лабораторная работа 2. « Решение нелинейных уравнений»
2) Расчетные формулы методов решения нелинейного уравнения .
2.3 Лабораторная работа 3. « Интерполирование функций»
2.6 Лабораторная работа 6. «Методы численного интегрирования функций»
на N равностоящих узлов.
где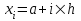 , шаг
, шаг 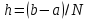 и обозначим
и обозначим 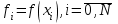
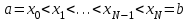
Выберем на каждом сегменте серединную точку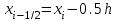 и обозначим
и обозначим 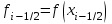
Квадратурная формула прямоугольников имеет вид:
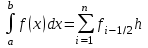
Если функции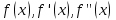 непрерывны на отрезке
непрерывны на отрезке  , то остаточный член имеет вид:
, то остаточный член имеет вид:
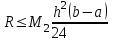 , где
, где 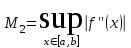
1.1.2. Квадратурная формула трапеций имеет вид:
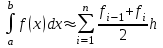
или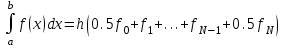
Если функции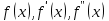 непрерывны на
непрерывны на  , то остаточный член представляется в виде:
, то остаточный член представляется в виде: 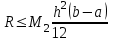 , где
, где 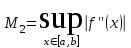
1.1.3. Квадратурная формула Симпсона
Выберем на каждом сегменте серединную точку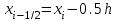 и обозначим
и обозначим 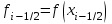
Квадратурная формула Симпсона: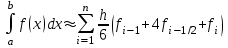
Также можно взять удвоенный частичный отрезок, обозначив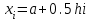 ,
, 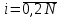 и
и 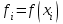 .
.
В результате получим другой вариант формулы Симпсона:
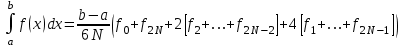
При этом, если функция имеет на отрезке
имеет на отрезке  непрерывные производные до четвертого порядка включительно, то остаточный член имеет вид:
непрерывные производные до четвертого порядка включительно, то остаточный член имеет вид:
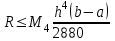 , где
, где 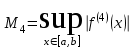
Решая неравенство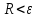 относительно h для остаточных членов любой из квадратурных формул и делая вычисления с таким шагом, получаем заданную точность
относительно h для остаточных членов любой из квадратурных формул и делая вычисления с таким шагом, получаем заданную точность 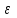 вычисления.
вычисления.
Пример 1. Вычислить интеграл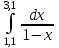 по квадратурным формулам прямоугольников, трапеций и Симпсона, сравнить с точным значением интеграла и вычислить остаточный член для каждой формулы.
по квадратурным формулам прямоугольников, трапеций и Симпсона, сравнить с точным значением интеграла и вычислить остаточный член для каждой формулы.
Решение: точное значение интеграла:
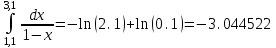
Для вычисления интеграла введем сетку, разделяющую отрезок на n=10 частей, при этом h=0,2. Выберем на каждом сегменте
на n=10 частей, при этом h=0,2. Выберем на каждом сегменте 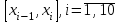 срединную точку
срединную точку 
Применяя квадратурную формулу прямоугольников получаем:
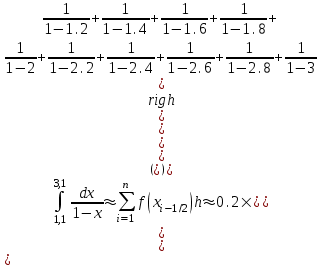
Оценим погрешность по общей формуле.
Поскольку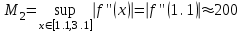 ,
,
то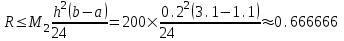
При сравнении точного значения интеграла и полученного имеем разницу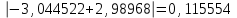 . Сравнивая эту разницу с погрешностью, можно сказать, что оценка явно завышена.
. Сравнивая эту разницу с погрешностью, можно сказать, что оценка явно завышена.
Введем сетку также, как в пункте 1.
При этом h=0.2, N=10 по квадратурной формуле трапеции:
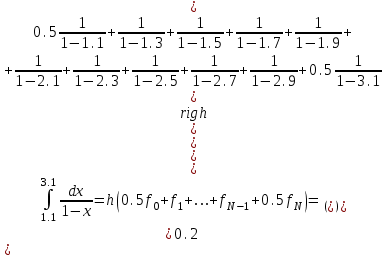
При этом оценка погрешности составляет:
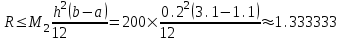
При сравнении точного и полученного значения интеграла разность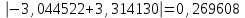 значительно меньше погрешности 0,66666 , что говорит о явно завышенной оценке.
значительно меньше погрешности 0,66666 , что говорит о явно завышенной оценке.
Введем сетку как в пункте 1. Пусть h=0.2, n=10.
Чтобы не использовать дробные индексы, обозначим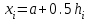 ,
, 
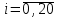 и записываем формулу Симпсона в виде:
и записываем формулу Симпсона в виде:
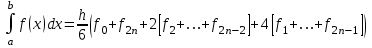
Вычислим интеграл по квадратурной формуле Симпсона:
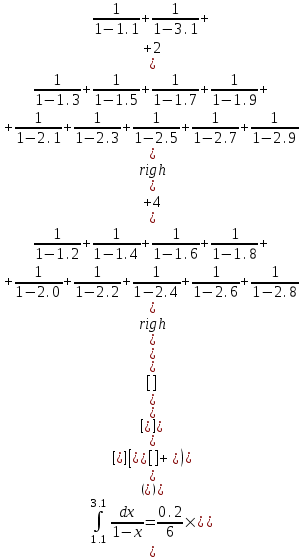
Оценка погрешности этой формулы:
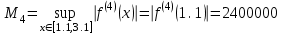
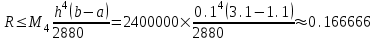
Сравнение точного значения интеграла с полученным дает разность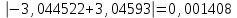 . Эта разность меньше погрешности. Можно сказать, что в данном случае оценка также завышена.
. Эта разность меньше погрешности. Можно сказать, что в данном случае оценка также завышена.
Пример 2. Выбрать шаг интегрирования для вычисления интеграла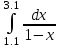 с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона. Оценку погрешности для каждой квадратурной формулы будем брать из примера 1 соответственно.
с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона. Оценку погрешности для каждой квадратурной формулы будем брать из примера 1 соответственно.
1. Квадратурная формула прямоугольников.
Вычислим, при каком шаге h погрешность будет составлять 0,01:
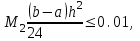
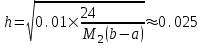
При шаге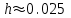 отрезок
отрезок 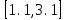 разбивается на N=80 равностоящих узлов.
разбивается на N=80 равностоящих узлов.
2. Квадратурная формула трапеций.
Вычислим, при каком шаге h погрешность составит 0,01:
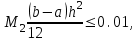
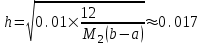
При шаге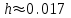
,отрезок разбивается на N=118 равностоящих узлов.
разбивается на N=118 равностоящих узлов.
3. Квадратурная формула Симпсона.
Вычислим, при каком шаге h погрешность составит 0,01:
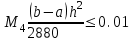
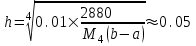
При шаге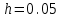 , отрезок
, отрезок  разбивается на N=40 равностоящих узлов.
разбивается на N=40 равностоящих узлов.
Как и следовало ожидать, наименьшее количество равностоящих узлов N=40 получается при вычислении интеграла по квадратурной формуле Симпсона.
4. Апостериорная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
Пусть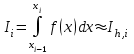 - квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть
- квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть 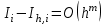 . Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке
. Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке 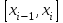 все вычисления дважды, один раз с шагом
все вычисления дважды, один раз с шагом 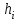 , другой раз с шагом
, другой раз с шагом 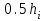 . Тогда справедлива оценка:
. Тогда справедлива оценка:
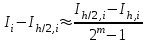
Если для заданного правая часть не превосходит
правая часть не превосходит 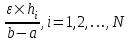 , то получим:
, то получим: 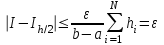 ,то есть будет достигнута заданная точность
,то есть будет достигнута заданная точность  .
.
Если же на каком-то из частичных отрезков эта оценка не будет выполняться, то шаг на этом отрезке надо измельчить еще в два раза и снова оценить погрешность. Заметим, что для некоторых функций такое измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений, а также возможность увеличения
.
2. Контрольные вопросы
3. Практические задания
Вычислить приближенное значение интеграла с помощью формулы а) прямоугольников, б) трапеций, в) Симпсона. Величину шага выбрать заранее, сделав вручную оценку погрешности через вторую (случаи а,б) или четвертую (случай в) производные. Сравнить с точным значением интеграла.
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 6.
1.(а)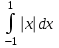 1.(б)
1.(б) 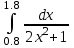 1.(в)
1.(в) 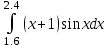
2.(а)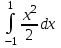 2.(б)
2.(б) 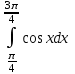 2.(в)
2.(в) 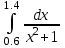
3.(а)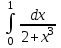 3.(б)
3.(б) 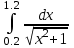 3.(в)
3.(в) 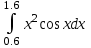
4.(а)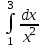 4.(б)
4.(б) 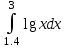 4.(в)
4.(в) 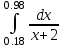
5.(а)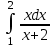 5.(б)
5.(б) 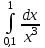 5.(в)
5.(в) 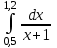
6.(а)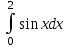 6.(б)
6.(б) 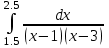 6.(в)
6.(в) 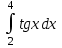
7.(а)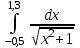 7.(б)
7.(б) 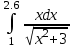 7.(в)
7.(в) 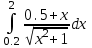
8.(а)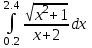
где
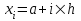 , шаг
, шаг 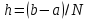 и обозначим
и обозначим 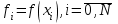
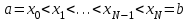
Выберем на каждом сегменте серединную точку
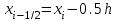 и обозначим
и обозначим 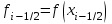
Квадратурная формула прямоугольников имеет вид:
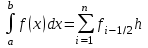
Если функции
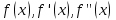 непрерывны на отрезке
непрерывны на отрезке  , то остаточный член имеет вид:
, то остаточный член имеет вид: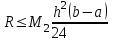 , где
, где 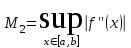
1.1.2. Квадратурная формула трапеций имеет вид:
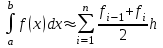
или
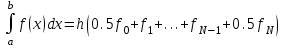
Если функции
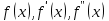 непрерывны на
непрерывны на  , то остаточный член представляется в виде:
, то остаточный член представляется в виде: 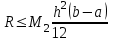 , где
, где 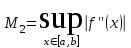
1.1.3. Квадратурная формула Симпсона
Выберем на каждом сегменте серединную точку
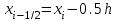 и обозначим
и обозначим 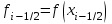
Квадратурная формула Симпсона:
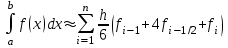
Также можно взять удвоенный частичный отрезок, обозначив
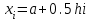 ,
, 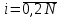 и
и 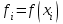 .
.В результате получим другой вариант формулы Симпсона:
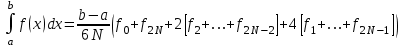
При этом, если функция
 имеет на отрезке
имеет на отрезке  непрерывные производные до четвертого порядка включительно, то остаточный член имеет вид:
непрерывные производные до четвертого порядка включительно, то остаточный член имеет вид: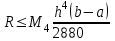 , где
, где 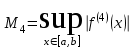
Решая неравенство
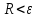 относительно h для остаточных членов любой из квадратурных формул и делая вычисления с таким шагом, получаем заданную точность
относительно h для остаточных членов любой из квадратурных формул и делая вычисления с таким шагом, получаем заданную точность 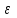 вычисления.
вычисления.-
Контрольный пример
Пример 1. Вычислить интеграл
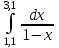 по квадратурным формулам прямоугольников, трапеций и Симпсона, сравнить с точным значением интеграла и вычислить остаточный член для каждой формулы.
по квадратурным формулам прямоугольников, трапеций и Симпсона, сравнить с точным значением интеграла и вычислить остаточный член для каждой формулы.Решение: точное значение интеграла:
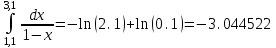
-
Квадратурная формула прямоугольников
Для вычисления интеграла введем сетку, разделяющую отрезок
 на n=10 частей, при этом h=0,2. Выберем на каждом сегменте
на n=10 частей, при этом h=0,2. Выберем на каждом сегменте 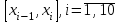 срединную точку
срединную точку 
Применяя квадратурную формулу прямоугольников получаем:
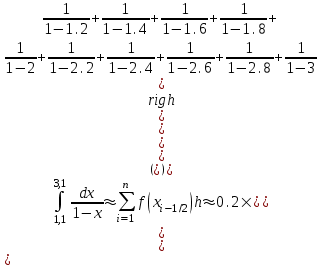
Оценим погрешность по общей формуле.
Поскольку
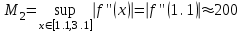 ,
, то
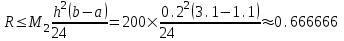
При сравнении точного значения интеграла и полученного имеем разницу
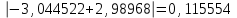 . Сравнивая эту разницу с погрешностью, можно сказать, что оценка явно завышена.
. Сравнивая эту разницу с погрешностью, можно сказать, что оценка явно завышена.-
Квадратурная формула трапеций.
Введем сетку также, как в пункте 1.
При этом h=0.2, N=10 по квадратурной формуле трапеции:
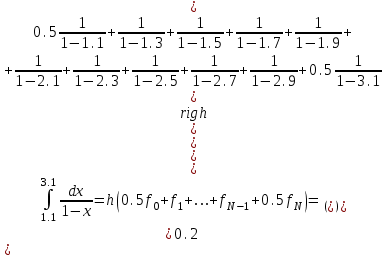
При этом оценка погрешности составляет:
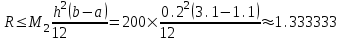
При сравнении точного и полученного значения интеграла разность
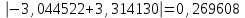 значительно меньше погрешности 0,66666 , что говорит о явно завышенной оценке.
значительно меньше погрешности 0,66666 , что говорит о явно завышенной оценке.-
Квадратурная формула Симпсона.
Введем сетку как в пункте 1. Пусть h=0.2, n=10.
Чтобы не использовать дробные индексы, обозначим
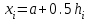 ,
, 
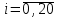 и записываем формулу Симпсона в виде:
и записываем формулу Симпсона в виде: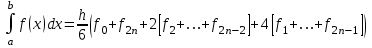
Вычислим интеграл по квадратурной формуле Симпсона:
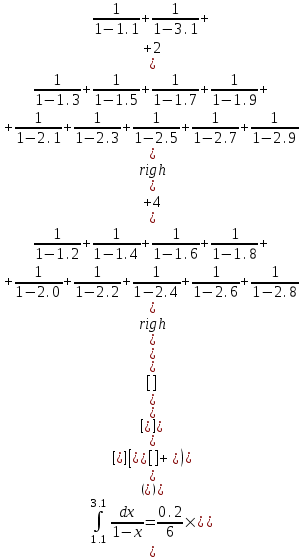
Оценка погрешности этой формулы:
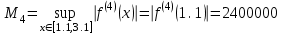
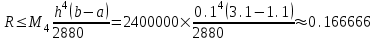
Сравнение точного значения интеграла с полученным дает разность
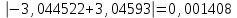 . Эта разность меньше погрешности. Можно сказать, что в данном случае оценка также завышена.
. Эта разность меньше погрешности. Можно сказать, что в данном случае оценка также завышена.Пример 2. Выбрать шаг интегрирования для вычисления интеграла
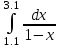 с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона. Оценку погрешности для каждой квадратурной формулы будем брать из примера 1 соответственно.
с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона. Оценку погрешности для каждой квадратурной формулы будем брать из примера 1 соответственно.1. Квадратурная формула прямоугольников.
Вычислим, при каком шаге h погрешность будет составлять 0,01:
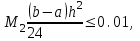
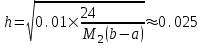
При шаге
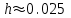 отрезок
отрезок 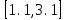 разбивается на N=80 равностоящих узлов.
разбивается на N=80 равностоящих узлов.2. Квадратурная формула трапеций.
Вычислим, при каком шаге h погрешность составит 0,01:
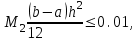
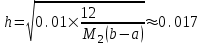
При шаге
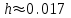
,отрезок
 разбивается на N=118 равностоящих узлов.
разбивается на N=118 равностоящих узлов.3. Квадратурная формула Симпсона.
Вычислим, при каком шаге h погрешность составит 0,01:
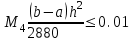
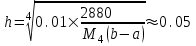
При шаге
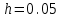 , отрезок
, отрезок  разбивается на N=40 равностоящих узлов.
разбивается на N=40 равностоящих узлов.Как и следовало ожидать, наименьшее количество равностоящих узлов N=40 получается при вычислении интеграла по квадратурной формуле Симпсона.
4. Апостериорная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
Пусть
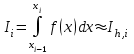 - квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть
- квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть 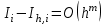 . Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке
. Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке 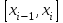 все вычисления дважды, один раз с шагом
все вычисления дважды, один раз с шагом 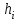 , другой раз с шагом
, другой раз с шагом 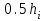 . Тогда справедлива оценка:
. Тогда справедлива оценка: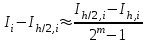
Если для заданного
 правая часть не превосходит
правая часть не превосходит 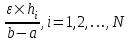 , то получим:
, то получим: 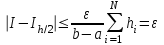 ,то есть будет достигнута заданная точность
,то есть будет достигнута заданная точность  .
.Если же на каком-то из частичных отрезков эта оценка не будет выполняться, то шаг на этом отрезке надо измельчить еще в два раза и снова оценить погрешность. Заметим, что для некоторых функций такое измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений, а также возможность увеличения

.
2. Контрольные вопросы
-
Какая формула называется квадратурной и почему? -
Запишите остаток квадратурной формулы. -
В каком случае применяются квадратурные формулы с равностоящими узлами? -
Запишите и поясните квадратурную формулу прямоугольников. -
Запишите и поясните квадратурную формулу трапеций. -
Запишите и поясните квадратурную формулу Симпсона. -
Как получается заданная точность вычисления?
3. Практические задания
Вычислить приближенное значение интеграла с помощью формулы а) прямоугольников, б) трапеций, в) Симпсона. Величину шага выбрать заранее, сделав вручную оценку погрешности через вторую (случаи а,б) или четвертую (случай в) производные. Сравнить с точным значением интеграла.
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 6.
1.(а)
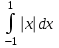 1.(б)
1.(б) 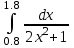 1.(в)
1.(в) 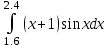
2.(а)
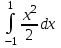 2.(б)
2.(б) 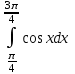 2.(в)
2.(в) 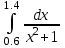
3.(а)
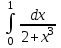 3.(б)
3.(б) 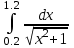 3.(в)
3.(в) 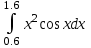
4.(а)
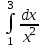 4.(б)
4.(б) 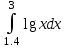 4.(в)
4.(в) 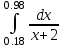
5.(а)
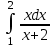 5.(б)
5.(б) 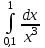 5.(в)
5.(в) 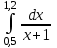
6.(а)
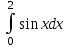 6.(б)
6.(б) 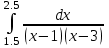 6.(в)
6.(в) 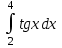
7.(а)
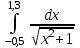 7.(б)
7.(б) 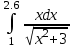 7.(в)
7.(в) 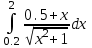
8.(а)