Файл: 3.doc

Різниця між числом невідомих зусиль, які підлягають визначенню, і числом невідомих рівнянь статики визначає степінь статичної невизначеності системи, тобто степінь статичної невизначеності рівна числу додаткових або “зайвих” зв’язків. Розрізняють один, два і т.д. раз статично невизначені системи.

Визначення всіх невідомих сил, або, як говорять, розкриття статичної невизначеності, можливе тільки шляхом складання рівнянь, які доповнюють число рівнянь статики до числа невідомих. Ці додаткові рівняння відображають особливості геометричних зв’язків, накладених на системи, які деформуються, і умовно називаються рівняннями переміщень або рівняннями деформацій.

Розв’язок статично невизначених задач проводять в наступні послідовності:

1. Відкидаємо зв’язки і заміняємо їх реакціями, скориставшись при цьому методом перерізів.

2. Складаємо всі можливі незалежні рівняння статики для відсічених елементів системи, які містять невідомі зусилля. Визначаємо ступінь статичної невизначеності системи.

3. Розглядаючи систему в деформованому стані, встановлюємо зв’язки між деформаціями або переміщеннями окремих елементів конструкції і складаємо рівняння сумісності переміщень.

4. В рівняннях сумісності переміщень деформації елементів виражають на основі закону Гука через діючі в них невідомі зусилля.

5. Розв’язують спільно отриману систему рівнянь, яка складається з рівнянь статики і рівнянь сумісності переміщень, відносно невідомих зусиль.

Приклад

Для заданої системи визначити діаметр стержнів якщо відоме відношення їх площ і величина діючого навантаження.

Дано: а=1м; =60⁰; F=12т; А₁=2А₂; Е₁=Е₂=Е; матеріал сталь 3; []=160МПа=1600кг/см² (додаток 3).

В задачі необхідно визначити діаметр стержнів, тобто виконати проектний розрахунок. Так як стержні системи зазнають деформації розтягу-стиску, то проектний розрахунок виконується по формулі

.

Допустиме напруження нам задано, тому для відповіді на питання задачі необхідно визначити нормальні сили в поперечних перерізах стержнів 1 і 2.

Скористаємося методом перерізів і розсічемо підвіски поперечними перерізами, відкинувши верхню частину стержня 1 і нижню частину стержня 2 та замінимо їх дію нормальними силами N₁ і N₂ (рис.4.1,б). Але тепер виникає питання – як направити N₁ і N₂? Тобто який із стержней стиснутий, а який – розтягнутий? Для простих систем, подібних тій яку ми розглядаємо, відповідь на це питання достатньо очевидна. Однак, для більш складних стержневих систем відповісти на нього не так просто. Тому в більшості випадків зручно використовувати формальний підхід.

Використовуючи формальний підхід, припустимо, що стержень 1 розтягнутий, стержень 2 стиснутий, тобто направимо N₁ від перерізу, а N₂ до перерізу. Відкинемо також в’язі, накладені на балку в шарнірі і замінимо їх реакціями R_x і R_y.

Для визначення чотирьох невідомих N₁, N₂, R_x, R_y ми можемо скласти лише 3 незалежних рівняння статики, тобто X=0; Y=0; M₀=0. Таким чином, система 1 раз статично невизначена.

Перші два рівняння статики крім N₁ і N₂ містять невідомі реакції R_x і R_y, визначати які нема необхідності. Таким чином, відносно зусиль які нас цікавлять N₁ і N₂ ми маємо лише одне рівняння:

M₀=F(2a+1.5a)-N₁(a+2a+1.5a)sin60⁰-N₂1.5a=0. (4.1)

a)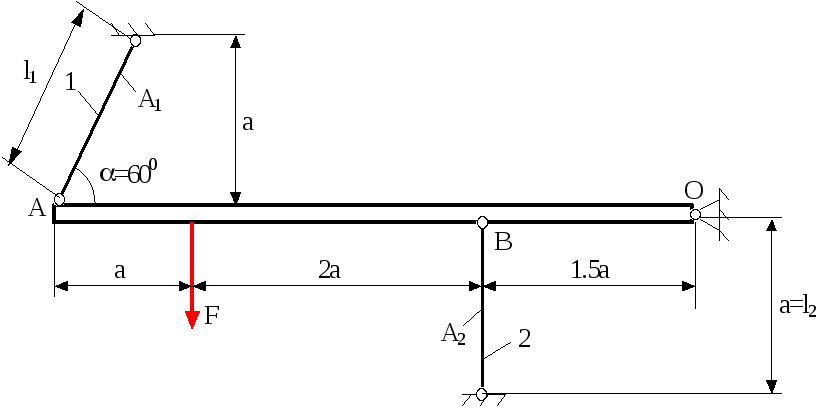

б)

в)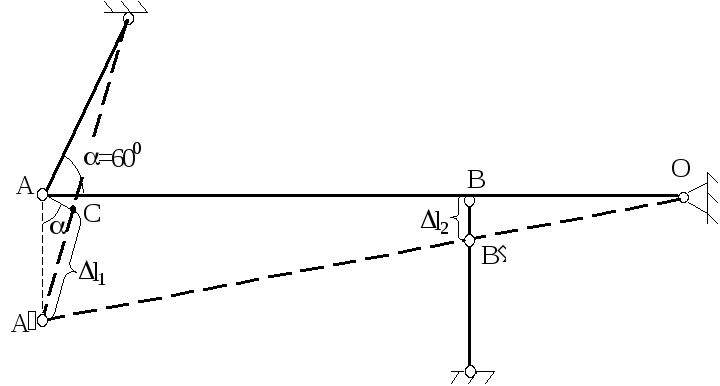

Рис.4.1

Для визначення N₁ і N₂ необхідно скласти одне рівняння спільності переміщень. З цією метою розглянемо систему в деформованому стані.

З подібності ОВВ і ОАА находимо

.

АА=3ВВ (4.2)

Із ААС .

З урахуванням цього (4.2) приймає вид

; . (4.3)

Це рівняння сумісності переміщень.

Виразимо l₁ і l₂ через зусилля в стержнях N₁ і N₂

;.

Приймаючи до уваги, що А₁=2А₂, ,,l₂=a підставимо вирази для l₁ і l₂ в рівняння (4.2).

,

. (4.4)

Сумісним розв’язком рівнянь (4.1) і (4.4) визначимо N₁ і N₂

F(2a+1.5a)-4.5N₂(a+2a+1.5a)sin60⁰-N₂1.5a=0,

F(2a+1.5a)-N₂[4.5(a+2a+1.5a)sin60⁰+1.5a]=0,

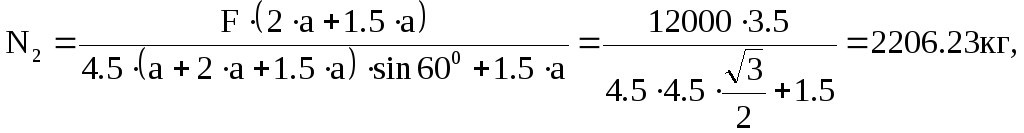
N₁=4.5N₂=4.52206.23=9928.03кг.

Отримані позитивні знаки зусиль говорять про те, що при навантаженні системи силою F стержень 1 зазнає розтягу, і стержень 2 – стиску.

Порівняння величин N₁ і N₂ показує, що перший стержень є більш навантаженим. Визначимо необхідну площу А₁.

;

Приймаємо d₁=2.8см. Тоді

Напруження в стержні 1

Перенапруження

Тому можна прийняти d₁=2.8см.

Перевіримо міцність 2-го стержня

,

[]=1600кг/см².

Умова міцності – виконується.

.

Приймаємо d₂=2см.

5. Геометричні характеристики поперечних перерізів бруса.

При розтягу стиску брусів було встановлено, що видовження поперечних перерізів брусів l залежить від жорсткості перерізів брусів ЕА, де Е – модуль пружності матеріалу, А – площа поперечного перерізу бруса (рис.5.1).

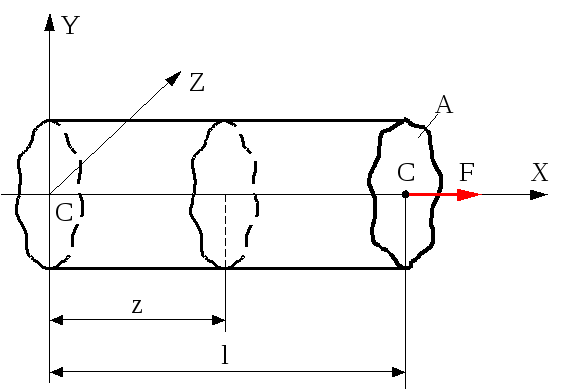
Рис.5.1

В цьому випадку розтягуюча або стискаюча сила повинна бути прикладена в центрі ваги поперечного перерізу А.

По схемі рис.5.1 ось X розташована вздовж лінії центрів ваги поперечних перерізів, а центральні осі Z і Y по відношенню до контуру перерізу А можуть займати довільні положення.

Очевидно, що декілька брусів, виконаних з одного і того ж матеріалу і які мають рівновеликі площі А але різні геометрії перерізу, при розтягу і стиску силою F отримують однакові видовження

(5.1)

у відповідних поперечних перерізах z (0zl).

При підрахуванні величини (5.1) форма перерізу А і її орієнтація по відношенню до центральних осей Z і Y не грали ніякої ролі.

Якщо ж силу F паралельно перенести в другу точку з деякими координатами z₀, y₀, то ті ж самі бруси з рівновеликими площами А будуть чинити різний опір дії сили F.

Та ж сила F (рис.5.2) буде здійснювати різні згини бруса, будучи прикладеною в площині ZOX, або в площині YOX або в будь які іншій площині, нахиленій під кутом  до центральних осей Z і Y.

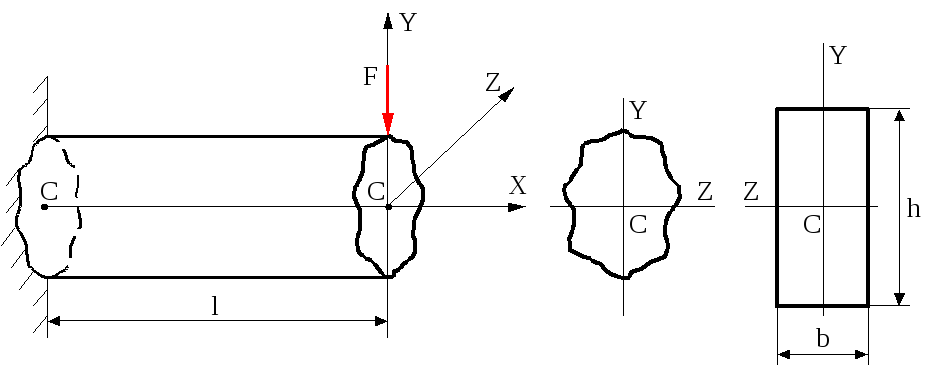
Рис.5.2

Для практичних цілей бажано заздалегідь передбачити варіанти найкращого і найгіршого опору бруса дії згинаючого моменту.

В балці прямокутного перерізу (hb) такими варіантами по схемі рис.5.2 є випадки, коли сила F почергово прикладається в площинах YOX і ZOX. В цьому випадку координатні осі Z і Y співпадають з осями симетрії прямокутного поперечного перерізу.

Визначення координат центра ваги плоскої фігури.

Відомо, що центр ваги плоскої фігури А, що має дві і більше осей симетрії, лежить на перетині осей симетрії.

Фігура А несиметричної форми розглядається в довільній системі координат Z і Y (рис.5.3) і ця система відліку може розташовуватися як в межах площі А, а так і за її межами.

Площі найпростіших фігур підраховуються по відомим формулам геометрії, а площі складних фігур визначаються шляхом інтегрування

. (5.2)

Координати центра ваги площі будь-якої конфігурації підраховуються по формулам:

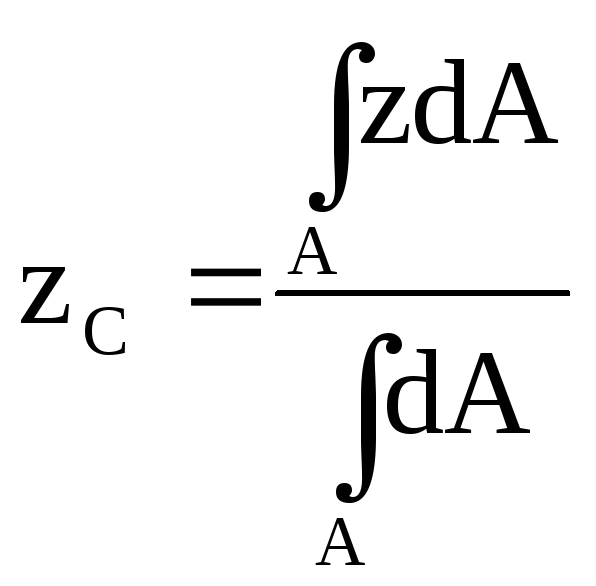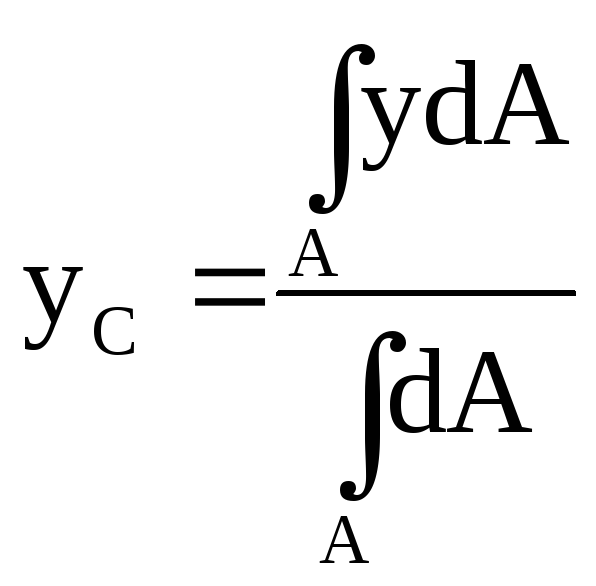, . (5.3)

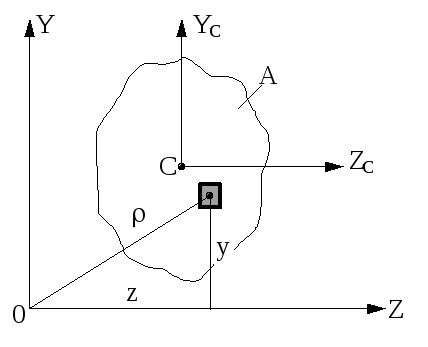
Рис.5.3

Чисельники рівнянь (5.3) називаються статичними моментами площі А відносно осей z і y і позначаються так:

, . (5.4)

Таким чином, формули для визначення координат центра ваги (5.3) за допомогою виразів (5.2) і (5.4) приводяться до простих рівнянь:

, , (5.5)

в яких площа А завжди є додатною величиною, а статичні моменти площі в залежності від розташування осей Z і Y по відношенню до контуру площі можуть бути як додатними, так і від’ємними величинами.

В випадку S_z=0 і S_y=0 допоміжні осі Z і Y проходять через центр ваги перерізу.

Для складних перерізів, які можна розбити на ряд простих (прямокутники, трикутники, круг і т.д.) статичні моменти (5.4) зручніше підраховувати по формулам:

S_z=А₁y_C1+А₂y_C2+…+А_ny_Cn,