Файл: 3.doc

(5.6)

S_y=А₁z_C1+А₂z_C2+…+А_nz_Cn,

де А₁, А₂ ... А_n – площі простих фігур, z_C1, y_C1, z_C2, y_C2 ... z_Cn, y_Cn – координати центра ваги цих фігур відносно вибраних осей Z і Y. Осі Z і Y намагаються назначати таким чином, щоб спрощувались математичні підрахунки по записам (5.6).

Моменти інерції перерізу

Осьові моменти інерції перерізу А відносно осей Z і Y і відцентровий момент інерції відносно тих же осей (рис.5.4) підраховується за допомогою інтегралів:

, ,. (5.7)

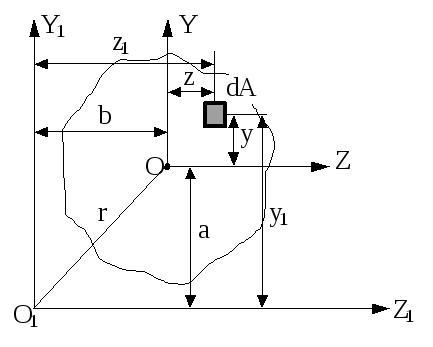
Рис.5.4

Полярний момент інерції перерізу А відносно точки перетину осей Z і Y визначається виразами:

. (5.8)

При розв’язку конкретних задач по теорії згину і кручення стержней частіше всього вирази (5.7) і (5.8) підраховуються відносно деяких центральних осей і точки їх перетину.

В складних перерізах, аналогічних розглянутим вище прикладам, підрахунок величин (5.7) і (5.8) значно спрощується за допомогою теореми про паралельний перенос осей:

I_z1=I_z+2aS_z+a²A,

I_y1=I_y+2bS_y+b²A,

I_z1y1=I_zy+bS_z+aS_y+abA.

Якщо осі z і y центральні, то S_z=S_y=0 і приведені вище вирази спрощуються

I_z1=I_zC+a²A,

I_y1=I_yC+b²A, (5.9)

I_z1y1=I_zCyC+abA,

де а – відстань між паралельними осями Z і Z_С; b – відстань між паралельними осями Y і Y_С.

Зміна моментів інерції при повороті осей. Головні осі і головні моменти інерції

В розглянутих вище прикладах ми визначали моменти інерції відносно центральних осей, зображених “стандартним” чином в першому квадранті.

В залежності від кута повороту цих осей величини моментів інерцій будуть підраховуватися наступним чином:

,

,

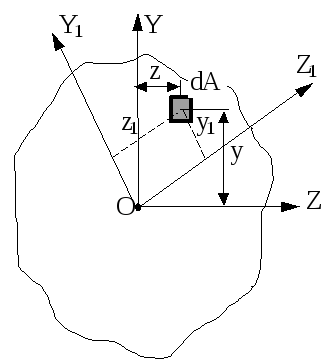
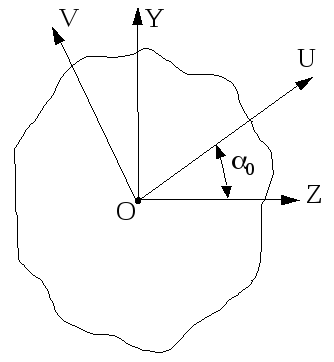
Рис.5.5

,

,

,

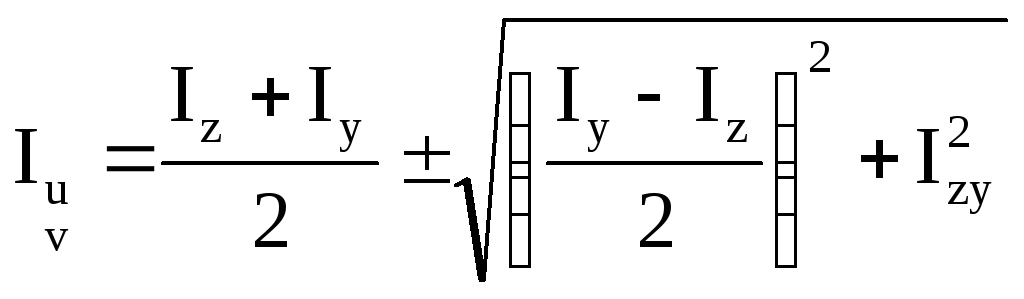де I_u – найбільший головний момент інерції,

I_v – найменший головний момент інерції.

Приклад

Для заданого перерізу (рис.5.6) визначити, користуючись таблицями сортаменту, аналітичним способом положення головних центральних осей і величину головних центральних моментів інерції.

Переріз складається з двутавра №30а і кутника 1409010, а=0.1b=0.1145=14.5мм.

Відповідно до ДЕСТ 8239-72 (додаток 6) для двутавра №30а: b=145мм, A₁=49.9см², I_Z1=7780см⁴, I_Y1=436см⁴.

Дані для кутника по сортаменту (додаток 7): A₂=22.2см², I_Z2=146см⁴, I_Y2=444см⁴, I_ZY=147см⁴.

Даний переріз креслиться в масштабі (рис.5.6). Центр ваги визначається в системі допоміжних осей. Відстані від осей Y і Z до центра ваги двутавра С₁

;

Відстані від цих осей до центра ваги кутника

y₂=300+21.2=321.2мм=32.12см; z₂=14.5+140-45.8=108.7мм=10.87см

Координати центра ваги перерізу С

;

Точка С наноситься на креслення. При правильному визначенні її положення точка С лежить на прямі С₁С₂, яка з’єднує центри ваги двутавра та кутника.

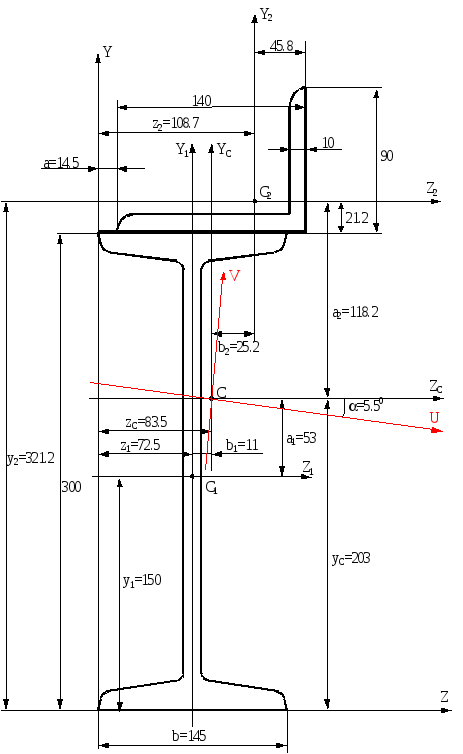
Рис.5.6

Користуючись формулами переходу до паралельних осей, визначимо моменти інерції перерізу відносно центральних осей Z_С і Y_C.

де а₁=y₁-y_C=15-20.3=-5.3см=-53мм,

а₂=y₂-y_С=32.12-20.3=11.82см=118.2мм,

b₁=z₁-z_C=7.25-8.35=-1.1см=-11мм,

b₂=z₂-z_C=10.87-8.35=2.52см=25,2мм.

Відцентровий момент інерції всього перерізу відносно осей Z_С і Y_C.

Якщо осьові моменти інерції мають тільки додатні значення, то центробіжні можуть бути як додатні, так і від’ємні.

Кут нахилу головних осей інерції до центральних осей.

; 2=-11⁰; =-5.5⁰

Головні моменти інерції перерізу.

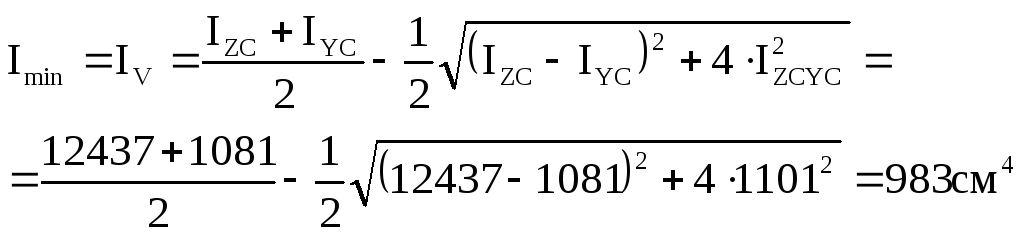
6. Розрахунок на міцність при згині

В загальному випадку при плоскому прямому згині в поперечному перерізі балки виникають два внутрішніх силових фактора – згинаючий момент і поперечна сила. У відповідності з цим в поперечному перерізі балки з’являються нормальні і дотичні напруження. Нормальне напруження розраховують по формулі:

,

де М_z – згинаючий момент в перерізі балки, який розглядається,

I_z – момент інерції перерізу відносно нейтральної осі Z,

y – координата точки, в які розраховується напруження, яка відраховується від осі Z.

Дотичні напруження визначають по формулі Д.І.Журавського:

,

де Q_y – поперечна сила в перерізі балки, який розглядається,

S_z – статичний момент відносно нейтральної осі Z відсіченої частини перерізу, яка розташована вище або нижче рівня, на якому визначається напруження,

b – ширина перерізу на рівні, який розглядається.

Розрахунок на міцність при згині ведуть в основному по нормальним напруженням, виходячи з умови міцності

,

де _max – найбільше нормальне напруження, яке виникає в точках найбільш віддалених від нейтральної лінії,

M_z – розрахункове значення згинаючого моменту, яке встановлюється з епюри,

 - допустиме напруження,

– осьовий момент опору (y_max – координата точки перерізу, найбільш віддаленої від нейтральної лінії).

В більшості випадків дотичні напруження невеликі і їх розрахунок не представляє практичного інтересу. Винятки можуть мати місце при розрахунку тонкостінних балок (наприклад зварних двотаврових), які навантажені великими зосередженими силами поблизу опор, або балок, які мають малу довжину, а також при розрахунку дерев’яних балок, які погано чинять опір зсуву вздовж волокон. У вказаних випадках, поряд з основним розрахунком по нормальним напруженням належить виконати розрахунок по найбільшим дотичним напруженням, які виникають в тому поперечному перерізі, де поперечна сила максимальна. Найбільші дотичні напруження для перерізів, які найбільш часто зустрічаються, типу круг, прямокутник, тавр, двутавр, швелер, кутник, трикутник, виникають на нейтральній осі. Умова міцності в цьому випадку має вид

,

де Q_y – розрахункове значення поперечної сили, яке визначається з епюри,

 – допустиме напруження на зсув,

b – ширина профілю на рівні нейтральної осі.

На міцність по нормальним напруженням при згині перевіряються крайні волокна перерізу, які зазнають розтягу або стиску.

На міцність по дотичним напруженням при поперечному згині розраховується елемент нейтрального шару, який знаходиться в умовах чистого зсуву.

Приклад

Для заданої балки (рис.6.1) підібрати двотавровий, круглий і прямокутний (h=2b) переріз і порівняти вагу одного метра довжини кожного профілю.

Виконати повну перевірку міцності двотаврової балки (по головним напруженням).

Матеріал балок: Ст.3.

[]=160МПа (додаток 3); []=0.6[]=100МПа; Е=210⁵МПа (додаток 4); а=1м; q=50кН/м; F=80кН; М=40кНм.

Будуємо епюри поперечних сил Q_y та згинаючих моментів M_z. Небезпечним по нормальних напруженнях буде переріз А.

Використовуючи умову міцності по нормальним напруженням підбирається переріз балки

,