Файл: УП по задачам.doc

По мнению М.И. Моро начать надо с задач в два действия, которые включают простые задачи на уменьшение числа на несколько единиц и на нахождение суммы. Она считает, что при решении такой составной арифметической задачи дети быстрее, чем в задачах ранее указанной структуры, увидят, что её нельзя решить одним действием, чтобы ответить на вопрос задачи.

На наш взгляд, выбор варианта существенного значения не имеет. Важно методически грамотно провести подготовительную ступень с учётом того варианта, который выбран.

Первыми вводятся составные арифметические задачи, включающих в себя простые задачи на увеличение числа на несколько единиц и на нахождение суммы..

Выберем вариант, предложенный авторами учебника математики 1 класса.

Например. На первой проволоке 7 шариков, а на второй – на 3 шарика больше, Сколько всего шариков на двух проволоках?

Рассмотрим ознакомление с составной арифметической задачей данной структуры.

Варианты работы учителя на этом этапе могут быть различными.

Один из них - предложить задачу в готовом виде и выполнить под руководством и с помощью учителя все операции деятельности по ее решению.

Учитель читает задачу: «На первой проволоке 7 шариков, а на второй – на 3 шарика больше. Сколько всего шариков на двух проволоках?».

Выясняется, что известно в задаче, что надо узнать. Затем выполняется краткая запись задачи.

I проволока – 7 ш.

? ш.

II проволока – ? ш., на 3 ш. б.

- Повторим вопрос задачи. Начнём выполнять «схему размышления», как это мы делали раньше. (Учитель выполняет на доске.)

- Посмотрите внимательно на краткую запись и подумайте, чтобы узнать, сколько всего шариков на двух проволоках, что для этого надо знать, посмотрите на краткую запись задачи? (Надо знать, сколько шариков на первой проволоке и сколько на второй.) Учитель продолжает выполнение «схемы».

- А если бы мы знали, сколько шариков на первой проволоке и сколько на второй, то каким действием смогли бы узнать, сколько шариков на двух проволоках вместе? (Действием сложения. Отметим это в «схеме».

- Подумайте, можем мы сразу узнать, сколько шариков на двух проволоках? (Нет.)

- Почему? (Не знаем, сколько шариков на второй проволоке.)

- Отмечаем это в «схеме». Ставим около слов «II проволока» вопросительный знак.

- Что теперь нам надо узнавать, посмотрите на «схему». Где появился ещё один вопросительный знак? (Надо узнавать, сколько шариков на второй проволоке?)

- Что нужно знать, чтобы узнать, сколько шариков на второй проволоке? (Надо знать, сколько шариков на первой проволоке и на сколько шариков больше на второй проволоке, чем на первой.) Учитель отмечает в «схеме».

- Это мы можем узнать сразу? (Да.)

- Каким действием? (Действием сложения.) Учитель ставит в «схеме» знак «+».

- Посмотрите на «схему», сколько раз мы выполняли действие, чтобы ответить на вопрос задачи: «Сколько шариков на двух проволоках?» (Два раза.)

- Вспомните, раньше для решения задач сколько действий выполняли? (Одно.)

- Значит, есть задачи, в которых нельзя сразу, выполнив одно действие, ответить на её вопрос.

- Действий в решении этой задачи два. Нужно установить, в каком порядке будем их выполнять, составим план решения.

- Что узнаем сначала?

- Каким действием? (Учитель отмечает в схеме: ставит «1» над знаком «+» в «схеме»).

• Что узнаем потом?

• Каким действием? (Поступает аналогично.)

Можно по ходу составления «схемы» над прямоугольниками писать числа, которые даны в задаче (когда «схема» будет выполняться самими детьми в тетрадях, числа, данные в задаче, постепенно записывать карандашом над прямоугольниками; это позволит при записи решения работать только со «схемой».).

С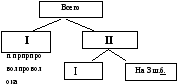хема приобретает вид:

?

2

+ ?

1

1

+

- Запишем решение задачи выражением с полным пояснением (выражение составляется по ступенькам).

7+3 (ш.) - столько на второй проволоке,

(7+3) +7 (ш.) - столько всего на двух проволоках,

(7+3) +7=17 (ш.).

Ответ: 17 шариков.

После решения задачи подводится итог: что нового узнали при решении этой задачи? (Задачу не всегда можно решить, выполнив действие один раз.)

Далее на этом и последующих уроках решаются аналогичные задачи с постепенным увеличением самостоятельности детей. Памятка может быть введена позднее. Методика её введения аналогична ознакомлению детей с памяткой по решению простой арифметической задачи (см. п.7).

Постепенно вводятся задачи другой математической структуры (см. выше). Работа над задачами строится в соответствии с общими положениями (см. п.6). Предлагаемые задачи должны быть с разной структурой текста (стандартной и нестандартной.)

В период ознакомления с составными задачами, как отмечает М.А. Бантова, очень важно добиться различения детьми простых и составных задач. С этой целью надо составные задачи перемежать с простыми арифметическими задачами, выясняя каждый раз, почему одна из них решается одним действием, а другая двумя; составные задачи преобразовывать в простые и обратно; включать задания на составление задач, аналогичных решённой; на составление задач по данному решению, по краткой записи; по «схеме размышления» и др.

В дальнейшем решаются составные арифметические задачи, которые органически связываются с изучаемым материалом. По мере продвижения учащихся задачи усложняются: либо по линии включения новых связей, т.е. новых видов простых задач, либо по линии увеличения числа арифметических действий (1 класс - задачи в два действия, 2,3 класс - преимущественно 2-3 действия, 4 класс - в 2-4 действия).

Наряду с нетиповыми составными арифметическими задачами постепенно вводятся типовые арифметические задачи с пропорциональными величинами. Методика работы над ними будет рассмотрена в следующем параграфе.

Необходимо отметить, что в новом учебнике сделана попытка дать план решения составной арифметической задачи. Однако выделенная система операций отличается от той системы операций, которая должна выполняться решающим задачу. Таким образом, с самого начала формируется деятельность по решению задачи, являющаяся дефектной. Это не может способствовать формированию полноценного умения решать составные арифметические задачи и обеспечить перенос сформированного умения на задачи новой математической структуры.

§ 9. Методика формирования умения решать составные арифметические задачи, связанные с пропорциональными величинами

План

1. Методика формирования умения решать задачи на нахождение четвёртого пропорционального.

2. Методика формирования умения решать задачи на пропорциональное деление.

3. Методика формирования умения решать задачи на нахождение неизвестных по двум разностям.

4. Методика работы над задачами на движение.

В начальных классах рассматривается решение задач, связанных с пропорциональными величинами: задачи на нахождение четвёртого пропорционального, на пропорциональное деление, на нахождение неизвестного по двум разностям. Кроме этого, специально рассматриваются задачи, связанные с движением.

Решение этих задач основывается на знании связей между соответствующими величинами.

9.1. Задачи на нахождение четвёртого пропорционального

В задачах этого типа даны три величины, связанные прямо или обратно пропорциональной зависимостью, из них две переменные и одна постоянная, при этом даны два значения одной переменной и одно из соответствующих значений другой переменной, а второе значение этой величины является искомым.

Для любых трёх величин, связанных пропорциональной зависимостью, можно составить шесть видов задач на нахождение четвёртого пропорционального.

Рассмотрим на примере задач с величинами цена, количество, стоимость [1].

В таблице дана классификация задач на нахождение четвёртого пропорционального с величинами цена, количество, стоимость.

Как видно из таблицы, первые четыре задачи с прямо пропорциональной зависимостью между величинами, а две последние - с обратно пропорциональной.

В III классе рассматриваются преимущественно задачи с прямо пропорциональной зависимостью (I-IV виды), при этом рассматриваются задачи с такими группами величин: цена, количество, стоимость; масса одного предмета, число предметов, общая масса; ёмкость одного сосуда, число сосудов, общая ёмкость; выработка в единицу времени, время работы, общая выработка; расход материи на одну вещь, число вещей, общий расход материи. В IV классе рассматривается решение всех шести видов задач, вводятся новые группы величин: скорость, время, расстояние; длина прямоугольника, его ширина и площадь; урожай с единицы площади, площадь, весь урожай.

Таблица 1