Файл: Diskretnaya_matematika.doc

Следствие. Из теоремы 2 следует, что ес­ли в связном неориентированном мультиграфе имеются две вершины нечетной степени x_i и x_j, то сущест­вует эйлерова цепь, начинающаяся в х_i, и кончающаяся в x_j.

В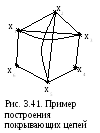качестве примера рассмот­рим граф на рис. 3.41. В нем х₁, х₂, х₃, х₅ – вершины нечет­­ной степени. Добавим два ребра: (х₂, х₅), (х₁ х₃) (штриховые линии). Получим эй­леров граф с эйлеровым циклом (x₁, x₂, х₃, х₄, х₅, х₂, x₅, х₆, х₁, х₃, х₁). Убрав (х₃, х₁), по­лу­чим эйле­рову цепь. Убрав (х₂, х₅), получим 2 по­крыва­ющих цепи: (x₁, х₂, х₃, х₄, х₅, х₂) и (х₅, х₆, х₁, х₃).

Рассмотрим теперь случай конечного ориентиро­ван­ного гра­фа. Чтобы в конечном ориентированном графе существовал эйлеров цикл(контур), необходимо и достаточно, чтобы полустепени исхо­да и захода вершин этого графа по входящим и исходящим дугам были равны:

m'(x_i) = m"(х_i),  x_i  X.

Доказательство то же, что и для неориентированного графа.

3.9.2. Гамильтоновы маршруты

Гамильтоновой цепью в неориентированном графе называет­ся цепь, проходящая через каждую его вершину один и только одинраз.

Гамильтоновым циклом в неориентированном графе назы­вается цикл, проходящий через каждую вершину один и только один раз за исключением начальной вершины, которая совпадает сконечной.

Гамильтоновым путем в ориентированном графе называетсяпуть S = (х₁, ..., х_n), проходящий через все вершины графа, притом только по одному разу.

Гамильтоновым контуром называется контур М=(х₀, х₁, ..., х_n,х₀) в ориентированном графе G(X), если он прохо­дит через все вер­шины графа по одному разу.

Существует следующая распространенная интерпре­тация зада­чи о гамильтоновых циклах. Обед накрыт на круглом столе. Среди гостей некоторые являются друзьями. При каких условиях можно рассадить всех так, чтобы по обе стороны от каждого из присутст­вующих сидели его друзья?

В применении графов к играм вершины соответствуют различ­ным позициям. Существование гамильтонова цикла равносильно существованию циклической после­довательности ходов, содержа­щей каждую позицию по одному разу. Примером является задача о шахматном коне: можно ли, начиная с произвольного поля на доске, ходить конем в такой последовательности, чтобы пройтикаждое из шестидесяти четырех полей и вернуться в исходное?

К гамильтоновым циклам относится также известная задача о бродячем торговце (задача о коммивояжере). Район, который дол­жен посетить коммивояжер, содержит определенное количество городов. Расстояния между ними известны, и нужно найти кратчай­шую дорогу, проходящую через все пункты и возвращающуюся в исходный. Эта задача имеет ряд приложений в экономике и иссле­довании операций.

Сформулирован целый ряд достаточных условий существова­ния гамильтоновых цепей, циклов, путей и контуров. Приведем не­которые из них без доказательства.

Теорема Кёнига. В полном конечном графе всегда существу­ет гамильтонов путь.

Если в графе G(X) с n вершинами для любой пары вершин x_i и x_j справедливо неравенство

m(х_i) + m(x_j)  n - 1,

где m(х_i), m(x_j) – степени вершин х_i и x_j, то граф G(X) имеет гамильтонову цепь.

Несмотря на сходство в определении эйлерова и гамильтонового циклов, соответствующие теории для этих понятий имеют мало общего. Критерий существования для эйлеровых циклов был уста­новлен просто, для гамильтоновых циклов никакого общего правиланеизвестно. Более того, иногда даже для конкретных графов бывает трудно решить, можно ли найти такой цикл. В принципе, поскольку речь идет о конечном числе вершин, задачу можно решить перебо­ром, однако эффективного алгоритма неизвестно.

3.10. Контрольные вопросы и упражнения

1. Покажите, что два графа на рис. 3.42 изоморфны.

Рис. 3.42. Граф к задаче 1

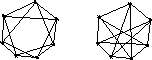
2. «Три дома и три колодца». Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?

3. Найдите число частичных графов конечного графа с m ребрами.

4. Каково число ребер в полном неориентированном графе с n вер­шинами?

5. Пусть U – множество положительных целых чисел, на котором задано отношение «а есть делитель b». Постройте граф этого от­ношения для множества целых чисел от 1 до 20.

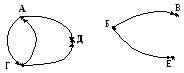
Рис.3.43. Граф к задаче 6

6. Задан граф отношения «быть сестрой» (рис. 3.43) на множестве студентов-родственников нашего фа-культета. Постройте по рис. 3.43 граф отношения «быть братом».

7. Постройте матрицы смежности и инциденций для правильных многогранников: тетраэдра, куба, октаэдра. Найдите для каждого из них число внутренней устойчивости, число внешней устойчи­вости, центр, периферийные вершины, радиус, диаметр.

8. Для графа, изображенного на рис. 3.44, найдите:

а) матрицу смежности (вершин);

б) матрицу инциденций;

в) наибольшее внутренне устойчивое множество;

г) наименьшее внешне устойчивое множество;

д) матрицу отклонений;

е) вектор отклоненностей;

ж) центр и радиус графа.

9. 

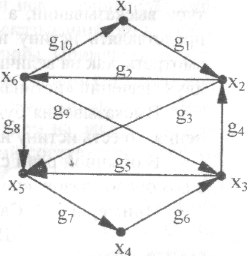
   Рис. 2.48 - К задаче 9

   

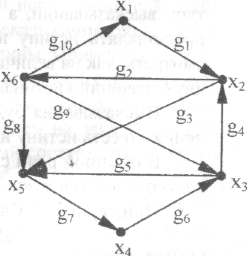
   Рис. 2.48 - К задаче 9

   

   

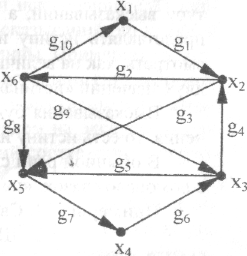
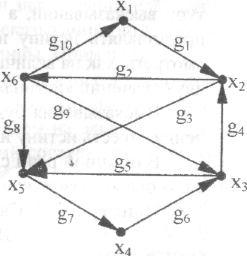
   Постройте графы, для которых радиус равен 2, 3, и такие графы, для которых диаметр равен 2, 3.

10. Определите, какие из графов трех правильных многогранников (тетраэдр, куб, откаэдр) имеют эйлеровы циклы. В тех случаях, когда эйлерова цикла нет, определите: сколько требуется цепей, чтобы покрыть все ребра графа.

11. Какие из из графов правильных многогранников имеют гамильтоновы цепи и циклы.

Список литературы

1. Адельсон-Вельский Г. М., Кузнецов О. П. Дискретная математика для инженера. – М. Энергоатомиздат, 1988.– 479 c.

2. Нефедов В. Н., Осипова В.А. Курс дискретной математики: Учебное пособие. – М.: Изд-во МАИ, 1992.– 262 с.

3. Ерусалимский Я. М. Дискретная математика: теория, задачи, приложения. – М: Вузовская книга, 2000.–280 с.

4. Новиков Ф. А. Дискретная математика для програм­мистов: Учебное пособие. – СПб: Питер, 2002. –304 с.

5. Хаггарти Р. Дискретная математика для программистов: Учебное пособие для вузов / Пер. с англ. – М.: Техносфера, 2003. – 320 с.

6. Корниенко А. В. Дискретная математика: Учебное пособие. – Томск: Изд-во ТПУ, 2000. – 104 с.

7. Сафьянова Е. Н. Дискретная математика. Часть 1: Учебное пособие. – Томск: Изд-во ТУСУР, 2000. – 106 с.

8. Смыслова З. А. Дискретная математика: Учебное пособие. – Томск: Изд-во ТУСУР, 2000. – 116 с.

108