ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.08.2024
Просмотров: 1731
Скачиваний: 0
СОДЕРЖАНИЕ
1.4. Декартово произведение множеств
1.5.1. Определение бинарного отношения
1.5.2. Способы задания бинарного отношения
1.5.3. Свойства бинарных отношений
1.5.4. Отношения эквивалентности
1.7. Контрольные вопросы и упражнения
2.1.1. Логические высказывания
2.1.2. Основные логические операции
2.2.1. Булевы функции и операции
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
2.3. Полные системы логических функций
Класс функций, сохраняющих ноль
Класс функций, сохраняющих единицу
Класс самодвойственных функций
2.4.3. Минимизация днф методом Квайна
2.6. Контрольные вопросы и упражнения
3.1.2. Ориентированные и неориентированные графы
3.1.4. Частичные графы и подграфы
3.1.6. Изоморфизм. Плоские графы
3.2. Отношения на множествах и графы
3.3. Матрицы смежности и инциденций графа
3.5.1. Степени неориентированных графов
3.5.2. Степени ориентированных графов
3.6.1. Характеристики расстояний в графах
3.6.2. Характеристические числа графов
3.7.2 . Базисные циклы и разрезающие множества
Свойства базисных циклов и разрежающих множеств
3.7.3. Цикломатическая матрица и матрица разрезов
Составление цикломатической матрицы
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
3.8.2. Алгоритм определения кратчайших путей
То есть, импликант Ul обращается в единицу на тех же наборах, что и дизъюнкция ядерных импликантов: не входит ни в одну из тупиковых ДНФ функции f(x1, ..., xn).
Возвращаясь к примеру 2, отметим, что:
Импликант х1х4удовлетворяет следствию из теоремы 8:
х1х4 х2х4 х1 х2 1
и поэтому не входит ни в одну тупиковую форму.
Импликант х2х3х4, для которого
х2х3х4х2х4х1х2≢1 не удовлетворяет следствию.
Импликантх1х3х4, для которого
х1х3х4х2х4 х1 х2 ≢1, не удовлетворяет следствию.
Импликантх1х2х3, для которого
х1х2 х3х2х4 х1 х2 ≢ 1, не удовлетворяет следствию.
Таким образом, последовательность действий при выполнении второго этапа состоит в следующем:
для каждого простого импликанта сокращённой ДНФ проверить, входит он в ядро или нет. Отметить неядерные импликанты;
проверить для отмеченных импликантов выполнение следствия из теоремы 8. Простые импликанты, для которых выполнено следствие, удалить из сокращённой ДНФ;
проверить возможность удаления оставшихся отмеченных конъюнкций. Из полученных тупиковых ДНФ выбрать минимальную ДНФ.
Рассмотрим эту последовательность действий на примере 2.
нашли ядро функции f(х1, х2, х3, х4), состоящее из простых импликантов х2х4 и х1 х2. Отметим курсивом в сокращённой ДНФ неядерные импликанты:
х2х4 х1х4 х1 х2 х2 х3 х4 х1 х3 х4 х1х2 х3;
среди помеченных импликантов нашли удовлетворяющий следствию из теоремы 8. Это импликант х1х4. Удалим его из сокращённой ДНФ:
х2х4 х1 х2 х2 х3 х4 х1 х3 х4 х1х2 х3;
для получения тупиковых ДНФ удаляем подмножества отмеченных импликантов. Можно удалить следующие подмножества:
{х2 х3 х4,х1 х3 х4,х1х2 х3}I, { х2 х3 х4,х1 х3 х4}II, { х2 х3 х4, х1х2 х3}III, {х1 х3 х4,х1х2 х3}IV, {x2 x3 x4 }V, {х1 х3 х4}VI, {х1х2 х3} VII.
При каждом удалении нужно проверять, представляет ли оставшаяся ДНФ функцию f(х1, х2, х3, х4).
Если удалить подмножество I, то получим ДНФ, не представляющую функциюf(х1, х2, х3, х4), так как на наборе {0,1,1,1} функция:
f (х1, х2, х3, х4) = 1, а х2х4 х1х2 = 0.
Если удалить подмножество II, то получим ДНФ, не представляющую функциюf(х1, х2, х3, х4), так как на наборе {0,1,1,1} функция
f(х1, х2, х3, х4) = 1, а х2х4 х1 х2 х1х2 х3 = 0.
Если удалить подмножество III, получим минимальную ДНФ функции f(x1, x2, х3, х4):
х2х4х1х2х1х3х4– минимальная ДНФ.
2.4.3. Минимизация днф методом Квайна
Существуют и другие методы, позволяющие независимо от исходной формы представления функции найти все ее тупиковые формы и выбрать из них минимальную. Одним из них является метод Квайна. В соответствии с этим методом отыскание минимальной ДНФ проводится в несколько этапов.
Первый этап. Функция, заданная в виде логической формулы произвольной формы, представляется в СДНФ. При этом:
последовательным применением эквивалентных преобразований логическая функция приводится к ДНФ, то есть к форме, не содержащей знаков отрицания над функциями, более сложными, чем один из аргументов;
каждый член ДНФ, представляющий собой конъюнкцию менее n членов (n – количество аргументов функции), развертывается в дизъюнкцию нескольких элементарных конъюнкций умножением на выражение вида (х1х1) • (х2х2)•…, тождественно равное единице;
приводятся, если возможно, подобные члены.
Второй этап. Отыскиваются все простые импликанты данной функции. Для этого выписываются все элементарные конъюнкции, входящие в СДНФ. Каждая из пар этих конъюнкций исследуется на возможность склеивания. Члены, участвовавшие хотя бы в одном склеивании, отмечаются, но не исключаются из дальнейших сравнений.
В результате выявляются группы конъюнкций, содержащие по (n- 1) члену. С этой группой конъюнкций проводится та же процедура, после которой получим группы конъюнкций, содержащие по (n- 2) членов и так далее, пока не останется ни одного члена, допускающего склеивания с каким либо другим членом.
Добавление к исходной ДНФ любого количества «склеенных» членов не изменяет вида функции. Последующее исключение всех членов, отмеченных в процессе склеивания, тоже не изменяет функцию, так как они поглощаются склеенными членами. Все неотмеченные в процессе преобразований члены представляют собой простые импликанты, а их дизъюнкция эквивалентна исходной функции.
Третий этап. Дизъюнкция всех простых импликантов может оказаться избыточной формой представления функции. Поэтому исследуется возможность удаления некоторых из них. Для этого составляется импликантная таблица, строки которой обозначаются выявленными на втором этапе простыми импликантами, а столбцы –элементарными конъюнкциями, входящими в СДНФ.
Любая клетка этой таблицы отмечается, если простой импликант, записанный в соответствующей строке, является составной частью элементарной конъюнкции, записанной в соответствующем столбце. Иначе говоря, данный простой импликант покрывает нашу функцию на наборе, соответствующем элементарной конъюнкции, записанной в столбце.
В каждом столбце при этом может оказаться несколько отмеченных клеток. Задача упрощения ДНФ сводится к вычеркиванию из таблицы максимального количества строк таким образом, чтобы заданная функция на всех наборах, обращающих ее в единицу, оказалась покрытой хотя бы одним простым импликантом.
Эту задачу можно выполнить в следующей последовательности:
выявляются столбцы, содержащие только одну помеченную клетку. Простые импликанты, соответствующие этим клеткам, записываются в окончательное выражение для ДНФ как обязательные члены. После этого в таблице вычеркиваются строки, соответствующие обязательным простым ипликантам и столбцы, содержащие отмеченные клетки в вычеркнутых строках. Вычеркивание столбцов возможно потому, что соответствующие им элементарные конъюнкции уже покрыты обязательными простыми импликантами, и поэтому их можно исключить из дальнейшего рассмотрения;
если после этого в таблице окажутся такие пары столбцов, что всем отмеченным клеткам второго столбца соответствуют в тех же строках отмеченные клетки первого столбца, а возможно, и некоторые другие отмеченные клетки, то первый столбец вычеркивается. Это возможно потому, что какую бы совокупность простых импликантов, покрывающую элементарную конъюнкцию, которая соответствует второму столбцу мы ни подобрали, этой совокупностью автоматически будет покрываться и конъюнкция, соответствующая первому столбцу;
строки, не содержащие после выполнения п.п. 1 и 2 ни одной отмеченной клетки, также вычеркиваются. Это возможно потому, что все конъюнкции, которые могут быть покрыты данным простым импликантом, уже покрыты другими простыми импликантами, которые должны войти в окончательное выражение для ДНФ;
в сокращенной таблице выявляется пара строк, содержащая хотя бы по одной отмеченной клетке в каждом столбце. Простые импликанты, соответствующие этим строкам, добавляются к ДНФ;
если оказывается несколько вариантов выполнения п. 4, то все они сравниваются, и выбирается простейший вариант.
Пример.Минимизировать функцию:
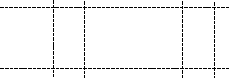
f(х1, х2, х3, х4) = х1 х2 х4 х2 х3 х4 х1х2 х3 х1х2х4.
В результате развертывания элементарных конъюнкций получим:
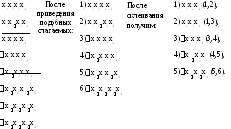
Таблица 2.7. Импликантная таблица
|
|
х1х2 х3 х4 |
х1х2х3 х4 |
х1 х2 х3 х4 |
х1х2 х3 х4 |
х1х2 х3х4 |
х1х2х3х4 |
|
|
Х |
Х |
|
|
|
|
|
х2 х3 х4 |
Х |
|
Х |
|
|
|
|
х1 х3 х4 |
|
|
Х |
Х |
|
|
|
х1х2 х3 |
|
|
|
Х |
Х |
|
|
х1х2х4 |
|
|
|
|
Х |
Х |
 х1
х2
х4
х1
х2
х4