ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.08.2024
Просмотров: 1742
Скачиваний: 0
СОДЕРЖАНИЕ
1.4. Декартово произведение множеств
1.5.1. Определение бинарного отношения
1.5.2. Способы задания бинарного отношения
1.5.3. Свойства бинарных отношений
1.5.4. Отношения эквивалентности
1.7. Контрольные вопросы и упражнения
2.1.1. Логические высказывания
2.1.2. Основные логические операции
2.2.1. Булевы функции и операции
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
2.3. Полные системы логических функций
Класс функций, сохраняющих ноль
Класс функций, сохраняющих единицу
Класс самодвойственных функций
2.4.3. Минимизация днф методом Квайна
2.6. Контрольные вопросы и упражнения
3.1.2. Ориентированные и неориентированные графы
3.1.4. Частичные графы и подграфы
3.1.6. Изоморфизм. Плоские графы
3.2. Отношения на множествах и графы
3.3. Матрицы смежности и инциденций графа
3.5.1. Степени неориентированных графов
3.5.2. Степени ориентированных графов
3.6.1. Характеристики расстояний в графах
3.6.2. Характеристические числа графов
3.7.2 . Базисные циклы и разрезающие множества
Свойства базисных циклов и разрежающих множеств
3.7.3. Цикломатическая матрица и матрица разрезов
Составление цикломатической матрицы
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
3.8.2. Алгоритм определения кратчайших путей
3.7.2 . Базисные циклы и разрезающие множества
Пусть T- остов графаG, аgi* – хорда кодереваT*. Так как Т – ацикличный граф, то граф Тgi* содержит точно один циклCi. ЦиклCiсостоит из хордыgi* и тех ветвей остова Т, которые образуют единственную простую цепь между концевыми вершинами хордыgi*. ЦиклCi, возникающий в графе Тgi*, называетсябазисным цикломотносительно хордыgi*остова Т. Множество всех таких циклов, число которых равно цикломатическому числуµ(G) графаG, называютбазисным множеством цикловграфаGотносительно остова Т.
Пусть G(X) – связный граф иX= {X1,X2} – некоторое разбиение множества его вершин:X=X1 X2 иX1X2 =. Множество ребер графаG, одна концевая вершина каждого из которых принадлежитX1, а другая –X2, называетсяразрежающим множествомилиразрезомграфа. Удаление разрежающего множества – разрез графа, разделяет граф на две компоненты и делает его несвязным.
Пусть T – остов связного графа G, а gj – ветвь этого остова. Удаление ветви из остова разбивает остов на 2 компоненты T1 и T2. Пусть X1 и X2 множества вершин, соответственно, компонент T1 и T2, а G1 и G2 – подграфы графа G, порожденные множествами вершин X1 и X2. Очевидно, что T1 – остов подграфа G1, а T2 – остов подграфа G2. Следовательно, подграфы G1 и G2 связны, а разрез, разделяющий X1 и X2, является разрежающим множеством графа G.
Разрежающее множество Sj, составленное из ребер, связывающих вершины компонент T1 и T2 остова называется базисным разрежающим множеством графа G. При этом, компоненты T1 и T2 остова образованы удалением ветви gj остова T.
Свойства базисных циклов и разрежающих множеств
1. Базисный цикл Ci относительно хорды gi* кодерева T* связного графа G включает точно те ветви остова T, которым соответствуют базисные разрежающие множества, включающие эту хорду.
2. Базисное разрежающее множество Sjотносительно ветвиgjостоваTсвязного графаGвключает точно те хорды кодереваT*, которым соответствуют базисные циклы, включающие эту ветвь.
3.7.3. Цикломатическая матрица и матрица разрезов
Рассмотренные ранее такие понятия как цикломатическое число и ранг, являются одними из важных числовых характеристик графов. Они определяют, соответственно, количество базисных циклов и базисных разрежающих множеств следующим образом:
1. Количество базисных циклов графа Gравно цикломатическому числу графа - числу ребер в кодереве.
2. Количество базисных разрежающих множеств равно величине ранга графа - числу ребер в остове.
Построим цикломатическую матрицу C= (cik) и матрицу разрезовS= (sjk) графа, элементы которых:
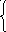
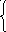 1,
еслиgk
Ci
; 1,
если gk
Sj
;
1,
еслиgk
Ci
; 1,
если gk
Sj
;
cik = sjk =
0, если gk Ci . 0, если gk Sj.
Каждая строка матриц CиSопределяет некоторый цикл и разрез графа. Количество строк этих матриц равно числу всех циклов и разрезов исходного графаGсоответственно. Эти строки матриц, а также соответствующие им циклы и разрезы, можно получить как суперпозицию базисных циклов и разрежающих множеств.
Суперпозиция осуществляется с помощью операции сложения по модулю 2 двоичной алгебры, обозначаемой символом . Вектор-строка сi= (ci1,ci2, …,cim), описывающая циклCiграфа, вычисляется как покомпонентная сумма по модулю 2 векторов, соответствующих базисным циклам. Аналогично, вектор-строкаsj= (sj1,sj2, …,sjm) описывает разрезSjграфа и вычисляется как сумма по модулю 2 векторов, соответствующих базисным разрезающим множествам.
Рассмотрим пример построения этих матриц для графа, приведенного на рис. 3.30. Сначала вычислим ранг и цикломатическое число этого. Ранг графа – число ребер в остове (рис. 3.31) – равен 4. Цикломатическое число графа – число ребер в кодереве (рис. 3.32) – равно 3. Следовательно, имеем 3 базисных цикла и 4 базисных разрезающих множества. Далее запишем эти базисные циклы и разрезающие множества.
Базисные циклы:
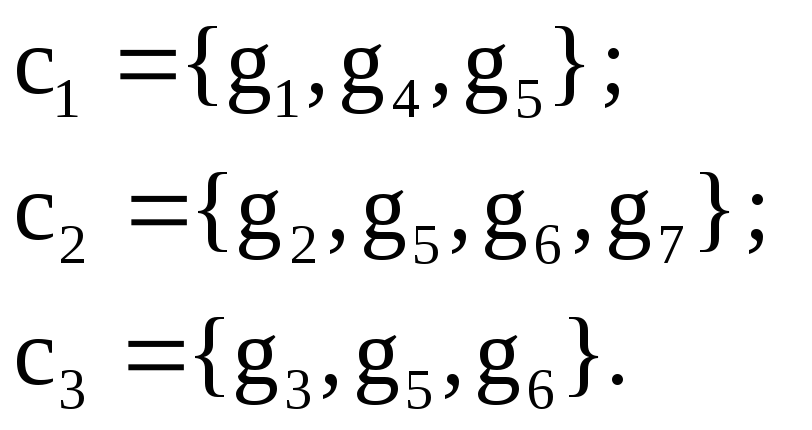
Базисные разрезающие множества:
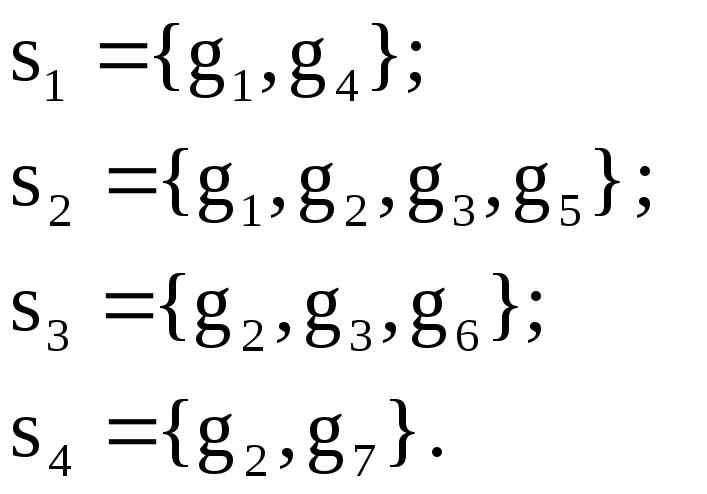
Составление цикломатической матрицы
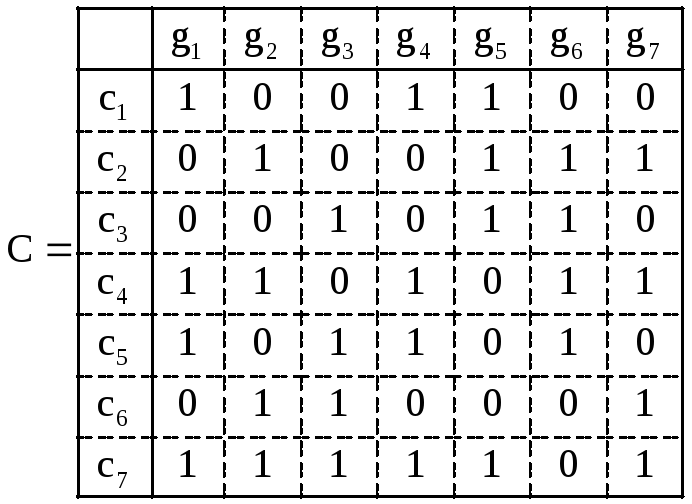
где
![]()
Составление матрицы разрезов
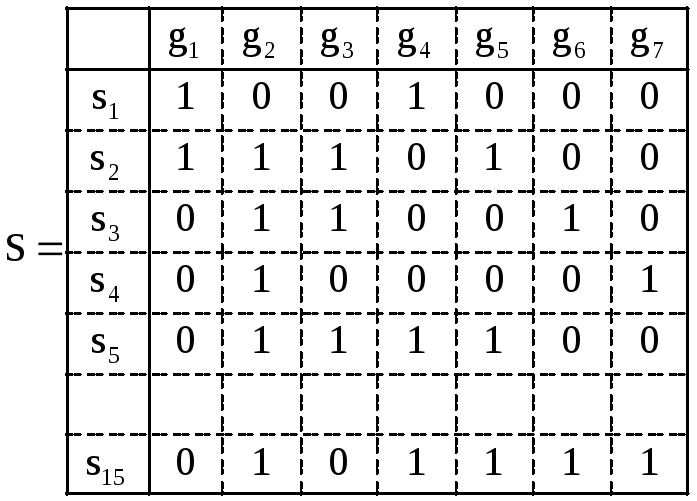
где
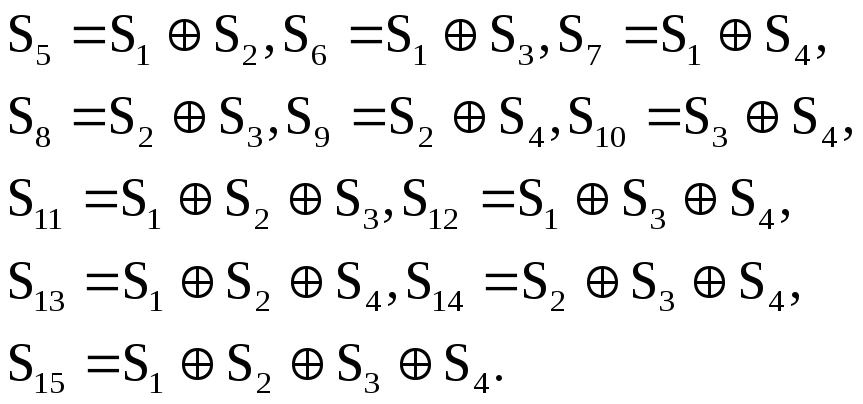
Замечание.Символ![]() обозначает операцию сложения по модулю
2. Результат этой операции равен 0, если
арифметическая сумма чисел есть четное
число, и равен 1–в противном случае.
обозначает операцию сложения по модулю
2. Результат этой операции равен 0, если
арифметическая сумма чисел есть четное
число, и равен 1–в противном случае.
Цикломатическая матрица Cи матрица разрезовSявляются ортогональными, что математически выражается матричным уравнением:CST=. ЗдесьST– транспонированная матрицаS, а– нулевая матрица.
Ортогональность матриц CиSобусловлена тем, что множество хорд, порождающих базисные циклы, и множество ветвей, порождающих базисные разрезающие множества, не пересекаются (рис. 3.30). Легко проверить ортогональность полученных матриц.
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
Решение целого ряда практических задач, описываемых в терминах графов, зависит от существования некоторой цепи, соединяющей данную вершину с какой-либо другой. Например, в качестве вершин графа можно рассматривать исходные позиции или состояния некоторой головоломки или игры, а ребра будут указывать возможные ходы из одной позиции в другую. Ребро будет неориентированным или ориентированным в зависимости от того, обратим переход или нет.
Граф G(X) с двумя отмеченными вершинамиxi,xjназывается (xi,xj) – плоским, если графG(X)=G(X)(xi,xj), полученный добавлением кG(X) ребра (xi,xj), является плоским.
Рассмотрим алгоритм определения пути, ведущего из вершины xiвxjплоского графа. Еслиxiне является вершиной никакого простого цикла, то при определении алгоритма пути изxiвxjв графеG(X) всегда выбирается самый левый или правый коридор (ребро) (рис. 3.33).
– путь при выборе
левого коридора;
путь при выборе
левого коридора;
– путь при выборе
правого коридора.
путь при выборе
правого коридора.
Аналогичный алгоритм определения пути в прадереве предполагает следующие действия. Из корня идти по какой-либо ветви насколько возможно далеко, затем возвратиться на какой-нибудь перекресток и отправиться по новому направлению (еще не пройденному) и т.д. Искомый путь из xiвxjбудет состоять из всех тех ребер, которые в процессе поиска были пройдены по одному разу.
При определении пути в произвольном графе, не являющемся прадеревом, приходим к предыдущему случаю следующим образом. Если, пройдя по некоторому ребру g, попадаем на уже пройденный ранее перекресток х, то реброg«отсекается» от одной из своих концевых точек. После отсечения ребра, пройденные хотя бы один раз, образуют прадерево.
 Рис.
3.33. Определение пути в графе
Рис.
3.33. Определение пути в графе
При определении пути в графе с помощью алгоритма Тарринеобходимо в данном алгоритме пользоваться правилом:
а) не проходить дважды по одному ребру в одном и том же направлении;
б) находясь в вершине х, не выбирать того ребра, которое привело в данную вершину в первый раз (если есть возможность другого выбора).
3.8.2. Алгоритм определения кратчайших путей
Эта задача имеет большое значение в практических применениях. К ней сводятся многие задачи выбора наиболее экономичного (с точки зрения расстояния или стоимости) маршрута на имеющейся карте дорог, наиболее экономичного способа перевода динамической системы из одного состояния в другое и т.д. Существует много математических способов решения, но часто методы, основанные на теории графов, наименее трудоемки.
Рассмотрим задачу о кратчайшем пути. Пусть дан графG(X), дугам которого приписаны веса (расстояния, стоимости и т.п.), задаваемые матрицей С = ||cij||.
Задача о кратчайшем пути состоит в нахождении кратчайшего пути от заданной начальной вершины sXдо заданной конечной вершиныt Xпри условии, что такой путь существует. В общем случае возможно Сij> 0, Сij < 0, Сij= 0. Единственное ограничение состоит в том, чтобы в графеG(X)не было цикловс отрицательным суммарным весом.
Приведем очень простой и эффективный алгоритм Дейкстрырешения этой задачи для случая Сij0i,j. Алгоритм основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины пути отsк этой вершине. Величины этих пометок постепенно уменьшаются с помощью некоторой итерационной процедуры, и на каждом шаге итерации точно одна из временных пометок становится постоянной. Это означает, что пометка уже не является верхней границей, а дает точную длину кратчайшего пути отsк рассматриваемой вершине. Пустьl(xi) – пометка вершиныxi. Опишем основные этапы алгоритма.