Файл: Diskretnaya_matematika.doc

Алгоритм Дейкстры

Шаг 1. Присвоение начальных значений. Для исход­ной вершиныsположимl(s) = 0 и эта пометка будет по­сто­янной. Для всех других вершин имеем: 1(х_i) =x_is. Эти пометки временные. Положимp=sи составим мно­жество образов этой вершины:G(p).

Шаг 2. Обновление пометок. Для всехx_iG(p), помет­ки которых являются времен­ными, изменить пометки в соответствии с выражением:

1(х_i) = min [1(х_i), 1(р) + c(p, x_i)] (8)

Шаг 3. Превращение пометок в постоянные. Среди всех вершин с временными пометками найти та­куюx_i^*, для которойl(x_i^*) =min[l(x_i)]. Считать пометку вершиныx_i^*постоянной и положить р =x_i^*.

Шаг 4. Переход к шагу 2, если р  t. Останов при р = t. В случае, если требуется найти лишь путь от s к одной вершине t, следует окончание счета. Длина этого крат­чайшего пути будет 1(р).

При необходимости нахождения путей от sко всем остальным вершинам графа переходим к шагу 2. Продолжаем вычисления, пока все вершины не получат по­стоянные пометки. Эти отметки и дают длины кратчайших путей отsк этим вершинам.

Проиллюстрируем работу алгоритма на примере графа, изо­браженного на рис. 3.34. Матрица весов – в табл. 3.4. Граф является смешанным, т. е. ребра у него ориентирова-нные и неори­ентированные. Требуется найти все кратчайшие пути от x₁ко всем остальным вершинам. Постоянные пометки будем обозначать знаком⁺.

Шаг 1.l(x₁) = 0⁺, 1(x_i) =x_ix₁, р =x₁.

Первая итерация

Шаг 2.G(p) =G(x₁) = {х₂, х₇, х₈, х₉}. Все эти вершины имеют временные пометки.

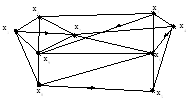
Рис.3.34. Пример графа к алгоритму Дейкстры

В соответствии с формулой (8) уточняем пометки:

l(х₂) = min(, 0⁺ + 10) = 10; l(х₇) = 3; l(х₈) = 6; l(x₉) = 12.

Шаг 3.min(10, 3, 6, 12,) = 3

х₂ х₇ х₈ х₉ х₃, х₄, х₅, х₆

Вершина х₇ получает постоянную пометку: 1(х₇) = З⁺ .

Далее р = x₇.

Шаг 4. Так как не все вершины имеют постоянные пометки, то переходим к шагу 2. На рис. 3.35 приведены значения пометок вершин графа. Здесь выделены вершины с постоянными пометками.

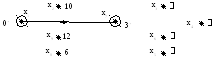
Рис. 3.35. Пометки в начале второй итерации

Вторая итерация

Шаг 2.G(p) =G(x₇) = {х₂, х₄, х_б, х₉}.Пометки всех этих вершин временные. Из (8) получим:l(х₂) = 5,l(х₄) = 7,l(х₆)=17,l(х₉) = 12.

Шаг 3.min(5, 7, 17, 6, 12,) = 5.

х₂ х₄ х₆ х₈ х₉ х₃, х₅

Вершина х₂ получает постоянную пометку 1(х₂) = 5⁺.

Далее р = x₂.

Шаг 4. Значения пометок приведены на рис. 3.36. Переходим к шагу 2.

Рис. 3.36. Пометки в начале третьей итерации

Третья итерация

Шаг 2.G(p) =G(x₂) = {х₁, х₃, х₇, х₉}. Только вершины х₃и х₉ имеют временные пометки. Из (8) получим:l(х₃) =min(,5⁺+18) = 23, аналогично 1(х₉) =12.

Шаг 3.min(23, 7, 17, 6, 12,) = 6,

х₃ х₄ х₆ х₈ х₉ х₅

Вершина х₈ получает постоянную пометку 1(х₈) = 6⁺, р=x₈.

Шаг 4. Перейти к шагу 2 (рис. 3.37).

Рис. 3.37. Пометки в начале четвертой итерации

Продолжая итерационный процесс, получим в итоге постоян­ные пометки для всех вершин графа (рис.3.38) и кратчайшие пути от вершины х₁ко всем остальным вершинам. Эти пути выделены жирными линиями.

Для нахождения кратчайшего пути между вершиной х₂и на­чальной вершинойх₁последовательно используем соотношениеl(х_i) + С(х_i, х_i) =l(х_i). Полагаяi= 2 находим вершину х₂', непосред­ственно предшествующей х₂в кратчайшем пути от х₁к х₂:

1(х₂') + С(х₂', х₂) =l(х₂) = 5. Этому соотношению удов­ле­­творяет вершина х₇. Следовательно, х₂' = х₇. Полагаяi= 7 и применяя соот­ношение еще раз, получим х₇' = х₁Поэтому кратчайший путь со­стоит из вершин х₁, х₇, х₂. Аналогичным образом находим все крат­чайшие пути от х₁к остальным вершинам.

Рис. 3.38. Пометки и кратчайшие пути в графе

3.9. Обход графа

В теории графов есть понятие обход графа. Это маршрут, содержащий все ребра или вершины графа и обладающий определенными свойствами. Наиболее известными обходами графа являются эйлеровы и гамильтоновы цепи и циклы.

3.9.1. Эйлеровы маршруты

Эти понятия возникли в статье Эйлера в 1735 г., в которой он решал задачу о Кенигсбергских мостах и впервые ввел понятие графа. На рис. 3.39, а приведен план расположения семи мостов в Кенигсберге (ныне Калининграде). Задачасостоит в том, чтобы пройти каждый мост по одному разу и вер­нуться в исходную точку С. Поскольку в конце обхода нужно вернуться в исходную часть города, и на каждом мосту нужно побывать по одному разу, этот маршрут является простым циклом, содержащим все ребра графа. В дальнейшем такие циклы стали называть эйлеровыми, а графы, имеющие эйлеров цикл – эйлеровыми графами.

а) б)

Рис. 3.39. Схема Кенигсбергских мостов и соответствующий граф

Эйлеров цикл можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги. Таким образом, эйлеровы графы – это графы, которые можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной и той же точке.

Обнаружив, что в данном графе не существует циклических обходов, проходящих по всем ребрам по одному разу, Эйлер обра­тился к общей задаче: при каких условиях в графе можно найти та­кой цикл? Ответ на этот вопрос дает следующая теорема.

Теорема 1 (Эйлера). Конечный связный неориен­тиро­ванный мультиграф является эйлеровым графом тогда и только тогда, когдав нем отсутствуют вершины нечетной степени.

Доказательство. Каждый раз, когда эйлеров цикл проходит через какую-либо вершину, он должен войти в нее по одному ребру, а выйти по другому. Поэтому условие отсутствия вершин нечетнойстепени в эйлеровом графе является необходимым.

Для доказательства достаточности предположим, что всевершины графа имеют четные степени. Начнем цепь Р в произволь­ной вершине х_iграфаG(рис. 3.40, а), и будем продолжать ее, на­сколько возможно, все время через новые ребра. Так как в каждой вершине число ребер четно, этот процесс может закончиться тольков x_i. Если цикл Р содержит не все ребра графа G, то удалим из G часть, соответствующую циклу Р. Графы Р и G имеют четные степени всех вершин. То же долж­но быть справедливо и для оставшегося графа Р.

а) б)

Рис. 3.40. Иллюстрация доказательства теоремы Эйлера (а) и пример построения эйлерова цикла (б)

Так как граф Gсвязен, в циклеPдолжна найтись вершинаx_j,инцидентная также ребрам Р. Из х_j можно построить новую цепь Р', содержащую только ребра изР. И снова такая цепь может за­кончиться только при возвращении в х_j .

Процесс построения эйлерова цикла иллюстрирует рис. 3.40, б. Объединяя, например, циклы (x₁, х₂, х₃, х₄, х₅, х₆,x₁) и (х₃, х₇, х₈,x₃,x₅, x₁ x₃), получим эйлеров цикл (x₁, x₂, x₃, x₇, x₈, х₃, х₅, х₁, х₃, х₄, х₅, х₆, x₁).

Как граф с эйлеровым циклом можно рассмотреть схему обхо­да выставки по различным коридорам, которую посетители должныпройти согласно указателям так, чтобы увидеть каждый экспонат по одному разу.

Эйлеровой цепью называется цепь, включающая все ребра данного конечного неориентированного графаG(X), но имеющаяразличные начало x_i и конец x_j. Чтобы в графе существовала эйлеро­ва цепь, он должен быть связным и все вершины в нем, кроме х_i и x_j, долж­ны иметь четные степени. Степени вершин х_i и x_j должны быть не­четными, что естественно, так как из x_i мы лишний раз выходим, а в x_j мы лишний раз входим. Эти условия являются достаточными для существования эйлеровой цепи.

Важен также следующий вопрос: каково наименьшее количе­ство не пересекающихся по ребрам цепей, покрывающих конеч­ный связный граф G(X) (покрыть – значит включить все ребра графа в цепь)? На этот вопрос отвечает теорема 2.

Теорема 2.В конечном связном неориентированном графеG(X) сkвершинами нечетной степени минимальное число непере­секающихся по ребрам цепей, покрывающих G(X) равно k/2.

Доказательство. Пусть G(X) не является эйлеро­вым графом и k– число его вершин нечетной степени. Ранее было доказано, чтоkчетно. Каждая вершина нечетной степени должна быть концом хотя бы одной из покрывающих граф цепей. Следовательно, число такихцепей не меньше, чем k/2. Но можно показать, что и не больше. Со­единим попарно вершины нечетной степени k/2 ребрами. Тогда сте­пень каждой вершины увеличится на единицу и станет четной. По­лучится эйлеров граф, в котором существует эйлеров цикл. Теперь будем постепенно выбрасывать присоединенные ребра. При выбра­сывании первого ребра эйлеров цикл превратится в эйлерову цепь, апри выбрасывании каждого последующего ребра одна из возникших к этому моменту цепей разобьется на две части. Таким образом, об­щее число этих цепей равно k/2.