Файл: Diskretnaya_matematika.doc

X X = X,

X X = X;

б) коммутативность

X Y = YX,

X Y = YX;

в) ассоциативность

(X  Y)  Z = X  (Y  Z),

(X  Y)  Z = X  (Y  Z);

г) дистрибутивность

X  (Y  Z) = (X  Y)  (X  Z),

X  (Y  Z) = (X  Y)  (X  Z);

д) принцип двойственности (закон де Моргана)

X Y =XY,

XY =XY.

1.3. Системы множеств

Элементы множества сами могут быть множествами.

Пример 1.МножествоX= {1},{2,3},{1,2} состоит из

множеств:

Х₁ = {1}; Х₂ = {2,3}; Х₃ = {1,2}.

В этом случае будем говорить о системе множеств. Рассмотрим такие системы:булеаниразбиениемножеств.

Булеаном В(Х) множества X называется множество всех его подмножеств. В булеан В(Х) обязательно включается само множество X и пустое множество .

Пример 2. Для множества X = {0,1} булеаном является множе­ство:

В(Х) =, {0},{1},{0,1} .

Разбиением P(X) множества Х называется система его непустых непере­секающихся подмножеств, в объединении дающая множествоX(рис. 1.6).

Рис. 1.6. Разбиение множества P(X) = {Х₁, Х₂, Х₃, Х₄}

Разбиение P(X) = {Х₁, Х₂, ..., Х_n} множества X удовлетворяет следующим условиям:

1. X_i  X, i = l, ... , n;

2. X_i  , i = l, ... , n;

3. X_i  X_j = , при i  j;

4. 

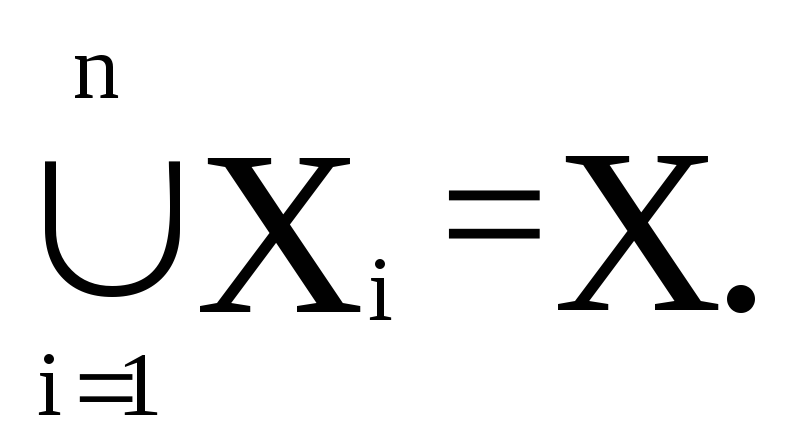
Множества Х₁, Х₂, ..., Х_nназываютсяблокамиразбиенияP(X). Для исходного множества Х можно получить несколько различных разбиений.

Пример 3. Для множества X = {1,2,3,4,5} можно построить следующие разбиения:

P₁(X) = {{1,2}, {3,4,5}} – из двух блоков;

P₂(Х) = {{1},{2,5},{3},{4}} – из четырех блоков.

Примерами разбиений также являются разбиения множества студентов университета по факультетам, по курсам и по группам.

1.4. Декартово произведение множеств

Декартовым произведениемXY двух множеств X и Y называется множество всех упорядоченных пар (x, у) таких, чтоxX, а уY .

Пример 1. Пусть: X = {1,2}, Y = {-1,0,1} .

X Y = (1,-1), (1,0), (1,1), (2,-1), (2,0), (2,1) ,

Y  X = (-1,1), (-1,2), (0,1), (0,2), (1,1), (1,2) .

Очевидно, что для операции декартова произведе­ния множеств закон коммутативности не выполняется:

X  Y  Y  X

Декартовым произведением множеств X₁, X₂, …, X_nбудем называть множество X₁X₂…X_n всех упорядоченных наборов (х₁, х₂ , …, х_n) таких, что:

x_iХ_i ; i = 1, 2 ,…,n.

Пример 2. X = {x₁, x₂, x₃, x₄} и Y = {у₁, у₂, у₃}. Декартово произведение X  Y представлено таблицей 1.1.

Таблица 1.1. Пример декартова произведения

Наглядно декартово произведение множеств можно представить в виде графика (рис. 1.7). Здесь кружочками отмечены элементы множества X Y = {1,2,3}{2,4}.

Рис. 1.7. График декартова произведения Х  Y

1.5. Бинарные отношения

1.5.1. Определение бинарного отношения

Пусть среди трех людей: Андрей (А), Василий (В) и Сергей (С) двое знакомы друг с другом (Андрей и Василий) и знают третьего – Сергея, но Сергей их не знает. Как описать отношения между этими людьми?

Имеем исходное множество Х = {А, В, С}. Далее из элементов множества Х составим упорядоченные пары: (А, В), (В, А), (А, С), (В, С). Это множество пар и описывает связи между элементами множества X. Кроме того, множество этих пар есть подмножество декартова произведенияXX.

Определение. На множестве X задано бинарное отношение R, если задано подмножество декартова произведения X  X (т. е. R  X  X).

Пример 1. Пусть X = {1, 2, 3, 4}. Зададим на X следующие отношения:

Т = {(х, у) | х, у Х; х = у} – отношение равенства;

Р = {(х, у) | х, у Х; х = у - 1} – отношение

предшествования;

Q= {(х, у) | х, уХ; х делится на у} – отношение

делимости.

Все эти отношения заданы с помощью характеристического свойства. Перечислим элементы этих отношений для заданного множества X = {1,2,3,4}:

Т = {(1,1), (2,2), (3,3), (4,4)};

P= {(1,2), (2,3), (3,4) };

Q= {(4,4), (4,2), (4,1), (3,3), (3,1), (2,2), (2,1), (1,1)}.

Тот факт, что пара (х, у) принадлежит данному отношению R, будем за­писывать: (х, у)RилиxRy. Например, для отношенияQзапись 4Q2 озна­чает, что 4 делится на 2 нацело, т. е. (4,2)Q.

Областью определенияD_r бинарного отношенияRназывается мно­жествоD_R= {x| (х, у)R}.

Областью значенийЕ_Rбинарного отношенияRназывается множество Е_R= {у| (х, у)R}.

В примере для отношения Р областью определения является мно­жество D_R= {1,2,3}, а областью значений является мно­жество Е_R= {2,3,4}.

1.5.2. Способы задания бинарного отношения

Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Существуют и более наглядные способы задания бинарного отношения: график отношения, схема отношения, граф отношения, матрица отношения.

График отношения изображается в декартовой системе координат: на горизонтальной оси отмечается область определения, на вертикальной - об­ласть значений отношения. Элементу отношения (х, у) соответствует точка плоскости с этими координатами.

a б

Рис. 1.8. График отношения Q (а) и схема отношения Q (б)

Схемаотношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент (х, у) принадлежит отношениюR, то соответствующие точки изD_Rи Е_Rсоединяются прямой.

ГрафотношенияR  X  Xстроится следующим образом. На плоско­сти в произвольном порядке изображаются точки - элементы множестваX. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара (х, у) принадлежит отношениюR.

МатрицаотношенияR  X  X– это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множестваX. На пересечении строки х и столбца у ставится 1, если пара (х, у)R; все остальные элементы матрицы заполняются нулями. Элементы матрицы нуме­руются двумя индексами, первый равен номеру строки, второй – номеру столбца.

Пусть X= {х₁, х₂, …, х_n} . Тогда матрица отношенияR  X  Xимеетnстрок иnстолбцов, а ее элементr_ijопределяется по правилу:

1

r_ij =

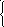
0, если (x_i, y_j)  R.

Рис. 1.9. Граф отношения Q (а) и матрица отношения Q (б)

1.5.3. Свойства бинарных отношений

1. Отношение Rна множествеXназываетсярефлексивным, если для всех хXвыполняется условие (х, х)R. ОтношениеRна множестве Х называетсянерефлексивным, если ус­ловие (х, х)Rне выполняется хотя бы при одном хX.