ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.08.2024
Просмотров: 1752
Скачиваний: 0
СОДЕРЖАНИЕ
1.4. Декартово произведение множеств
1.5.1. Определение бинарного отношения
1.5.2. Способы задания бинарного отношения
1.5.3. Свойства бинарных отношений
1.5.4. Отношения эквивалентности
1.7. Контрольные вопросы и упражнения
2.1.1. Логические высказывания
2.1.2. Основные логические операции
2.2.1. Булевы функции и операции
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
2.3. Полные системы логических функций
Класс функций, сохраняющих ноль
Класс функций, сохраняющих единицу
Класс самодвойственных функций
2.4.3. Минимизация днф методом Квайна
2.6. Контрольные вопросы и упражнения
3.1.2. Ориентированные и неориентированные графы
3.1.4. Частичные графы и подграфы
3.1.6. Изоморфизм. Плоские графы
3.2. Отношения на множествах и графы
3.3. Матрицы смежности и инциденций графа
3.5.1. Степени неориентированных графов
3.5.2. Степени ориентированных графов
3.6.1. Характеристики расстояний в графах
3.6.2. Характеристические числа графов
3.7.2 . Базисные циклы и разрезающие множества
Свойства базисных циклов и разрежающих множеств
3.7.3. Цикломатическая матрица и матрица разрезов
Составление цикломатической матрицы
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
3.8.2. Алгоритм определения кратчайших путей
Содержание
ВВЕДЕНИЕ 5
1. ТЕОРИЯ МНОЖЕСТВ 6
1.1. Основные определения 6
1.2. Операции над множествами 8
1.3. Системы множеств 12
1.4. Декартово произведение множеств 13
1.5. Бинарные отношения 15
1.5.1. Определение бинарного отношения 15
1.5.2. Способы задания бинарного отношения 16
1.5.3. Свойства бинарных отношений 18
1.5.4. Отношения эквивалентности 19
1.6. Отображения множеств 20
1.7. Контрольные вопросы и упражнения 22
2. МАТЕМАТИЧЕСКАЯ ЛОГИКА 24
2.1. Алгебра логики 24
2.1.1. Логические высказывания 24
2.1.2. Основные логические операции 25
2.1.3. Формулы алгебры логики 27
2.1.4. Логические функции 30
2.2. Булева алгебра 33
2.2.1. Булевы функции и операции 33
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы 34
2.3. Полные системы логических функций 38
2.4. Задача минимизация ДНФ 43
2.4.1. Основные определения 43
2.4.2. Этапы минимизации 44
2.4.3. Минимизация ДНФ методом Квайна 49
2.5. Синтез логических схем 53
2.6. Контрольные вопросы и упражнения 57
3. ТЕОРИЯ ГРАФОВ 59
3.1. Основные определения 60
3.1.1. Общие понятия 60
3.1.2. Ориентированные и неориентированные графы 61
3.1.3. Маршруты в графах 63
3.1.4. Частичные графы и подграфы 65
3.1.5. Связность в графах 67
3.1.6. Изоморфизм. Плоские графы 69
3.2. Отношения на множествах и графы 70
3.3. Матрицы смежности и инциденций графа 72
3.4. Операции над графами 74
3.4.1. Сумма графов 74
3.4.2. Пересечение графов 76
3.5. Степени графов 77
3.5.1. Степени неориентированных графов 77
3.5.2. Степени ориентированных графов 79
3.6. Характеристики графов 80
3.6.1. Характеристики расстояний в графах 80
3.6.2. Характеристические числа графов 82
3.7. Циклы и разрезы графа 84
3.7.1. Остов и кодерево 84
3.7.2. Базисные циклы и разрезающие множества 85
3.7.3. Цикломатическая матрица и матрица разрезов 87
3.8. Задача определения путей в графах 90
3.8.1. Определение путей в графе 90
3.8.2. Алгоритм определения кратчайших путей 91
3.9. Обход графа 96
3.9.1. Эйлеровы маршруты 97
3.9.2. Гамильтоновы маршруты 101
3.10. Контрольные вопросы и упражнения 103
СПИСОК ЛИТЕРАТУРЫ 105
ВВЕДЕНИЕ
Для создания и эксплуатации сложных автоматизированных систем обработки информации и их компонент в области экономики, математического и программного обеспечения вычислительной техники, сетей передачи данных и многих других сферах деятельности человека необходимо знание дискретной математики.
Дискретная математика – часть математики, которая зародилась в глубокой древности. Как говорит само название, главной ее особенностью является дискретность, т. е. антипод непрерывности. В ней отсутствует понятие предельного перехода, присущее классической, «непрерывной» математике. Дискретная математика занимается изучением дискретных структур, которые возникают как внутри математики, так и в ее приложениях.
Цель дисциплины «Дискретная математика» – знакомство с основными разделами этой науки: теорией множеств, математической логикой и теорией графов.
Дискретная математика является обязательной дисциплиной цикла «Математические и общие естественнонаучные дисциплины». Знания и навыки, полученные при ее изучении, используются в дисциплинах: «Информатика», «Теория алгоритмов» и т.д.
Данное пособие предназначено для иностранных студентов, обучающихся в Томском политехническом университете по специальностям: 351400 – прикладная информатика (в экономике); 220400 – программное обеспечение вычислительной техники и автоматизированных систем.
1. Теория множеств
1.1. Основные определения
Понятие множества являетсяфундаментальным понятием в математике. Под множеством понимают совокупность вполне определенных объектов, рассматриваемых как единое целое. Отдельные объекты, из которых состоит множество, называют егоэлементами. Природа объектов может быть самой различной. Например, можно говорить о множестве натуральных чисел, букв в алфавите, множестве стульев в комнате, студентов в группе, людей, живущих в Томске и т. п.
Для обозначения конкретных множеств принято использовать прописные буквы A,S,X, ... Для обозначения элементов множества используют строчные буквыa,s, х,…
Множество X, элементами которого являются х1, х2, х3, обозначают:X= {x1,x2, х3}. Это первый способ задания множества– перечисление всех его элементов. Он удобен при рассмотрении конечных множеств, содержащих небольшое число элементов.
Второй способ задания множества – описательный. Он состоит в том, что указывается характерное свойство, которым обладают все элементы множества.
Для указания того, что элемент х принадлежит множеству X, используется запись хX. Запись хXозначает, что элемент х не принадлежит множествуX.
Так, если М – множество студентов группы, то множество Xотличников этой группы записывается в виде
X = {х М | х – отличник группы}.
Это читается следующим образом: множество Xсостоит из элементов х множества М таких, что х является отличником группы.
Известные числовые множества обозначим следующим образом:
N= {1, 2, 3, …} – множество натуральных чисел;
Z= {…, -2, -1, 0, 1, 2, …} – множество целых чисел;
Q– множество рациональных чисел;
R– множество действительных чисел.
Множество, не содержащее ни одного элемента, называется пустым. Пустое множество обозначается.
Пример.X= {хZ| х2 - х + 1 = 0} =.
Множество Xявляетсяподмножеством множестваY, если любой элемент множестваXпринадлежит множествуY. Этот факт записывается какXY.
Два множества XиYравны в том случае, когда они состоят из одних и тех же элементов. РавенствоX=Yозначает: если хX, то хYи если уY, то уX.
Для сокращения записи в теории множеств используются некоторые логические символы. Это символы общности и существования, а также символы следствияи эквивалентности.
Смысл этих обозначений следующий:
– «любой», «каждый», «для всех»;
– «существует», «найдется», «хотя бы один»;
– «следует», «влечет»;
– «эквивалентно», «необходимо и достаточно».
Рассмотрим примеры использования этих символов.
1. Определение подмножества X Y приводит к записи:
х [х X х Y].
2. Определение равных множеств X=Y приводит к записи: X = Y X Y и Y X.
Множество называется конечным, если оно содержит конечное число элементов, ибесконечным, если число его элементов бесконечно.
1.2. Операции над множествами
Над множествами можно производить действия, которые во многом напоминают действия сложения и умножения в элементарной алгебре. Для графической иллюстрации операций над множествами будем использовать так называемые диаграммы Эйлера, в которых произвольному множеству X ставится в соответствие множество точек на плоскости внутри некоторой замкнутой кривой.
Объединением(суммой) множествXиYназывают множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множествX,Y(рис. 1.1).
Р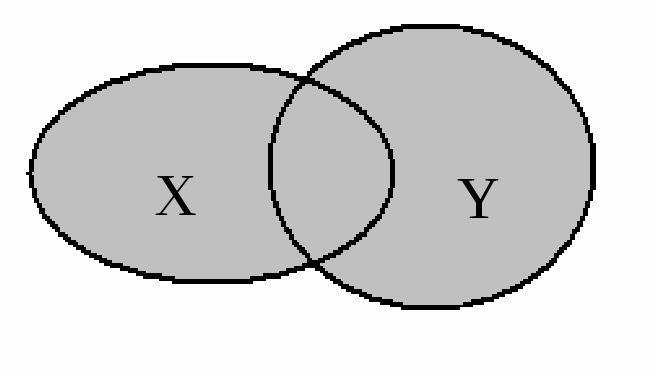 ис.
1.1. Объединение множеств
ис.
1.1. Объединение множеств
Объединение двух множеств символически записывают как X Y. Объединение множеств Xi (i = 1, 2, ..., n) есть множество элементов, каждый из которых принадлежит хотя бы одному из множеств Xi. Соответствующее обозначение:
![]()
Пересечением множествXиYназывают множество, состоящее из всех тех элементов, которые принадлежат какмножеству X, так и множеству Y (рис. 1.2).
Р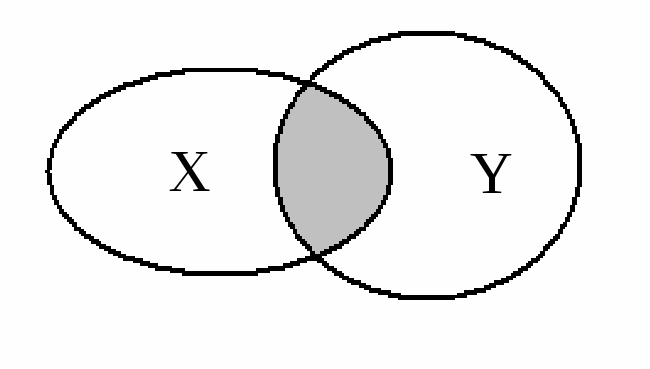 ис.
1.2. Пересечение
множеств
ис.
1.2. Пересечение
множеств
Пересечение множеств обозначается через X Y. Множества X и Y называют непересекающимися, если они не имеют общих элементов, т.е. если X Y = .
Пересечением множеств Хi (i = 1, 2, ..., n) называется множество элементов, принадлежащих каждому Xi. Оно обозначается как
![]()
Разностью множеств X и Y называют множество, состоящееиз всех тех элементов, которые принадлежат X и не принадлежат Y (рис. 1.3). Разность множеств обозначается через X \ Y. Очевидно, что X \ Y Y \ X.
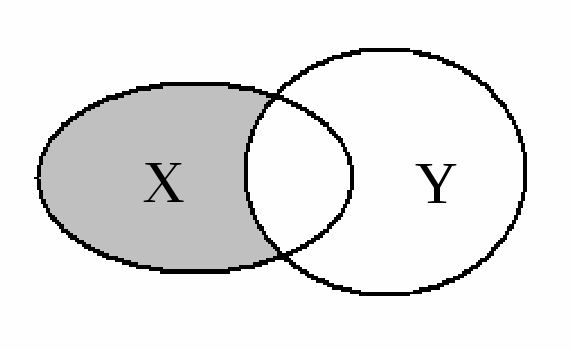
Рис. 1.3. Разность множеств
Симметрической разностью X⊕Y множеств X и Y называется объединение разностей X\Y иY\X. Эта разность множеств является составной операцией:
X ⊕ Y = (X \ Y) (Y \ X).
Пример 1. Пусть: X – множество отличников в группе, Y – множество студентов, живущих в общежитии. Тогда: X Y – множество студентов, которые или учатся на «отлично», или проживают в общежитии; X Y – множество отличников, живущих в общежитии; X \ Y – множество отличников, живущих вне общежития.
Дополнительным кмножеству X по отношению к множествуW, еслиX W, называется множество, состоящее из элементов W, не принадлежащих множествуX. Дополнительное множество обозначается:Zw(X) (рис. 1.4).
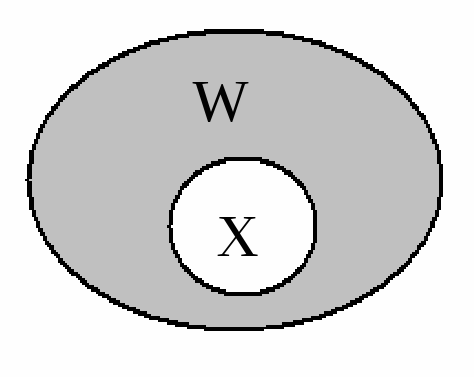
Рис. 1.4. Дополнительное множество
Универсальным множеством называется множество I, для которого справедливо соотношение:XI=X. Оно означает, что множество I содержит все элементы множества X. Следовательно, любое множество X полностью содержится во множестве I, т.е. является его подмножеством: Х I. Так, для примера 1 универсальным множеством можно считать множество студентов в группе.
Универсальное множество удобно изображать графически в виде множества точек прямоугольника. Отдельные области внутри этого прямоугольника будут представлять подмножества универсального множества.
Дополнением множества X (до универсального множества I) называют множество Х, определяемое из соотношения: Х = I \ X.
На рис 1.5 множествоХ представляет собой не заштрихованную область.
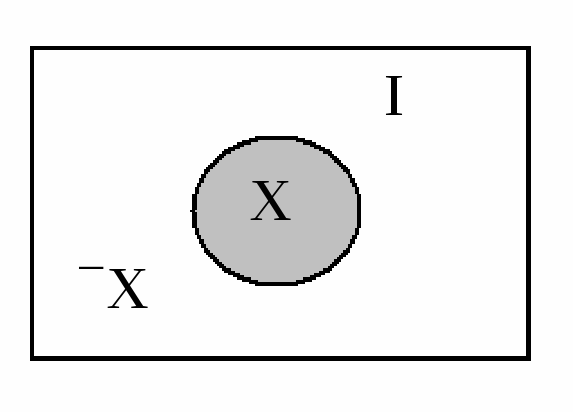
Рис. 1.5. Множество Х и его дополнениеХ
Очевидно выполнение соотношений:
X Х = , X Х = I.
Из этого следует,
что само множество X, в свою очередь,
является дополнением множества Х
(до I).
Следовательно:
![]()
С помощью операции дополнения можно представить разность множеств в виде составной операции:
X \ Y = X Y.
Свойства операций над множествами
а) идемпотентность