Файл: деп_тукс_10_11.doc

Настоящая квантовая теория начинается там, где появляются несепарабельные состояния. Причем речь идет не о каких-то «интерпретациях», в которых эта несепарабельность (квантовая запутанность) вводится с некой «хитрой» целью, а о стандартной квантовой теории, и наличие несепарабельных состояний — это естественное следствие основного принципа квантовой механики — принципа суперпозиции состояний.

Т.о., несепарабельные состояния отдельной системы никакими ухищрениями типа статистической (ансамблевой) интерпретации невозможно свести к привычным классическим представлениям и сепарабельным состояниям.

В квантовой теории известен принцип несепарабельности: если две системы взаимодействовали в прошлом, то в общем случае невозможно приписать один вектор состояния любой из двух подсистем.

Этот принцип является прямым следствием общих правил квантовой механики. Принцип является всеобщим, и взаимодействия могут быть любого рода, между любыми системами.

Принцип несепарабельности — самый общий, и обычно мы имеем дело с целым набором самых различных взаимодействий с окружением, при этом отдельным взаимодействиям соответствует своя степень квантовой запутанности (несепарабельности). Вот почему в «игру» вступают относительные величины квантовой запутанности. Для сильных классических взаимодействий сепарабельность выше, поэтому хорошо работает приближение, не принимающее во внимание квантовую запутанность в классической физике. Однако подсистемы могут находиться в практически сепарабельном состоянии по одним степеням свободы, но несепарабельны по другим. Например, мы сепарабельны (разделены) в своих физических телах, но в какой-то мере несепарабельны по чувствам и еще более — по мыслям.

В настоящее время под «квантовой системой» в общем случае понимается любая система, описываемая в терминах состояний, то есть посредством «вектора состояния», «матрицы плотности» и т. д. Это наиболее полное описание. А классическая физика для макросистем — лишь частный случай квантового описания, предельный случай, когда мы пренебрегаем несепарабельностью. Вся классическая физика — это сепарабельное описание.

Макросистемы отличаются от микрочастиц только в одном плане — на микроуровне эффекты несепарабельности выражены наиболее явно, для микрочастиц квантовые корреляции сравнимы с классическими взаимодействиями, поэтому без запутанности тут уже не обойтись.

«Вычеркнуть» запутанность очень просто — достаточно ею пренебречь и не принимать во внимание.

Несепарабельные (запутанные) состояния не имеют никакого аналога в классической физике. Они никак не могут быть ею объяснены и описаны. Вообще же чистых сепарабельных состояний вокруг нас нет — все когда-то образовалось, вероятно, из единого источника, однако методами квантовой теории можно описывать неотделимые состояния как отделимые, пренебрегая запутанностью, обнуляя недиагональные элементы в матрице плотности. Так и получается классическая физика.

Полная несепарабельность — это максимальная запутанность с окружением по всем степеням свободы, что означает полную нелокальность объекта. Если объекты локализованы, значит, по каким-то степеням свободы мы можем записать сепарабельный вектор состояния (диагональную матрицу плотности), взяв в качестве базисных векторов сепарабельные собственные состояния. Например, запутанную по спинам пару частиц можно описать двумя различными векторами состояния: один вектор — в координатном представлении — тогда частицы будут сепарабельны по координатам, и с каждой частицей сопоставляется свой вектор состояния (тоже в координатном базисе). С другой стороны, мы можем записать вектор состояния этой пары частиц в спиновом представлении, в базисе по спиновым степеням свободы. Тогда система будет несепарабельна по этим степеням свободы, и мы уже не сможем записать свои векторы состояния для каждой частицы в этом базисе.

Когда квантовая теория обогатилась пониманием того, что квантовая запутанность — это обычная физическая величина, и с ней можно работать, как с другими физическими величинами, такими как энергия, масса и т. д., то возникла необходимость в ее количественном описании. Запутанные состояния нужно было охарактеризовать по величине (степени) запутанности. Одним из первых такую количественную характеристику, то есть меру запутанности, ввел в 1996 году Чарльз Беннетт с соавторами.

В зависимости от величины квантовой запутанности (она изменяется от нуля до единицы) система может состоять из отделимых локальных частей, которые слабо связаны друг с другом. В этом случае мера запутанности близка к нулю. Если же система составляет единое неразделимое целое, то мера запутанности равна единице. Это нелокальное состояние, и тогда в системе нет никаких классических, «видимых» объектов.

Разделить на строго независимые части можно систему, части которой находятся в сепарабельном (незапутанном) состоянии (мера запутанности равна нулю). Такое разделение возможно только в том случае, если части системы никогда не взаимодействовали друг с другом.

Вообще любой объект, который взаимодействует со своим окружением, находится с ним в запутанном состоянии. Величина запутанности зависит от интенсивности взаимодействия. Так, управляя взаимодействием с окружением, можно манипулировать мерой квантовой запутанности между составными частями системы. Например, замкнутая система может находиться в максимально запутанном состоянии и не будет иметь внутри себя локальных (классических) составных частей (подсистем). Но если она начинает взаимодействовать с окружением, то мера запутанности между ее подсистемами постепенно уменьшается, и они «проявляются» в виде локальных объектов. При наличии взаимодействия с окружением суперпозиция разрушается, и проявляется то или иное локальное состояние в зависимости от типа взаимодействий. Этот физический процесс называется декогеренцией. Догеренция – это процесс перехода чистого состояния в смешанное. Другой стороной этого процесса является возрастание меры запутанности системы с окружением. Оно будто «растаскивает» в разные стороны части того, что раньше было единым целым, придает им определенную форму, и они становятся видимыми, различимыми с нашей привычной, классической точки зрения.

Именно процесс догеренции создает много сложностей при разработке квантового компьютера, поскольку нарушает когерентную согласованную работу кубитов. Вследствие декогеренции вместо внутренней запутанности между кубитами, которой компьютер может управлять и которая полностью ему подвластна, возникает запутанность с окружением. Работать с ней квантовый компьютер не в состоянии

Существует и обратный процесс - запутанность можно «концентрировать», увеличивать. Этот процесс называется рекогеренцией.

Декогеренция и рекогеренция — самые фундаментальные физические процессы в окружающей реальности, известные науке к настоящему времени. Процесс декогеренции лежит в основе всех известных классических взаимодействий (гравитационного, электромагнитного и т. д.), которые можно считать лишь его следствием. Различные виды взаимодействий в этом плане рассматриваются как отдельные каналы декогеренции. Взаимодействия могут быть любые — все, которые сопровождаются изменением состояния системы.

В физических экспериментах можно изучать различные типы взаимодействий непосредственно в аспекте декогеренции. Это, например, делалось в экспериментах А. Цайлингера (Nature 427, 711–714 (2004), где исследовался процесс декогеренции по одному из каналов взаимодействия с окружением — за счет теплового излучения. Эти процессы фундаментальные, и характерны они не только для микрочастиц, а для любых объектов, в том числе и для макроскопических тел. Декогеренция тепловым излучением — общий механизм, который относится ко всем макроскопическим телам. По большому счету, все взаимодействия являются «эффектом декогеренции». Более того, согласно теории декогеренции, весь классический мир — это «эффект декогеренции».

Мера квантовой запутанности непосредственно связана с информацией, содержащейся в системе, которая может быть выражена количественно, например, через энтропию фон Неймана для чистых состояний.

Проиллюстрируем на простом примере процесс "приготовления" запутанных состояний, рис. 1.2. Рассмотрим источник, испускающий пары частиц так, что одна из них 1 летит налево, а другая 2 - направо. Потребуем, чтобы сохранялась сумма импульсов частиц. Введем дополнительную параметризацию. Каждая частица может полететь и вверх - состояние , и вниз – состояние). Т.к. сумма импульсов сохраняется, то, если первая частица полетела налево вниз, то вторая полетит направо вверх или наоборот, - если первая частица полетела налево вверх, то вторая вынуждена полететь направо вниз.

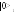
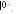
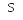
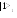
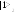
Рис. 1.2. Иллюстрация «приготовления» перепутанных состояний

Полное состояние, которое «приготавливает» источник, записывается в виде суперпозиции двух “возможностей”:

(1.1)

Коэффициенты с_i (i = 1, 2) - это (комплексные) амплитуды двух исходов. Физический смысл состоит в том, что соответствующие квадраты модулей определяют вероятности обнаружить пару частиц в состояниях(первая – вверх, вторая – вниз), либо(вторая – вверх, первая – вниз). Состояние (1.1) -пример перепутанного состояния двух частиц Другие примеры - ионы в ловушках, ядерные спины в молекуле при электронном парамагнитном резонансе, состояния системы «атом-поле» в резонаторе и др.

Перепутанными считаются состояния составной системы, которые не могут быть представлены в виде произведения волновых функций, описывающих ее части по отдельности.

Перепутанные состояния характеризуются следующими атрибутами:

• наличие параметра, принимающего ряд фиксированных значений для каждой из подсистем;

• наличие корреляций между двумя подсистемами по этому параметру, или в более общем случае - синхронности флуктуаций этого параметра;

Другое определение перепутанных состояний для двух подсистем: перепутанными называются две подсистемы, между которыми существуют квантовые корреляции по параметру, принимающему, по крайней мере, два значения для каждой из подсистем. Измерение состояния одной из подсистем однозначно определяет (проецирует) состояние другой. Совместное состояние двух подсистем тогда называется перепутанным. Корреляции должны носить квантовый характер, т.е. их нельзя описать классически. В противном (классическом) случае даже полные (т.е. 100%-ые) корреляции не дают результатов, к которым ведет использование истинных перепутанных состояний.