ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.08.2024
Просмотров: 218
Скачиваний: 0
СОДЕРЖАНИЕ
Травин г.М., Токарев в.А., Родионова е.А.
Содержание Лекция 1. Декомпозиция технологических систем 5
Лекция 1. Декомпозиция технологических систем
1.3. Технологические системы и их элементы
1.4. Состояния и события технической системы
2.3. Показатели оценки надежности
3.1. Факторы и процессы влияния
3.3. Влияние скорости процессов на надежность технических систем
4.2. Характеристика потока отказов
5.1. Вероятность безотказной работы
5.2. Наработка на отказ, до отказа, интенсивность и параметр потока отказов
5.3. Законы распределения времени между отказами
6.1. Понятие физической и моральной долговечности
6.2. Технико-экономическая долговечность
6.3. Определение оптимального срока службы оборудования
6.4. Количественные показатели долговечности
6.5. Выбор показателей долговечности средств технологического оснащения и их элементов
Лекция 7. Ремонтопригодность. Свойства и показатели оценки
7.1. Понятие и свойства ремонтопригодности
7.2. Характеристики свойств ремонтопригодности
7.3. Частные показатели оценки ремонтопригодности
8.1. Требования к информации о надежности
8.2. Методы исследования и оценки надежности
8.3. Комплексные показатели надежности
9.1. Избыточность как основной метод повышения надежности систем
9.3. Методы резервирования элементов
9.4. Методы резервирования систем
9.5. Использование алгебры логики для моделирования систем с резервированием
10.1. Расчет надежности резьбовых соединений
10.2. Расчет надежности сварных соединений
10.3. Расчет надежности соединений с натягом
11.1. Понятие и свойства надежности оперативного персонала
11.2. Виды и формы отказов персонала
9.3. Методы резервирования элементов
Резервирование элементов используется в тех случаях, когда необходимо создавать высоконадежные системы из малонадежных элементов. Различают методы нагруженного и ненагруженного резервирования. Ненагруженное резервирование или резервирование замещением осуществляется путем включения резервного элемента при отказе в системе основного. До отказа это включение невозможно. Схема резервирования приведена на рисунке 14.
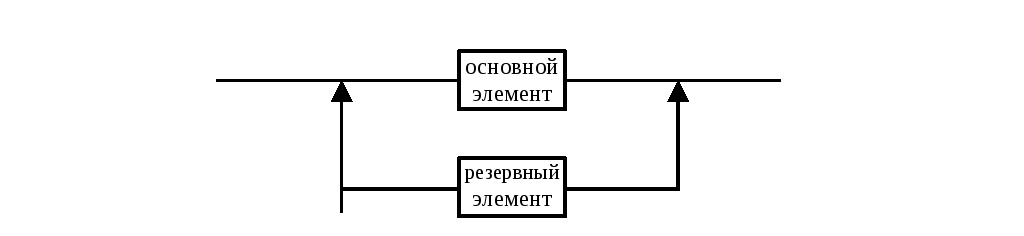
Рисунок 14. Ненагруженное резервирование (замещением)
Вероятность безотказной работы системы
в этом случае рассчитывается
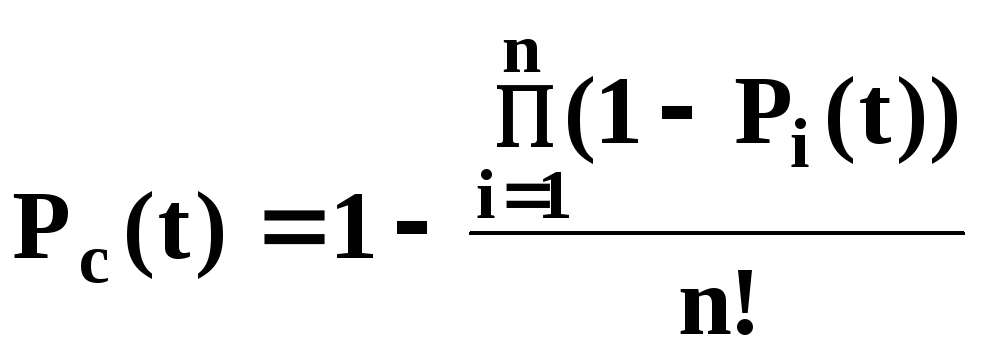 .
.
Замещение отказавшего элемента осуществляется в два этапа:
обнаружение отказавшего элемента органолептическими способами или с помощью специального прибора (устройства);
включение резервного в ручном режиме или с помощью автоматического устройства.
Нагруженное резервирование реализуется в двух вариантах:
резервный элемент работает в одинаковом режиме с основным;
резервный элемент работает в облегченном режиме.
Структурная модель такого резервирования представлена на рисунке 15.
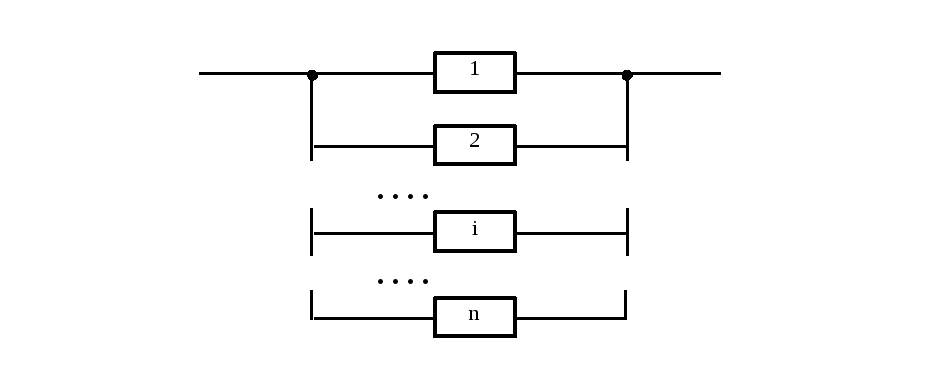
Рисунок 15. Структурная модель нагруженного резервирования
Всего элементов включая резервный – n.
Для случая работы резервных элементов в одном режиме с основным вероятность безотказной работы системы Рс(t) рассчитывается:
![]() ;
;![]()
![]() ,
тогда
,
тогда![]() .
.
При равной надежности элементов
![]() .
.
Дублирование с восстановлением предполагает, что при отказе основного элемента его заменяет резервный. Основной после восстановления работоспособности становится в резерв. На одном из таких циклов может возникнуть ситуация, когда произойдет отказ элемента, а ранее отказавший еще не восстановлен. В этом случае вероятность безотказной работы системы при экспоненциальном законе распределения времени безотказной работы рассчитывается:
![]() ;
;![]() ,
,
где
![]() и
и![]() ‑ интенсивность отказов соответственно
основного и резервного элементов,
‑ интенсивность отказов соответственно
основного и резервного элементов,
![]() ‑ вероятность отказа пары на одном
из циклов.
‑ вероятность отказа пары на одном
из циклов.
![]()
![]() .
.
Закон распределения Рс(t) зависит не от закона распределения времени восстановления работоспособности (устранения отказов) G(t), а только от среднего времени ремонта М(τр) – математического ожидания времени восстановления.
9.4. Методы резервирования систем
Резервирование систем предполагает резервирование всех входящих в систему элементов. Различают: общее резервирование, раздельное и смешанное (комбинированное) резервирование.
Общее резервирование имеет место, когда при отказе любого из элементов основной системы последняя заменяется резервной. Структурная схема общего резервирования представлена на рисунке 16.
Число элементов в системе – n, число резервных цепей m-1, общее число систем – m.
Вероятность безотказной работы системы при общем резервировании
![]() .
.
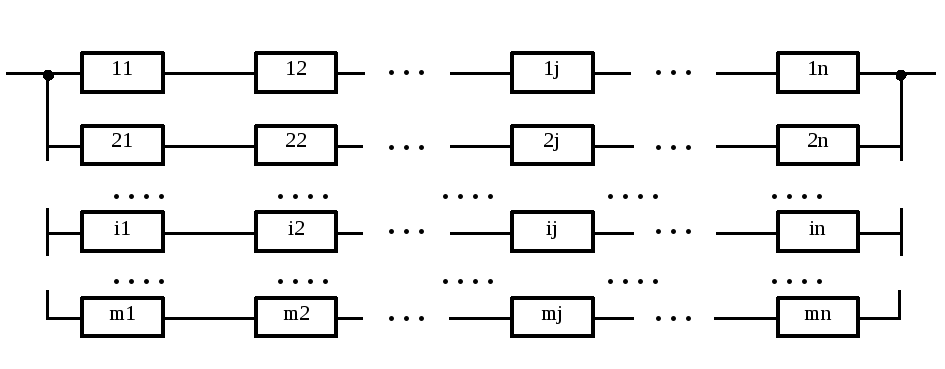
Рисунок 16. Модель общего резервирования
![]()
При равной безотказности элементов упрощенное выражение для расчета общей безотказности системы
![]() .
.
При раздельном резервировании избыточность создается за счет резервирования каждого элемента системы в отдельности. Структурная схема раздельного резервирования отражена на рисунке 17.
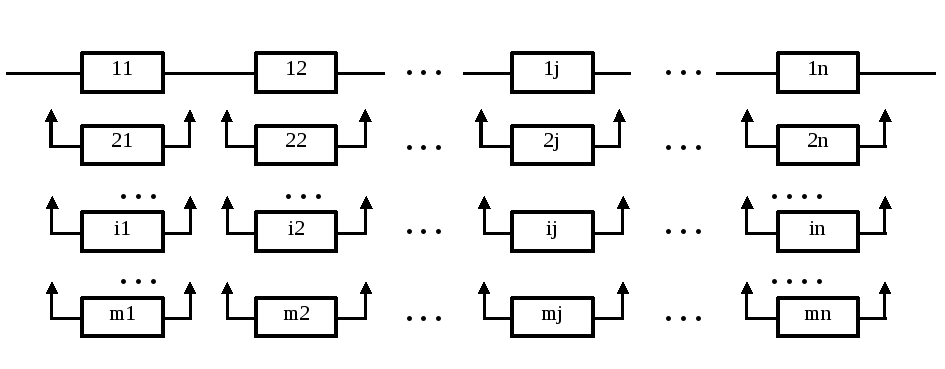
Рисунок 17. Модель раздельного резервирования
Вероятность безотказной работы системы с раздельным резервированием элементов
![]() .
.
При равной безотказности элементов
![]() .
.
Проанализируем эффективность как общего, так и раздельного резервирования. Пусть Pij(t)=0,9;n=4; m=3.
При общем резервировании
![]() .
.
При раздельном резервировании
![]() .
.
Как видно, раздельное резервирование более эффективно, чем общее. Однако технически его гораздо сложнее осуществить.
Комбинированное (смешанное) резервирование, т.е. сочетание общего и раздельного, применяется тогда, когда необходимо в большей степени повысить надежность некоторых элементов. В этом случае именно эти элементы резервируются раздельно, а все остальные элементы системы по схеме общего резервирования.
9.5. Использование алгебры логики для моделирования систем с резервированием
Для сложных технических систем структурные модели надежности с целью упрощения преобразуются в логические модели, построенные на основе алгебры логики или булевой алгебры (с использованием аппарата алгебры логики).
Безотказная работа объекта (событие) обозначается буквами латинского алфавита – А, альтернативное событие – отказ обозначается Ā (читается «не А»). При графическом изображении эти же события соответственно обозначаются А, А.
Л не
или
и
Рассмотрим на примере, представленном структурной схемой на рисунке 19, использование данного аппарата.
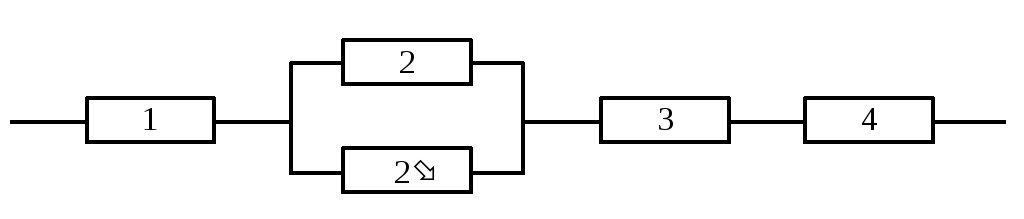
Рисунок 19. Исходная структурная схема
Построим аналитическую модель всех вариантов безотказной работы данной системы в символах алгебры логики. Безотказная работа системы (В):
В=(А1А2![]() А3А4)(А1
А3А4)(А1![]() Ошибка!
Ошибка связи.А3А4)(А1А2
Ошибка!
Ошибка связи.А3А4)(А1А2![]() А3А4)
А3А4)
Логическая модель записывается так, как «логично» читается: система работает безотказно если исправны элемент А1и А2и А2и А3и А4, или исправен А1, отказал А2и исправен А2и А3и А4, или исправен А1и А2и отказал А2и исправны А3и А4.
Преобразуем модель в символах теории
вероятностей при Р2=![]() :
:
Рс(t)=Р1·Р2·![]() ·Р3·Р4+Р1·(1–Р2)·
·Р3·Р4+Р1·(1–Р2)·![]() ·Р3·Р4+Р1·Р2·(1–
·Р3·Р4+Р1·Р2·(1–![]() )·Р3·Р4=
)·Р3·Р4=
=Р1·Р2·Р3·Р4(Р2+(1–Р2)+(1-Р2)=Р1·Р2·Р3·Р4(2–Р2)
Построим графическую логическую модель безотказности системы (рисунок 20).
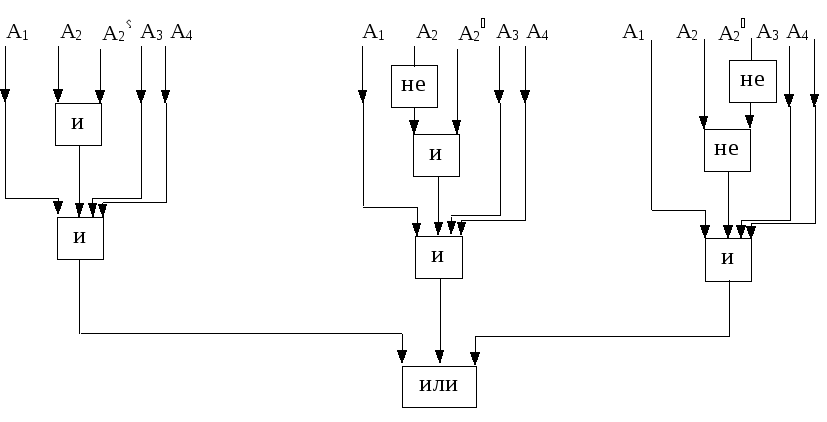 Рисунок
20. Графическая логическая модель
безотказности системы
Рисунок
20. Графическая логическая модель
безотказности системы
Вопросы для самоконтроля
Каким образом в повышении надежности используется принцип избыточности?
Как соотносятся конструктивное соединение элементов системы и структурные схемы надежности?
В чем суть и цель резервирования элементов?
Если в двигателе внутреннего сгорания предусмотрено 4 цилиндра, можно ли утверждать об использовании в этом случае резервирования?
Чем отличается резервирование замещением от резервирования дублированием с восстановлением?
Что эффективнее: общее резервирование системы или раздельное? Какое из них сложнее в реализации?
В чем особенность записи при составлении аналитических логических моделей надежности систем с резервированием?
«Представляется, что для нашей эпохи характерны совершенство средств и путаница целей»
Альберт Эйнштейн
Лекция 10. Методы расчета соединений деталей на надежность
|
10.1. Расчет надежности резьбовых соединений 10.2. Расчет надежности сварных соединений 10.3. Расчет надежности соединений с натягом |
Нераскрытие стыка, несдвигаемость стыка, статическая прочность, сопротивление усталости, затяжка резьбы, предел выносливости, коэффициент трения, концентрация напряжений, ручная, автоматическая сварка, стыковая сварка, сварка внахлестку, в тавр, эквивалентное напряжение, соединение с натягом, модуль упругости, коэффициент поперечного сжатия |
10.1. Расчет надежности резьбовых соединений
Вероятность безотказной работы резьбового соединения рассчитывается как произведение вероятностей безотказной работы по четырем основным критериям:
Pрез=P1·P2·P3·P4,