Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx

8. Определение выброса в данных. Приведите примеры конвенций для определения верхней и нижней границы нормальных значений данных. Через IQR или sigma

К оглавлению

Мы уже несколько раз упоминали «экстремальные» или «аномальные» значения в распределениях. Например, когда говорили, как сильно зависят от таких значений среднее распределения или его размах. Теперь, когда мы поговорили о z-оценках, мы можем ввести понятие выброса.

Выброс — это аномальное значение в данных, которое значительно отличается от значения, выраженного мерой центральной тенденции.

Например, предположим, что приемная комиссия собирает статистику о заработной плате выпускников определенных факультетов для рекламной кампании. Если 4 выпускника получают 35, 47, 50 и 68 тысяч рублей в месяц, а их одногруппник — 250, то мы явно можем сказать, что это значение нетипично для нашей выборки. Но было бы здорово эту «нетипичность» формализировать. Определение выбросов обычно субъективно, но есть некоторые конвенции. Например, значения отличающиеся от среднего на 3 и больше среднеквадратичных отклонений называют сильными выбросами, а от 2 до 3 отклонений – умеренными. Давайте посмотрим, каким выбросом является зарплата нашего «нетипичного» выпускника. Сначала найдем z-оценку для X=250:

X=250,M=90,s=80.69

z=(250−90)/80.69=1.98

Можно говорить, что зарплата в 250 тысяч рублей для нашей выборки действительно является умеренным выбросом. Мы можем выразить выбросы и через квартили. Например, в популярном виде визуализации «ящик-с-усами», на котором можно увидеть медиану и интерквартильный размах, обычно отображаются и выбросы — все что вышло за границы «усов». Эти границы обычно рассчитываются так:

Нижняя граница=Q1−1.5IQR

Верхняя граница=Q3+1.5IQR

Еще раз обратим внимание, что эти определения — конвенции, договоренности между специалистами. И в разных сферах они могут отличаться. Поэтому когда вы работаете с результатами чужого анализа или строите графики в новом для вас программном обеспечении — узнайте, как определяются выбросы, чтобы избежать сюрпризов.

Зачем находить выбросы? Во-первых, так как эти значения аномальны, они могут нести в себе какую-то интересную информацию. Например, в том же примере с зарплатами имеет смысл посмотреть, а какими такими квалификациями обладает этот выпускник? Может он параллельно окончил второе высшее по более оплачиваемой специальности. Или же он просто попал на очень редкую вакансию по специальности, которая высоко оплачивается. В первом случае такое наблюдение для наших задач нерелевантно, а во втором, наоборот, становится интересным кейсом, про который можно рассказать абитуриентам. Во-вторых, как мы уже видели, выбросы могут повлиять на расчеты некоторых метрик. Если значения выбросов действительно нетипичны и обусловлены какими-то понятными причинами нерелевантными вашему исследовательскому вопросу, то от таких наблюдений можно избавиться. Другой стратегией будет смягчение влияния

---

выбросов с помощью специальных приемов, но этот вопрос выходит за рамки нашего курса.
9. Стратегии работы с пропущенными значениями в данных. Приведите примеры действий для разных данных (заполнение средним значением, медианой, использование вектора значений, удаление столбцов с данными)
К оглавлению

Реальные наборы данных могут быть неполными. Не в том смысле, что в анализ не вошли какие-то важные точки или неудачно были выбраны параметры, а просто отсутствуют некоторые данные, которые в принципе должны были там быть.

Это может случиться из-за технических проблем, или если датасет собран из нескольких источников с разными наборами параметров; важно то, что в таблице присутствуют пустые ячейки. Вместо значений в них ставится какая-нибудь заглушка — NaN, просто пустая ячейка или ещё что-нибудь в этом роде. Если их много — тренировка на таких данных сильно ухудшит качество модели, а то и окажется вовсе невозможной. Многие алгоритмы того же scikit-learn не только требуют массив чисел (а не NaN или «missing»), но и ожидают, что этот массив будет состоять из валидных данных.

Что делать? Можно, конечно, просто выкинуть все неполные наблюдения, но так можно потерять ценную информацию. Лучше попытаться восстановить недостающие значения на основании остальных данных в наборе, или хотя бы вставить в пустые ячейки что-нибудь более-менее осмысленное. Этот процесс называется импутацией данных.

Способ первый: не делать ничего

Тут всё просто: отдаём алгоритму датасет в исходном виде и надеемся, что он с ним как-нибудь разберётся. Некоторые алгоритмы умеют принимать во внимание и даже восстанавливать пропущенные значения в данных. Например, XGBoost делает это за счёт уменьшения функции потерь при обучении. У алгоритма может быть параметр, позволяющий их проигнорировать (пример — LightGBM с параметром use_missing=False). Но таких опций может и не быть: линейная регрессия в scikit-learn просто объявит массив некорректным и выбросит исключение. Так что в её случае (как и в случае многих других алгоритмов) готовить данные к анализу всё-таки придётся пользователю.

Плюсы:

Не надо думать об алгоритмах импутации — выставил соответствующие параметры и всё работает.

---

Минусы

Нужно понимать, как именно алгоритм обойдётся с недостающими данными. В противном случае есть риск получить какие-нибудь артефакты и даже не узнать, какие именно.

Способ второй: импутация данных средним/медианой

Тоже не особенно сложно: считаем среднее или медиану имеющихся значений для каждого столбца в таблице и вставляем то, что получилось, в пустые ячейки. Естественно, этот метод работает только с численными данными.







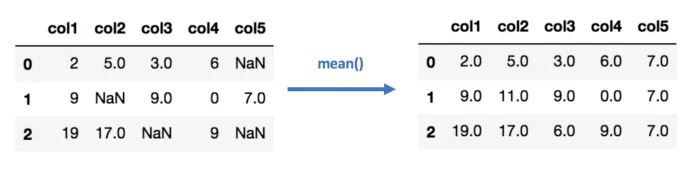
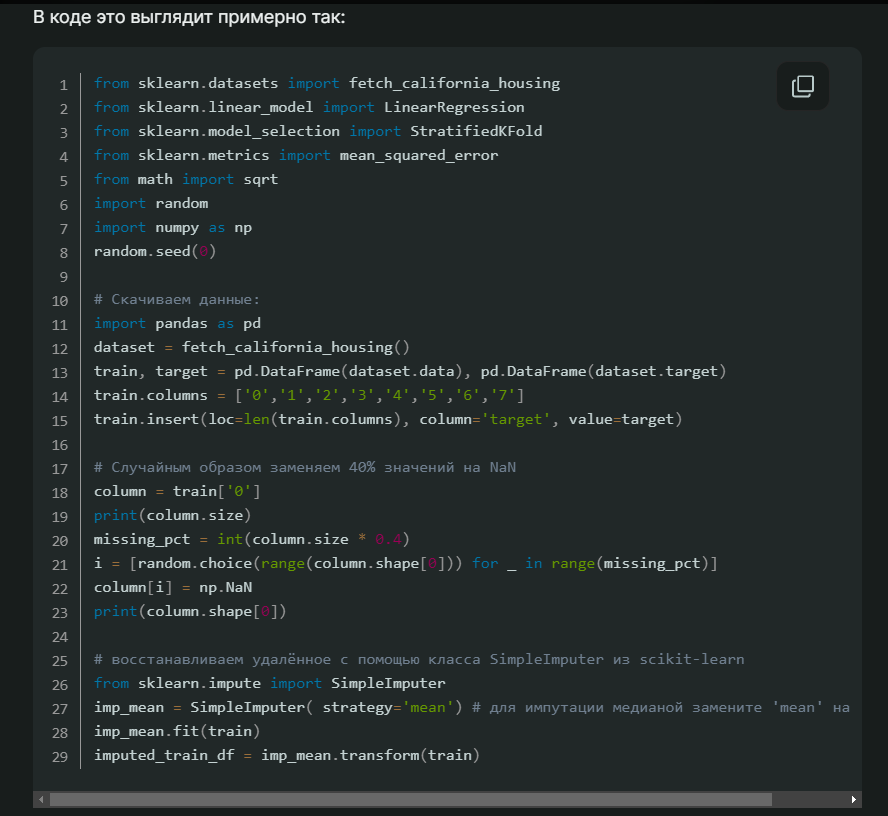
Плюсы:

• 
  Просто и быстро.
  
• 
  Хорошо работает на небольших наборах численных данных.
  

Минусы:

• 
  Значения вычисляются независимо для каждого столбца, так что корреляции между параметрами не учитываются.
  
• 
  Не работает с качественными переменными.
  
• 
  Метод не особенно точный.
  
• 
  Никак не оценивается погрешность импутации.
  

Способ третий: импутация данных самым частым значением или константой

Импутация самым часто встречающимся значением — ещё одна простая стратегия для компенсации пропущенных значений, не учитывающая корреляций между параметрами. Плюсы и минусы те же, что и в предыдущем пункте, но этот метод предназначен для качественных переменных.



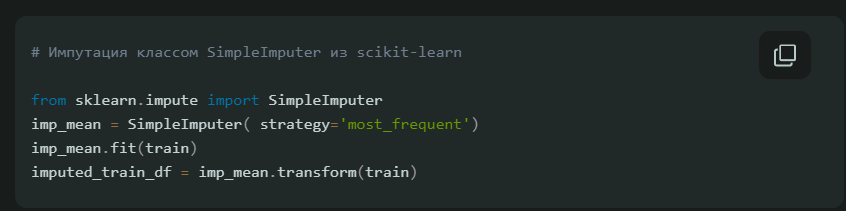
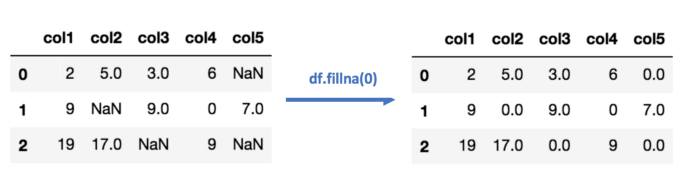
В случае импутации нулём или константой (как можно догадаться из названия) все пропущенные значения в данных заменяются определённым значением.



Способ четвёртый: импутация данных с помощью k-NN

k-Nearest Neighbour (k ближайших соседей) — простой алгоритм классификации, который можно модифицировать для импутации недостающих значений. Он использует сходство точек, чтобы предсказать недостающие значения на основании k ближайших точек, у которых это значение есть. Иными словами, выбирается k точек, которые больше всего похожи на рассматриваемую, и уже на их основании выбирается значение для пустой ячейки. Это можно сделать с помощью библиотеки Impyute:

---

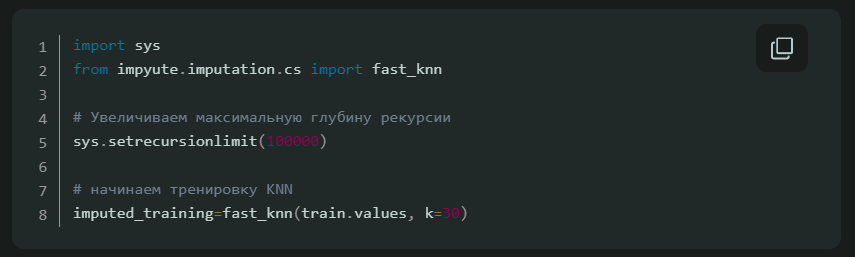
Алгоритм сперва проводит импутацию простым средним, потом на основании получившегося набора данных строит дерево и использует его для поиска ближайших соседей. Взвешенное среднее их значений и вставляется в исходный набор данных вместо недостающего.

Плюсы:

• 
  На некоторых датасетах может быть точнее среднего/медианы или константы.
  
• 
  Учитывает корреляцию между параметрами.
  

Минусы:

• 
  Вычислительно дороже, так как требует держать весь набор данных в памяти.
  
• 
  Важно понимать, какая метрика дистанции используется для поиска соседей. Имплементация в impyute поддерживает только манхэттенскую и евклидову дистанцию, так что анализ соотношений (скажем, количества входов на сайты людей разных возрастов) может потребовать предварительной нормализации.
  
• 
  Чувствителен к выбросам в данных (в отличие от SVM).
  

Способ пятый: импутация данных с помощью MICE



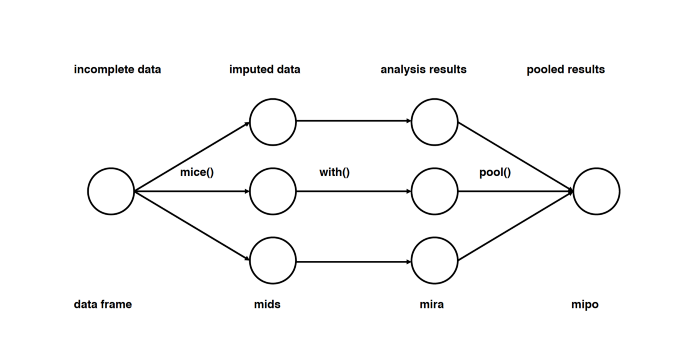
Этот подход основан на том, что импутация каждого значения проводится не один раз, а много. Множественные импутации, в отличие от однократных, позволяют понять, насколько надёжно или ненадёжно предложенное значение. Кроме того, MICE позволяет работать с переменными разных типов (например двоичными и количественными), а также со сложными штуками вроде предельных значений и паттернов артефактов в исходных данных. Подробный разбор математики есть в оригинальной статье.

Метод MICE подразумевает не просто множественные импутации, а многократное повторение дальнейшего анализа на разных импутированных наборах данных и интеграцию получившихся результатов.

Способ шестой: импутация данных с помощью глубокого обучения

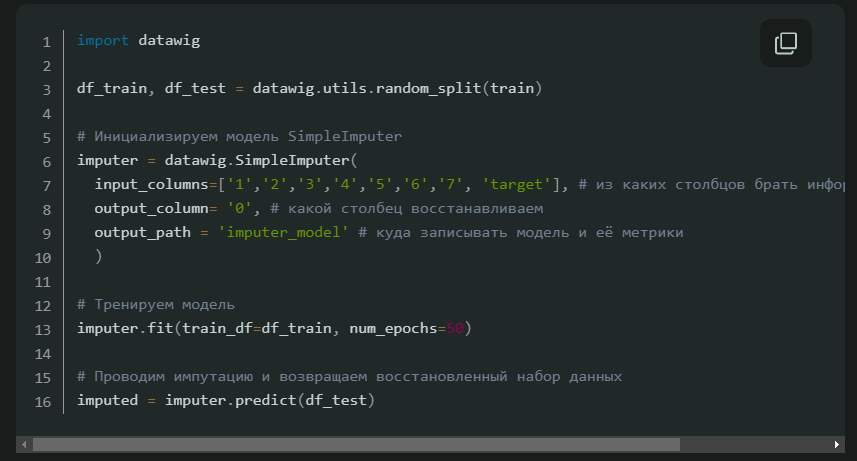
Показано, что глубокое обучение хорошо работает с дискретными и другими не-численными значениями. Библиотека datawig позволяет восстанавливать недостающие значения за счёт тренировки нейросети на тех точках, для которых есть все параметры. Поддерживается тренировка на CPU и GPU.



Плюсы:

• 
  Точнее других методов.
  
• 
  Может работать с качественными параметрами.
  
• 
  Поддерживает CPU и GPU.
  

---

Минусы:

• 
  Восстанавливает только один столбец.
  
• 
  На больших наборах данных может быть вычислительно дорого.
  
• 
  Нужно заранее решить, какие столбцы будут использоваться для предсказания недостающего значения.
  

Другие методы импутации данных

Стохастическая регрессия

Примерно похоже на регрессионную импутацию, в которой значения восстанавливаются регрессией от имеющихся значений для той же точки, но добавляет случайный шум.

Экстраполяция и интерполяция

Пытается восстановить значения на основании ограниченного набора известных точек.

Hot-deck

Значение берётся из другой точки, похожей по имеющимся параметрам на восстанавливаемую. Грубо говоря, это похоже на k-NN, но используется только один «сосед».

Как мы видим, универсального метода импутации не существует. Одни стратегии работают лучше на одних наборах данных или типах недостающих переменных, другие на других. Если не считать очевидных правил насчёт типов данных (например, у качественных переменных просто не может быть среднего), то можно только посоветовать экспериментировать и смотреть, какой метод сработает лучше на данном конкретном датасете.

---