Файл: Учебное пособие Томск 2001 удк.doc

если ₁и ₂ соизмеримы.

Теплопередача через многослойную цилиндрическую стенку рассчитывается по формуле

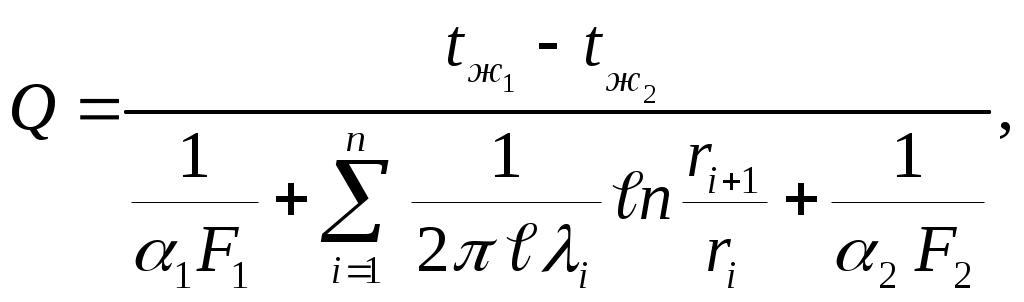(2.35)

где F₁и F₂ – площади внутренней и наружной поверхностей многослойной цилиндрической стенки.

---

2.4. Критический диаметр тепловой изоляции

Тепловой изоляцией является покрытие из теплоизоляционного материала, которое способствует снижению потерь в окружающую среду.

Пусть труба покрыта слоем тепловой изоляции (рис. 2.7, а).





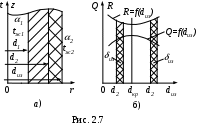
Теплопотери (Q, Вт) через теплоизолированную стенку трубы можно представить формулой

(2.36)

где

(2.37)

Графическая зависимость R=f(d_из) представлена на рис. 2.7, б, откуда следует, что термическое сопротивление изоляции с увеличением диаметра изоляции может уменьшаться до минимального значения, а затем увеличиваться. Так как теплопотери (Q) обратно пропорциональны термическому сопротивлению (R) согласно (2.36), то зависимость Q=f(d_из) является зеркальным отображением кривой R=f(d_из).

Значение d_из , соответствующее минимуму кривой R=f(d_из), называется критическим диаметром d_кр и может быть определено из условия минимума функции

(2.38)

Совместное решение (2.38) и (2.37) дает



откуда

(2.39)

Критическому диаметру изоляции соответствует минимальное термическое сопротивление и максимальный тепловой поток.

Анализ уравнения (2.37) показывает:

а) при наложении тепловой изоляции толщиной δ_из на трубу с d_2кр (рис. 2.7, б) термическое сопротивление уменьшается, теплопотери увеличиваются, т.к. увеличивается площадь теплоотдающей поверхности изоляции
(π d_из );

б) если d₂>d_кр , термическое сопротивление увеличивается, теплопотери уменьшаются, тепловая изоляция оправдывает свое назначение, т.к. третье слагаемое в уравнении (2.37) становится существенно больше, чем четвертое.

Таким образом, тепловая изоляция уменьшает теплопотери, если
d₂ d_кр,



откуда

(2.40)

Правильно подобранный теплоизоляционный материал должен удовлетворять условию (2.40).

Контрольные вопросы и задания

1. 
   Как изменяется термическое сопротивление плоской стенки: а) с увеличением толщины стенки (δ); б) с увеличением коэффициента теплопроводности (λ)? Сравните термическое сопротивление пластин одинаковой толщины из текстолита и стали.
   
2. 
   Как рассчитать передаваемую теплоту через плоскую стенку за одни сутки, если известны температуры на поверхностях стенки (t₁и t₂), толщина стенки (δ), коэффициент теплопроводности (λ), площадь изотермической поверхности (F)?
   
3. 
   Рассчитайте эффективный коэффициент теплопроводности (λ_эф) для конденсатора, набранного из 7 дюралевых листов толщиной δ₁=1,5мм с теплопроводностью λ₁=174 Вт/м· К, между которыми находится пропиточная бумага с толщиной слоев δ₂=3мм, λ₂=0,116 Вт/м· К. Ответ: λ_эф=0,184 Вт/м· К.
   
4. 
   Тепловой поток, передаваемый теплопроводностью через цилиндрическую или плоскую стенку, рассчитывается по формуле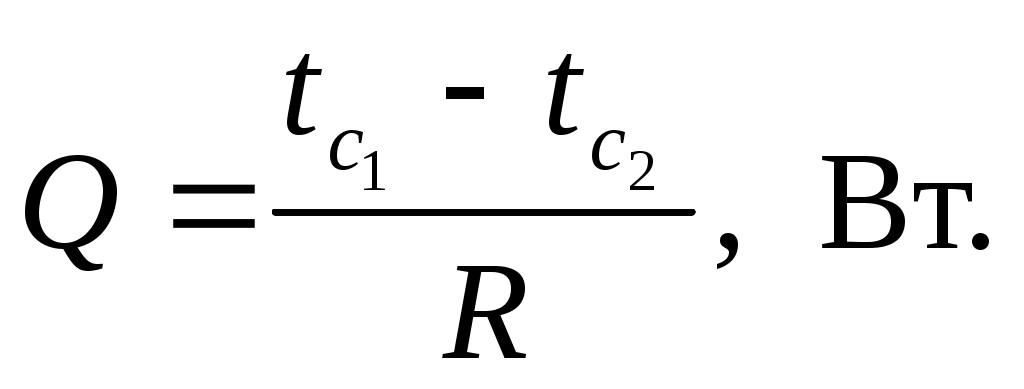 Запишите формулы для термического сопротивления (R) плоской и цилиндрической стенок.
   
5. 
   Температура внутренней поверхности цементной трубы t₁=50^oC, наружной – t₂=-20^oC. Запишите уравнение, по которому можно рассчитать радиус изотермической поверхности с температурой t=0^оС.
   
6. 
   Что можно сказать о температурах среды (t_ж) и поверхности стенки (t_с) при условии ?
   
7. 
   Запишите формулу для коэффициента теплопередачи многослойной плоской стенки.
   
8. 
   Запишите термическое сопротивление теплопроводности и термическое сопротивление теплоотдачи цилиндрической стенки. Какие перепады температур они определяют?
   
9. 
   Наложение электроизоляции на кабели и провода с d_2кр улучшает их охлаждение, снижает температуру. При каком диаметре изоляции охлаждение будет максимальным, а температура минимальной? Какому условию по λ_из должен удовлетворять правильно подобранный электроизоляционный материал?
   

Задачи для самостоятельного решения

Задача № 1. Стены сушильной камеры выполнены из красного кирпича толщиной δ₁=250мм с коэффициентом теплопроводности λ₁=0,7 Вт/м· К и слоя строительного войлока с коэффициентом теплопроводности
λ₂=0,0405 Вт/м ·К. Температура наружной поверхности кирпичного слоя t₁=110^oC, наружной поверхности войлочного слоя t₃=25^oC.

Определить температуру плоскости соприкосновения слоев t₂ и толщину войлочного слоя δ₂ при условии, что тепловые потери камеры не превышают q=110 Вт/м².

Каков эффективный (средний) коэффициент теплопроводности двухслойной стенки?

Примечание. Расчетные формулы для решения данной задачи содержатся в разделе 2.1 настоящего пособия.

Ответы: t₂=70,7^оС; δ₂=16,8мм; λ_эф=0,326 Вт/ м · К.
Задача № 2. Паропровод диаметром d₂ / d₁ =160/150 мм покрыт слоем тепловой изоляции толщиной δ=100 мм; коэффициент теплопроводности стенки трубы λ₁=50 Вт/ м· К, изоляции λ₂=0,08 Вт/м· К. Температура внутренней поверхности трубопровода t₁=400^оС, наружной поверхности изоляции t₃=50^оС.

Найти тепловые потери на 1 м длины паропровода (Q , Вт/м) и перепады температур на трубе (t₁- t₂) и на слое изоляции (t₂- t₃).

Примечание. Расчетные формулы содержатся в разделе 2.2.

Ответы: Q =216,8 Вт/м; t₁- t₂=0,045^оС; t₂- t₃=349,95^оС.
Задача № 3. Определить потерю теплоты с 1 м длины трубопровода
(Q , Вт/м) диаметром d₂ / d₁ =165/150 мм, покрытого слоем изоляции толщиной δ=60 мм. Коэффициент теплопроводности трубы λ₁=50 Вт/м· К, изоляции λ₂=0,15 Вт/м ·К. Температура воды в трубопроводе коэффициент теплоотдачи от воды к стенке трубы =1000 Вт/ (м²· К), температура окружающего воздуха коэффициент теплоотдачи от поверхности изоляции к воздуху =8 Вт/ м²· К.

Рассчитать также температуру наружной поверхности изоляции (t_из).

Сравнить Q с потерями теплоты от оголенного трубопровода (Q ΄) при условии одинакового .

Рассчитать потери теплоты от оголенного трубопровода (Q ΄΄) по приближенной формуле (для плоской стенки толщиной ) и определить относительную погрешность расчета

Примечание. Все необходимые расчетные формулы содержатся в разделе 2.3.

Ответы: Q =145,4 Вт/м; t_из=5,3^оС; Q ΄=430,9 Вт/м; Q ΄΄=431,2Вт/м δ=0,07 %.
Задача № 4. Можно ли использовать асбест с коэффициентом теплопроводности λ=0,11 Вт/ м ·К для теплоизоляции трубопровода с d₂=20 мм, если коэффициент теплоотдачи =8 Вт/ м²·К?

Каким должен быть максимальный коэффициент теплопроводности изоляции, используемой для этой цели?

Примечание. Расчетные формулы содержатся в разделе 2.4.

Ответы: Нельзя, т.к. d_2кр=27,5 мм;

1   2   3   4   5   6   7   8   9   10   ...   28

---

3. ТЕПЛОПРОВОДНОСТЬ ТЕЛ
С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛА
ПРИ СТАЦИОНАРНОМ РЕЖИМЕ

Примеры процессов с внутренним тепловыделением: выделение джоулевой теплоты при прохождении электрического тока по проводникам; объемное выделение теплоты в тепловыделяющих элементах ядерных реакторов; выделение теплоты при протекании ряда химических реакций и т.д.

Важной исходной величиной для расчета теплопроводности в телах с внутренними источниками теплоты является плотность объемного тепловыделения



где Q, Вт – теплота, выделяемая за 1с; V, м³ – тепловыделяющий объем.

Для проводников электрического тока выделяемая джоулевая теплота равна электрической мощности (Q=N), а плотность объемного тепловыделения

3.1. Теплопроводность однородной пластины

Симметричные условия охлаждения (граничные условия третьего рода)

Дано: тонкая пластина, толщиной 2 площадью поверхности F, м² с коэффициентом теплопроводности =const, с объемным тепловыделением q_v находится в среде с температурой t_ж=const (рис. 3.1). Задан коэффициент теплоотдачи Условие "тонкой" пластины предполагает пренебрежимо малый отток тепла в среду с торцов, теплота передается в среду только с боковых поверхностей пластины.

О 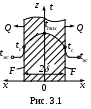пределить: уравнение температурного поля t=f(x), тепловой поток Q, отводимый с боковой поверхности пластины.

Температурное поле пластины описывается дифференциальным уравнением теплопроводности (1.13). Для стационарного режима при отсутствии теплоотдачи с торцов оно запишется в виде

(3.1)

---

Дифференциальное уравнение второго порядка требует два дополнительных условия однозначности для определения констант интегрирования. Такими условиями являются граничное условие третьего рода (заданы t_ж, ), которое на основании (1.15) для данной задачи запишется в виде

(3.2)

и условие максимума температуры в центре пластины

(3.3)

Система уравнений (3.1) – (3.3) является математической постановкой задачи.

Граничные условия на поверхностях пластины одинаковы, тепловые потоки, отводимые с поверхностей, одинаковы поэтому можно рассматривать лишь одну половину пластины, например правую, для которой записано граничное условие (3.2).

После интегрирования (3.1) получим

(3.4)

(3.5)

Уравнение (3.5) - общий интеграл уравнения (3.1). Постоянные интегрирования с₁ и с₂определяются с помощью граничных условий (3.2) и (3.3). Из уравнения (3.4) с учетом (3.3) получим



Из уравнения (3.4) при х= имеем



а из (3.5) при х=



Значения и t_с подставим в (3.2) и найдем постоянную интегрирования

---

После подстановки значений с₁ и с₂ в (3.5) получим уравнение температурного поля t=f(x) при граничных условиях третьего рода

(3.6)

где х – текущая координата.

Уравнение (3.6) – симметричная парабола (рис. 3.1). Максимальная температура (t_тах) – в центре пластины (х=0), минимальная (t_с) – на поверхности пластины (х=). При этих условиях из (3.6) можно получить расчетные формулы для максимальной температуры и температуры поверхности пластины:

	(3.7)
	(3.8)

Если в уравнение (3.6) подставить значение t_с согласно (3.8), то получим уравнение температурного поля пластины t=f(x) при граничных условиях первого рода

(3.9)

Тепловой поток, рассеиваемый поверхностью F, рассчитывается по формулам:

	(3.10)
	(3.11)

где V, м³ - объем пластины.

Суммарный тепловой поток, рассеиваемый двумя боковыми поверхностями, вдвое больше, т.к. площадь поверхности охлаждения F_охл=2F, тепловыделяющий объем - V, м³.
Несимметричные условия охлаждения (граничные условия третьего рода)

Д 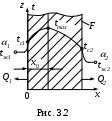ано: тонкая пластина толщиной 

---