Файл: Методические указания по выполнению контрольной работы по учебной дисциплине ен. 02 Элементы математической логики.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 203
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Так как в последнем столбце таблицы все значения истины, следовательно, формула тождественно истина.
3. Равносильные преобразования формул логики высказываний
Пример 1: Дана формула логики высказываний:
С помощью равносильных преобразований выясните, какая эта формула, тождественно истинная, тождественно ложная или только выполнимая.
Решение:
Таким образом, доказано, что данная формула логики тождественно истинная.
Пример 2: Упростите формулу логики высказываний
Решение:
4. Дизъюнктивная и конъюнктивная нормальные формы.
Элементарной конъюнкцией от переменных
Примеры элементарных конъюнкций:
Теорема 1: Элементарная конъюнкция
Дизъюнктивной нормальной формой (ДНФ)
называют формулу логики высказываний, которые представляют собой дизъюнкцию элементарных конъюнкций.
Теорема 2 (критерий ложности): ДНФ тождественно ложна тогда и только тогда, когда в каждую элементарную конъюнкцию входят элементы вида
Замечание: i для каждой элементарной конъюнкции свой
Примеры:
1.
2.
Элементарной дизъюнкцией от переменных
Примеры элементарных дизъюнкций:
Теорема 3: Элементарная дизъюнкция
тождественно истинной тогда и только тогда, когда существуют переменные высказывания
Конъюнктивной нормальной формой (КНФ) называют такую форму логики высказываний, которая представляет собой конъюнкцию элементарных дизъюнкций.
Теорема 4 (критерий истинности): КНФ тождественно истинно тогда и только тогда, когда каждая элементарная дизъюнкция содержит набор переменных
Замечание: i для каждой элементарной дизъюнкции свой.
Примеры:
1.
- КНФ
2.
Две операции конъюнкция и дизъюнкция называются двойственными друг к другу, то есть конъюнкцию можно заменить дизъюнкцией, и наоборот.
Для того чтобы от дизъюнкции перейти к конъюнкции, и наоборот, нужно установить двойное отрицание и одно из них применить вместе с законом де Моргана.
Для того чтобы от ДНФ перейти к КНФ, и наоборот, можно применить законы дистрибутивности.
Пример: Приведите формулу к КНФ и ДНФ:
С помощью равносильных преобразований, используя законы логики
высказываний, получим:
Перейдем от КНФ к ДНФ, используя закон дистрибутивности конъюнкции относительно дизъюнкции идемпотентностии и законы дополнительности:
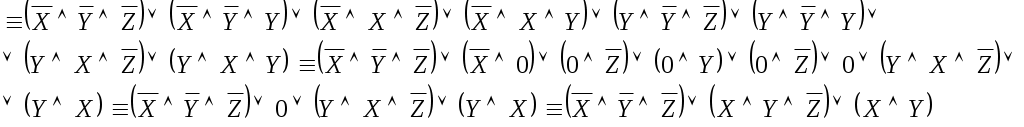 – ДНФ
– ДНФЗамечание: Для того чтобы проверить правильно ли привели формулу к КНФ и ДНФ, можно построить таблицы истинности первоначальной и получившихся формул. Последние столбцы таблиц этих формул должны принимать одинаковые значения истинности.
5. Совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Формула
1) она является ДНФ;
2) каждая элементарная конъюнкция ДНФ содержит все наименования переменных, от которых зависит формула, и каждое наименование входит в него один раз;
3) среди элементарных конъюнкций ДНФ нет одинаковых.
Примеры:
1.
2.
Формула
1) она является КНФ;
2) каждая элементарная дизъюнкция КНФ содержит все наименования переменных, от которых зависит формула и это наименование входит только один раз;
3) среди элементарных дизъюнкций КНФ нет одинаковых.
Пример:
Теорема 1: Если формула не тождественно истинная, то для нее существует и при том единственная СКНФ.
Теорема 2: Если формула не тождественно ложная, то для нее существует и при том единственная СДНФ.
Совершенные формы можно строить с помощью:
1) равносильных преобразований;
2) таблиц истинности.
Алгоритм построения СДНФ с помощью таблице истинности:
Рассмотрим этот алгоритм на конкретном примере, используя таблицу истинности
| X | Y | Z | F(x,y,z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
1) выбираем те строки таблицы , на которых формула принимает значение истина: 2, 4, 7, 8;
2) для каждой выбранной строки строим элементарную конъюнкцию из переменных, от которых зависит формула следующим образом: если переменная в строке принимает значение истина, то она непосредственно входит в элементарную конъюнкцию, если ложь, то она входит с отрицанием;
3) из элементарных конъюнкций составляем ДНФ.
Замечание: Если все строки формулы в таблице истинности принимают значение ложь, то СДНФ построить нельзя.
Алгоритм построения СКНФ
по таблице истинности:
Данный алгоритм аналогичен алгоритму построения СДНФ.
1) выбираем строки таблицы, на которых формула принимает значение ложь: 1, 3, 5, 6;
2) для каждой выбранной строки строим элементарную дизъюнкцию из переменных, от которых зависит формула, следующим образом: если переменная в строке принимает значение ложь, то она сама входит в элементарную дизъюнкцию, если истина, то она входит с отрицанием;
3) из элементарных дизъюнкции составляем КНФ.
Замечание: Если все строки формулы в таблице принимают значение истина, то СКНФ построить нельзя.
С точки зрения алгебры логики представление функции в виде СНКФ рациональнее, когда таблица истинности содержит меньше нулей , чем единиц
Описанный способ нахождения СНДФ и СНКФ исходной формулы по таблице истинности бывает более трудоёмким, чем следующий:
Алгоритм построения СДНФ с помощью равносильных преобразований:
1) приводим исходную формулу к ДНФ;
2) если в элементарную конъюнкцию некоторая переменная входит со своим отрицанием, то удаляем эту конъюнкцию из ДНФ;
3) если в элементарную конъюнкцию некоторая переменная входит несколько раз, то удаляем эти переменные кроме одной;
4) если в некоторую элементарную конъюнкцию некоторая переменная или переменные не входят, то заменяем её на эквивалентную форму, добавляя к ней одну или несколько переменных в виде
5) если в полученной ДНФ имеется несколько одинаковых элементарных конъюнкций, то оставляем только одну из них.
В результате получаем СДНФ.
Пример:
Пусть дана ДНФ функции