Файл: Методические указания по выполнению контрольной работы по учебной дисциплине ен. 02 Элементы математической логики.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 204
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Из таблицы видно, что значения истинности левой и правой частей уравнения совпадают при значениях переменных (0;1) и (1;0). Таким образом, данное уравнение имеет два решения.
3. Решите булево уравнение
Решение: Составим таблицу истинности для левой и правой частей уравнения
| 0 | | | | | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 |
Из таблицы видно, что значения истинности левой и правой частей уравнения совпадают при
АЛГЕБРА ПРЕДИКАТОВ.
1.Основные понятия.
n-местным предикатом (или функцией- высказыванием от n переменных) определённым на множествах
Обозначают n-местный предикат
или,
Высказывание будем считать 0-местным предикатом.
Так как высказывания могут принимать два значения 0- ложь или
-
истина, то и значение предиката может быть либо 0, либо 1.
Примеры:
1. Одноместный предикат, заданный (определённый) на множестве действительных чисел R ,
2. Двухместный предикат, заданный (определённый) на множестве действительных чисел R ,
3. n-местный предикат, заданный (определённый) на множестве действительных чисел R ,
4. n-местный предикат, заданный (определённый) на множестве действительных чисел R ,
Пусть
-
тождественно-истинным, если для любого набора значений аргументов его значение равно 1. (Пример 3); -
тождественно-ложным, если для любого набора значений аргументов его значение равно 0. (Пример 4); -
выполнимым, если существует хотя бы один набор значений аргументов, при котором его значение равно 1; -
опровержимым, если существует хотя бы один набор значений аргументов, при котором его значение равно 0.
Каждый рассматриваемый предикат является или тождественно-истинным, или тождественно-ложным, или выполнимым (опровержимым).
Множеством истинности предиката
Обозначают
Предикаты
Предикат
Пример. Найдите область истинности предикатов:
,
Решение:
2. Операции над предикатами.
На предикаты естественным образом переносятся все операции (логические связки), которые мы проделывали над высказываниями.
При образовании новых предикатов из данных с помощью операций логики высказываний считаем, что символ отрицания «сильнее» чем конъюнкция, конъюнкция – «сильнее» дизъюнкции, дизъюнкция – «сильнее» импликации, импликация – «сильнее» эквивалентности, т.е. остаются в силе те же соглашения, по которым можно опускать скобки в формулах.
-
Предикат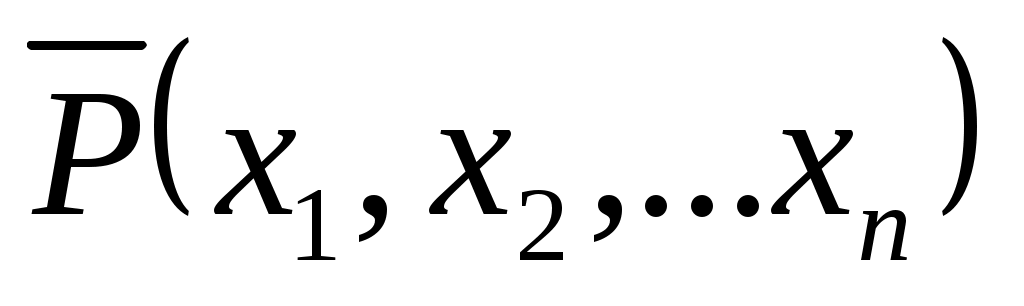 на множестве
на множестве 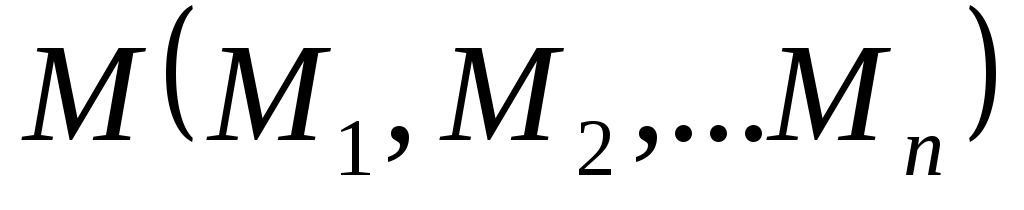 является тождественно-истинным тогда и только тогда, когда предикат
является тождественно-истинным тогда и только тогда, когда предикат на множестве
на множестве 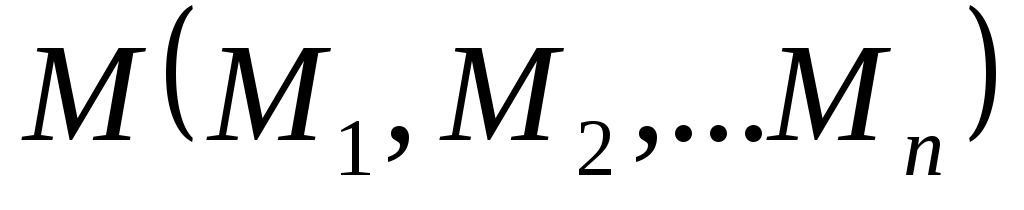 - ложный.
- ложный. -
Предикат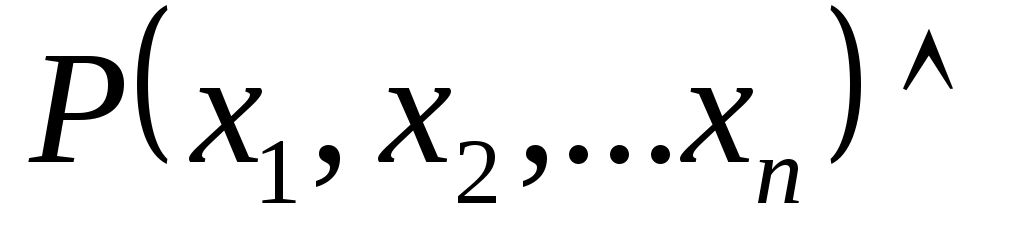
 на множестве
на множестве 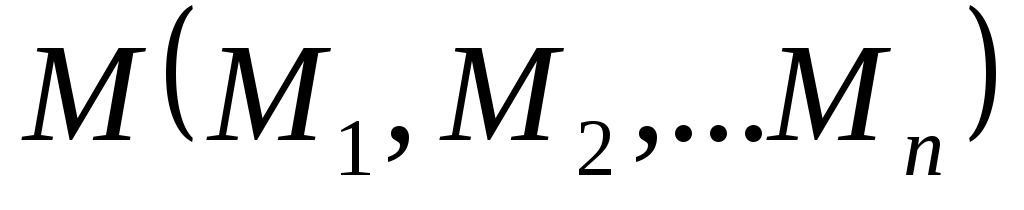 является тождественно-истинным тогда и только тогда, когда оба предиката
является тождественно-истинным тогда и только тогда, когда оба предиката  и
и  на множестве
на множестве 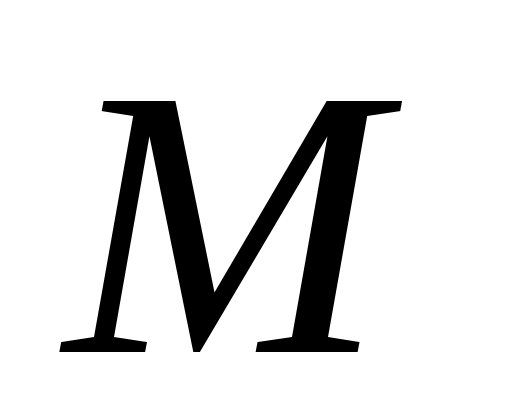 тождественно-истинные.
тождественно-истинные. -
Предикат

 на множестве
на множестве 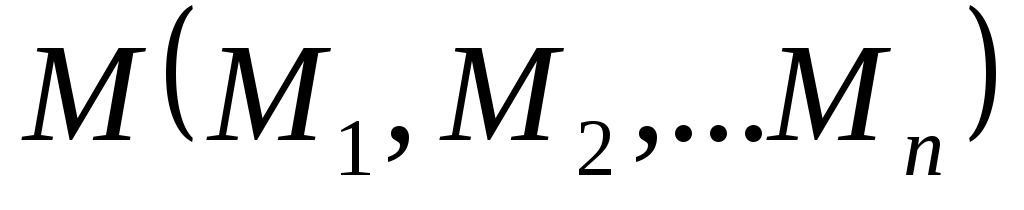 является тождественно-ложным тогда и только тогда, когда оба предиката
является тождественно-ложным тогда и только тогда, когда оба предиката  и
и  на множестве
на множестве 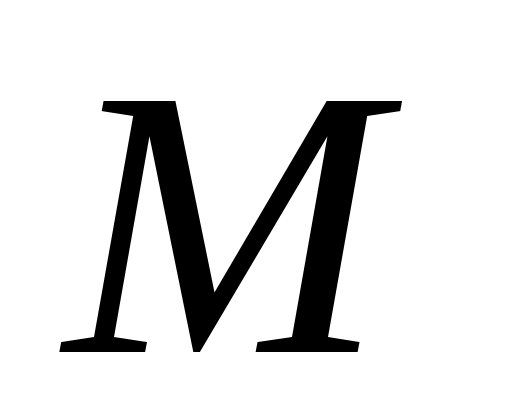 тождественно-ложные.
тождественно-ложные. -
Предикат

 на множестве
на множестве 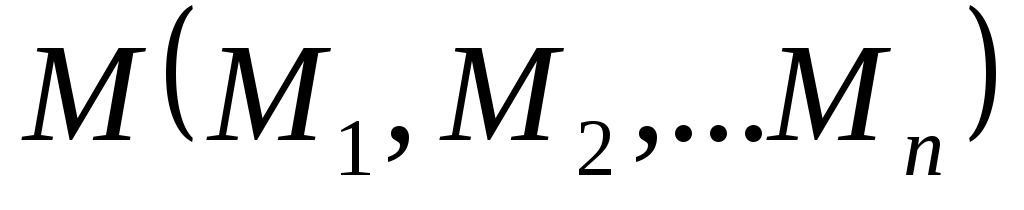 является тождественно-ложным тогда и только тогда, когда
является тождественно-ложным тогда и только тогда, когда  - тождественно-истинный, а
- тождественно-истинный, а  - тождественно-ложный на множестве
- тождественно-ложный на множестве 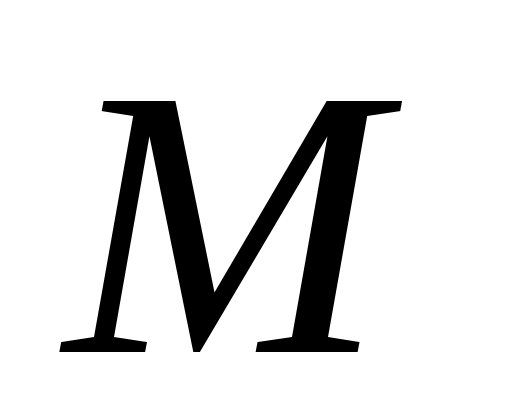 .
. -
Предикат

 на множестве
на множестве 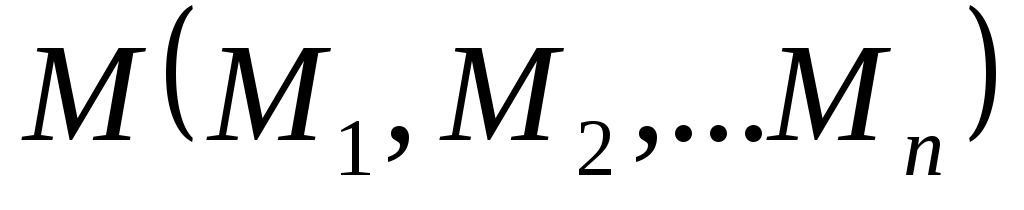 является тождественно-истинным тогда и только тогда, когда предикаты
является тождественно-истинным тогда и только тогда, когда предикаты  и
и  равносильны на множестве
равносильны на множестве 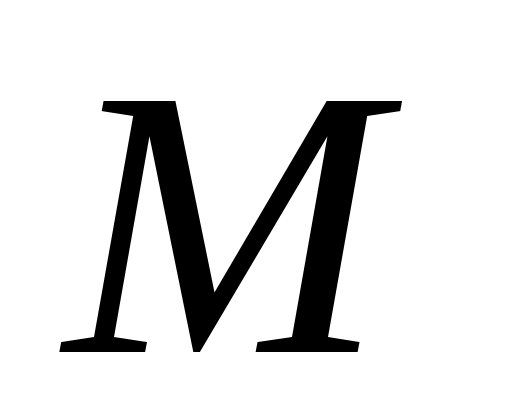 .
.