Файл: Методические указания по выполнению контрольной работы по учебной дисциплине ен. 02 Элементы математической логики.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 205
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- СДНФ
Алгоритм построения СКНФ с помощью равносильных преобразований:
1) приводим исходную формулу к КНФ;
2) если в элементарную дизъюнкцию некоторая переменная входит со своим отрицанием, то удаляем эту конъюнкцию из КНФ;
3) если в элементарную дизъюнкцию некоторая переменная входит несколько раз, то удаляем эти переменные кроме одной;
4) если в некоторую элементарную дизъюнкцию некоторая переменная или переменные не входят, то заменяем её на эквивалентную форму, добавляя к ней одну или несколько переменных в виде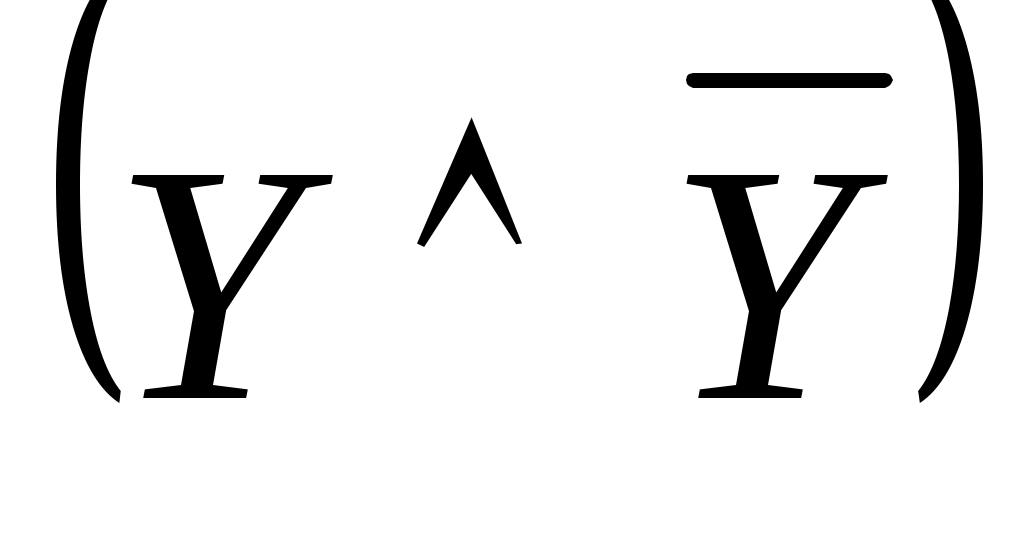 и, применяя закон дистрибутивности, приводим формулу к КНФ;
и, применяя закон дистрибутивности, приводим формулу к КНФ;
5) если в полученной КНФ имеется несколько одинаковых элементарных конъюнкций, то оставляем только одну из них.
В результате получаем СКНФ.
Пример:
Пусть дана КНФ функции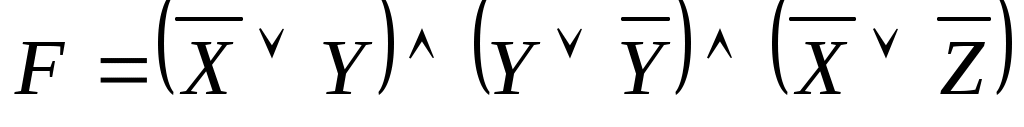 . Найти СКНФ функции.
. Найти СКНФ функции.
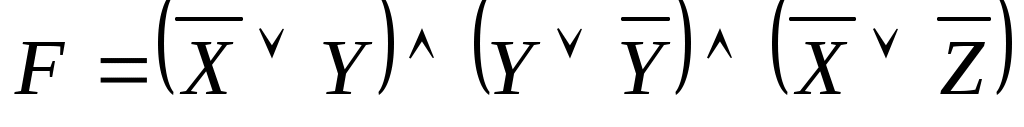

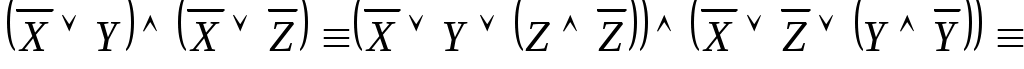
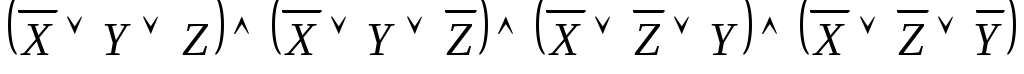

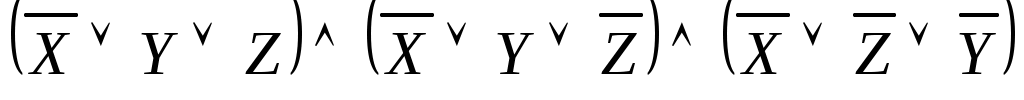
- СКНФ.
В алгебре высказываний существуют алгоритмы для формул, с помощью которых можно сказать, является ли формула тождественно истинной, тождественно ложной или выполнимой.
Рассмотрим следующие алгоритмы:
1) Для определения типа формулы надо построить ДНФ (КНФ) и
проверить критерий ложности (критерий истинности). Если критерий выполнен, то формула тождественно ложна (тождественно истинна), если нет, то строим КНФ (ДНФ) и проверяем критерий истинности
(критерий ложности), если критерий выполнен, то формула тождественно истинна (тождественно ложна) в противном случае, формула только выполнима.
2) Для определения типа формулы надо построить СДНФ или СКНФ. Если СДНФ построена, то формула не является тождественно ложной. Далее считаем число слагаемых в СДНФ: если их ,где n - число переменных, от которых зависит формула, то формула тождественно истинна, в противном случае выполнима.
,где n - число переменных, от которых зависит формула, то формула тождественно истинна, в противном случае выполнима.
Если СКНФ построена, то формула не тождественно истинна. Если число слагаемых в СКНФ равно , где n - число переменных, то формула тождественно ложна, в противном случае формула выполнима.
, где n - число переменных, то формула тождественно ложна, в противном случае формула выполнима.
БУЛЕВЫ ФУНКЦИИ.
1. Понятие булевой функции.
Булевы функции получили своё название по имени замечательного английского математика Джорджа Буля (1815-1864), который первым начал применять математические методы в логике.
Операции над высказываниями (отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности) можно рассматривать как определение некоторого действия над символами 0 и 1, т.е. как определение некоторой функции, заданной на двухэлементном множестве {0,1} и принимающей значения на том же множестве.
Символом 0 обозначалось любое ложное высказывание, а символом 1 – любое истинное.
Например, отрицание представляет собой в этом смысле
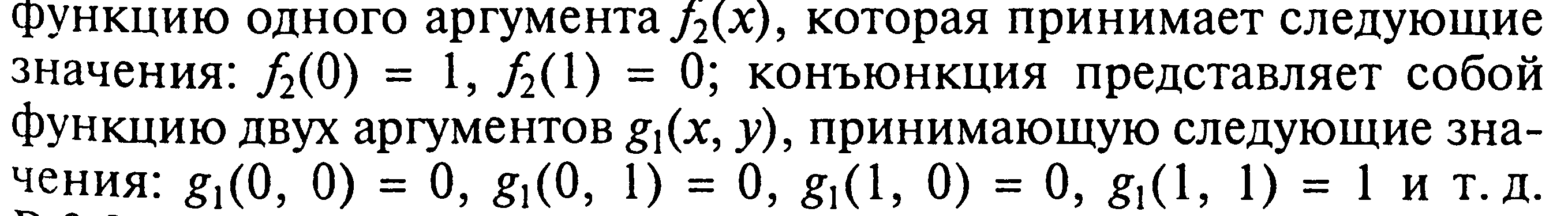

Кроме того, установим соответствие между знаками логических связок и булевых функций
Примечание: вместо знака конъюнкции при записи формул булевых функций может быть отсутствие знака между переменными.
Булева функция от одного аргумента
Булевой функцией от одного аргумента называется функция f
, заданная на множестве из двух элементов и принимающая значения на том же двухэлементном множестве.
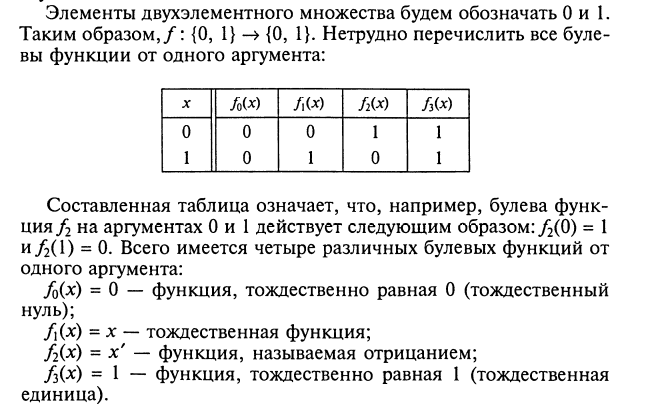
Булева функция от двух аргументов
Булевой функцией от двух аргументов называется функция g, заданная на множестве {0,1} {0,1} и принимающая значения на двухэлементном множестве{0,1}. Другими словами, булева функция от двух элементов сопоставляет любой упорядоченной паре, составленной из элементов 0 и 1 (а таких упорядоченных пар будет четыре), либо 0, либо 1.
{0,1} и принимающая значения на двухэлементном множестве{0,1}. Другими словами, булева функция от двух элементов сопоставляет любой упорядоченной паре, составленной из элементов 0 и 1 (а таких упорядоченных пар будет четыре), либо 0, либо 1.


Булева функция от n аргументов

2. Свойства булевых функций.
Две булевы функции называются равными , если для любых одинаковых наборов значений переменных обе функции принимают одинаковые значения.
Количество булевых функций от n переменных равно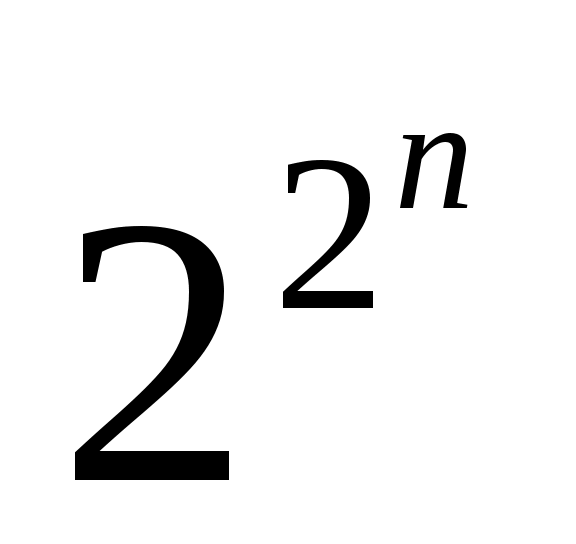
Таким образом, булевых функций от одной переменной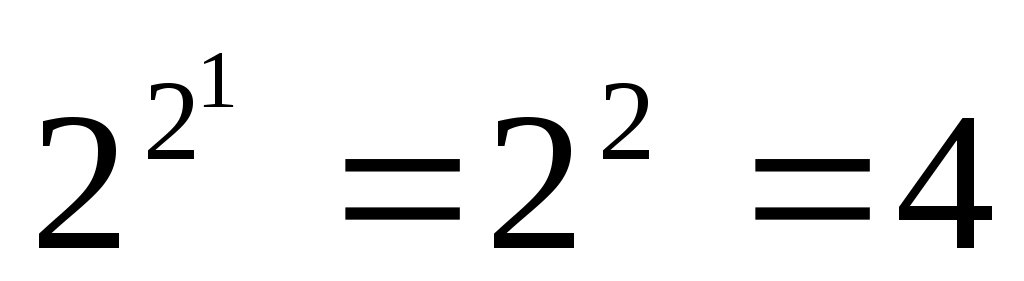 ,
,
от двух переменных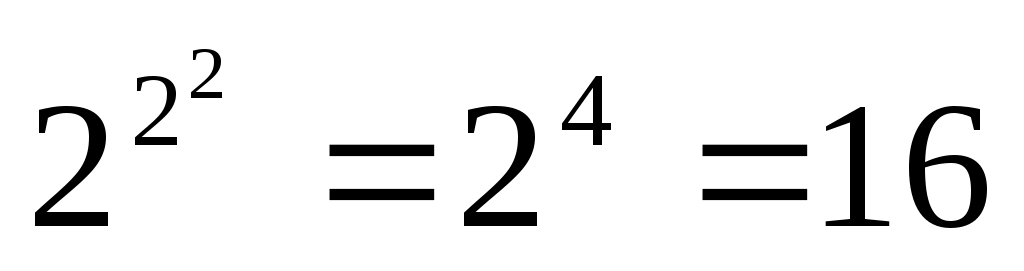 , и.т.д
, и.т.д
Операции булевой алгебры называются булевыми операциями, они подчиняются таким же законам, что и операции над высказываниями
Применение булевых операции не зависит от того каким путем получены значения переменных, т.е. первичны они или вторичны. Поэтому законы остаются справедливыми, если подставить вместо переменных любые формулы, которые являются логическими функциями. Последовательное выполняемые эквивалентные преобразования, позволяют доказывать эквивалентность формул более эффективно, чем их вычисление на наборах значений переменных. При этом используют следующие приёмы:
При упрощении формул используют следующие свойства:
Свойства конъюнкции, дизъюнкции и отрицания:
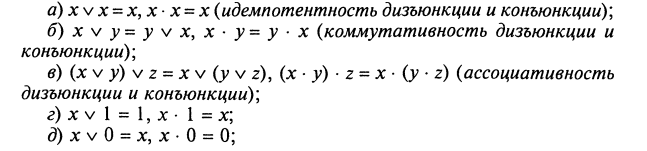
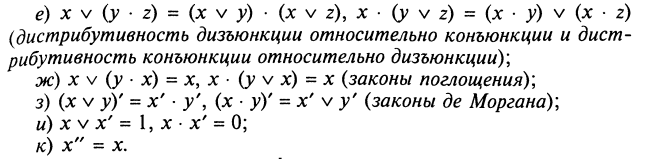
л)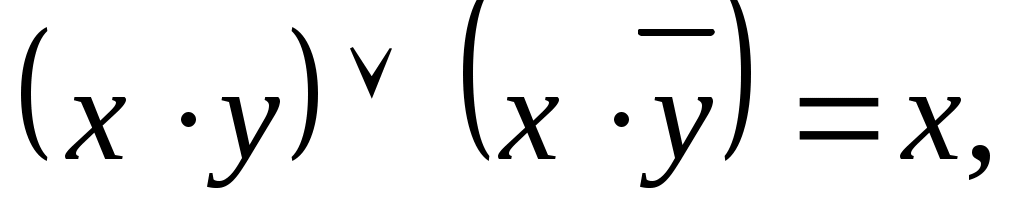
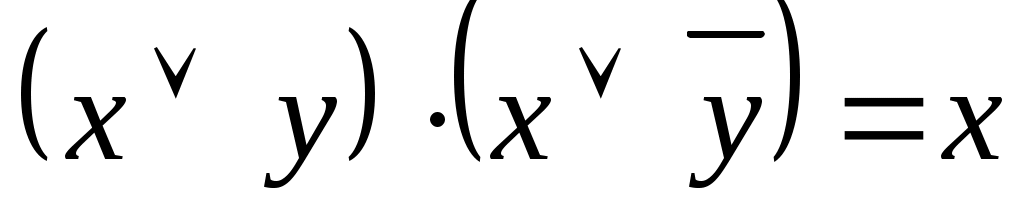 (законы склеивания)
(законы склеивания)
Свойства импликации, эквивалентности и отрицания:

Равенства, выражающие одни булевы функции через другие
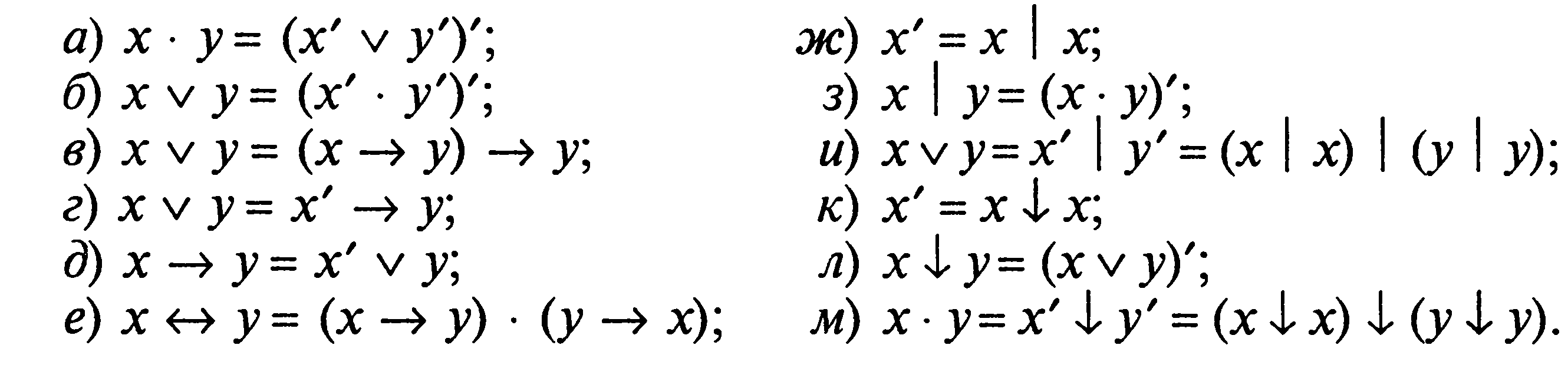
Примеры:
Решение: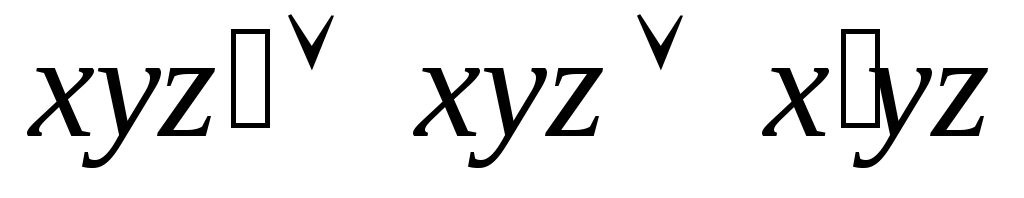

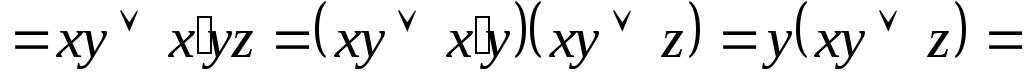
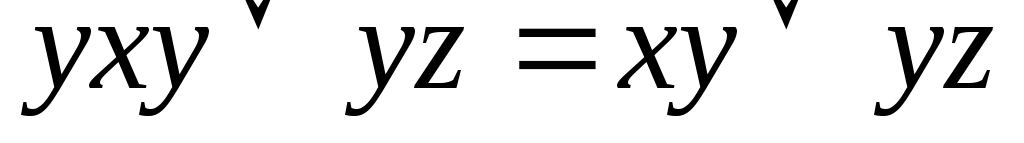
Решение: Составим таблицу истинности для левой и правой частей уравнения
Алгоритм построения СКНФ с помощью равносильных преобразований:
1) приводим исходную формулу к КНФ;
2) если в элементарную дизъюнкцию некоторая переменная входит со своим отрицанием, то удаляем эту конъюнкцию из КНФ;
3) если в элементарную дизъюнкцию некоторая переменная входит несколько раз, то удаляем эти переменные кроме одной;
4) если в некоторую элементарную дизъюнкцию некоторая переменная или переменные не входят, то заменяем её на эквивалентную форму, добавляя к ней одну или несколько переменных в виде
5) если в полученной КНФ имеется несколько одинаковых элементарных конъюнкций, то оставляем только одну из них.
В результате получаем СКНФ.
Пример:
Пусть дана КНФ функции
- СКНФ.
В алгебре высказываний существуют алгоритмы для формул, с помощью которых можно сказать, является ли формула тождественно истинной, тождественно ложной или выполнимой.
Рассмотрим следующие алгоритмы:
1) Для определения типа формулы надо построить ДНФ (КНФ) и
проверить критерий ложности (критерий истинности). Если критерий выполнен, то формула тождественно ложна (тождественно истинна), если нет, то строим КНФ (ДНФ) и проверяем критерий истинности
(критерий ложности), если критерий выполнен, то формула тождественно истинна (тождественно ложна) в противном случае, формула только выполнима.
2) Для определения типа формулы надо построить СДНФ или СКНФ. Если СДНФ построена, то формула не является тождественно ложной. Далее считаем число слагаемых в СДНФ: если их
Если СКНФ построена, то формула не тождественно истинна. Если число слагаемых в СКНФ равно
БУЛЕВЫ ФУНКЦИИ.
1. Понятие булевой функции.
Булевы функции получили своё название по имени замечательного английского математика Джорджа Буля (1815-1864), который первым начал применять математические методы в логике.
Операции над высказываниями (отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности) можно рассматривать как определение некоторого действия над символами 0 и 1, т.е. как определение некоторой функции, заданной на двухэлементном множестве {0,1} и принимающей значения на том же множестве.
Символом 0 обозначалось любое ложное высказывание, а символом 1 – любое истинное.
Например, отрицание представляет собой в этом смысле
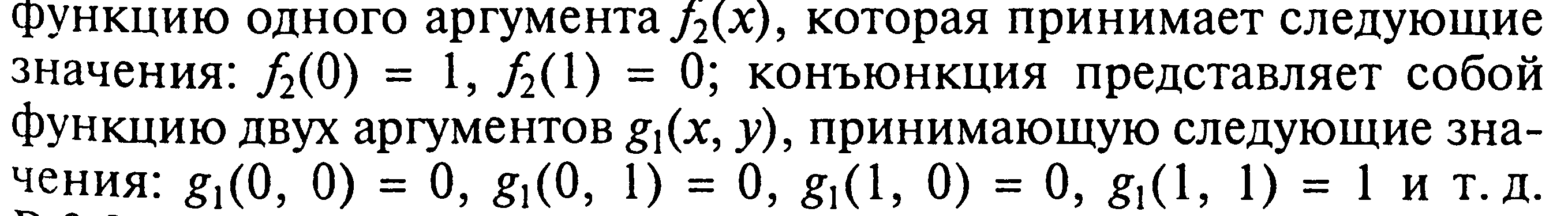

Кроме того, установим соответствие между знаками логических связок и булевых функций
-
Логические связки
ˉ




Булевы функции
ˊ
·



Примечание: вместо знака конъюнкции при записи формул булевых функций может быть отсутствие знака между переменными.
Булева функция от одного аргумента
Булевой функцией от одного аргумента называется функция f
, заданная на множестве из двух элементов и принимающая значения на том же двухэлементном множестве.

Булева функция от двух аргументов
Булевой функцией от двух аргументов называется функция g, заданная на множестве {0,1}


Булева функция от n аргументов

2. Свойства булевых функций.
Две булевы функции называются равными , если для любых одинаковых наборов значений переменных обе функции принимают одинаковые значения.
Количество булевых функций от n переменных равно
Таким образом, булевых функций от одной переменной
от двух переменных
Операции булевой алгебры называются булевыми операциями, они подчиняются таким же законам, что и операции над высказываниями
Применение булевых операции не зависит от того каким путем получены значения переменных, т.е. первичны они или вторичны. Поэтому законы остаются справедливыми, если подставить вместо переменных любые формулы, которые являются логическими функциями. Последовательное выполняемые эквивалентные преобразования, позволяют доказывать эквивалентность формул более эффективно, чем их вычисление на наборах значений переменных. При этом используют следующие приёмы:
-
упрощение формул, т.е. получение эквивалентных формул с меньшим числом символов; -
приведение формул к ДНФ и в том числе к СДНФ; -
приведение формул к КНФ и в том числе к СКНФ.
При упрощении формул используют следующие свойства:
Свойства конъюнкции, дизъюнкции и отрицания:
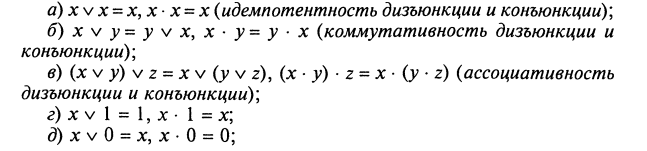
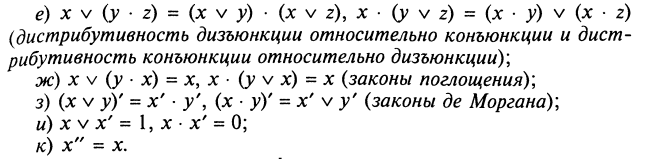
л)
Свойства импликации, эквивалентности и отрицания:

Равенства, выражающие одни булевы функции через другие
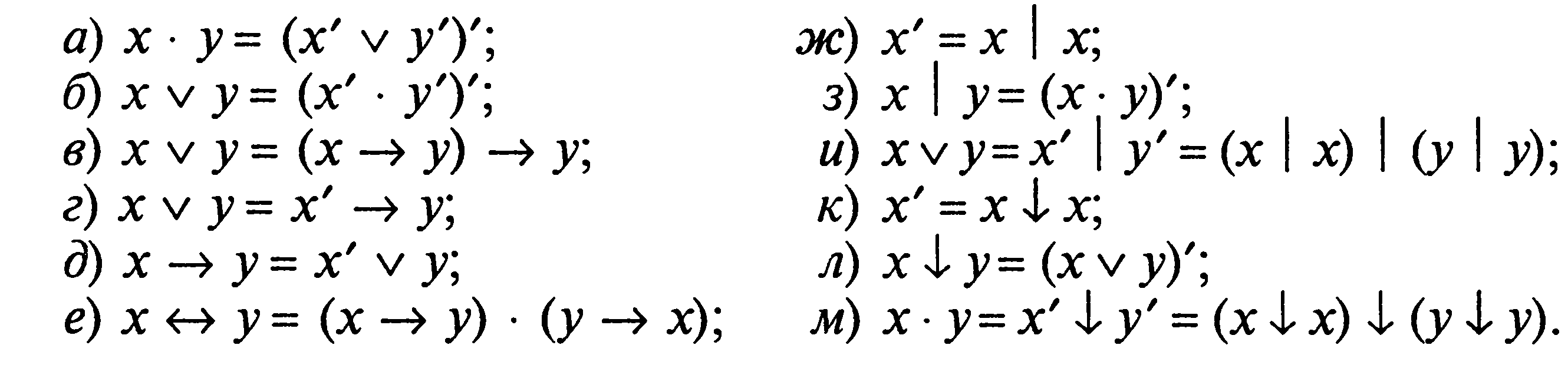
Примеры:
-
Упростите выражение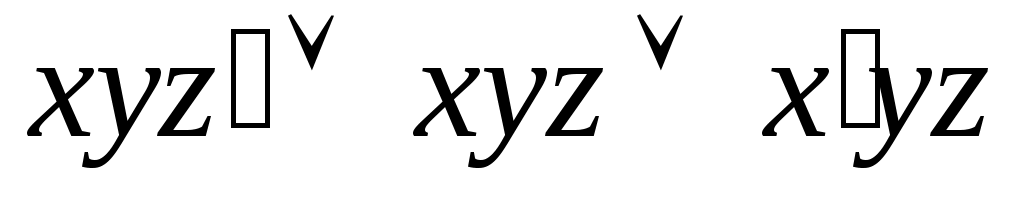 с помощью свойств булевых функций
с помощью свойств булевых функций
Решение:
-
Решите булево уравнение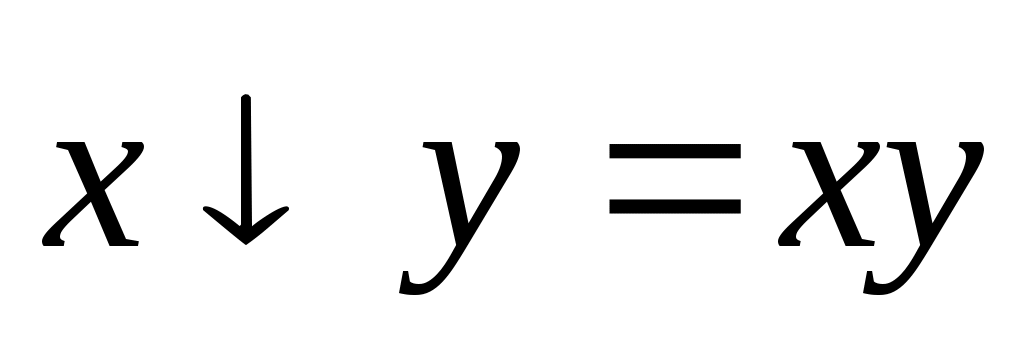
Решение: Составим таблицу истинности для левой и правой частей уравнения
| x | | | |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |