I. Организационный момент.

II. Устная работа.

1-й  б л о к. Актуализация знаний.

Назовите первые три члена последовательности:

а) a_n =  ;                 б) b_n = 3n – 1;                в) с_п = п² + 1.

Для последовательности, заданной первым членом и рекуррентной формулой, найдите второй и третий члены:

г) x₁ = 2, x_{п + 1} =  ;

д) у₁ = 3, у_{п + 1} = у_п² – 5.

2-й  б л о к. Актуализация знаний и создание проблемной ситуации.

Задать последовательность с помощью формулы п-го члена или рекуррентной формулы.

Последовательность	Формула
а) –2; 0; 2; 4; …	х1 = –2; хп + 1 = хп+ 2
б) –5; 5; –5; 5; …	хп= (–1)п · 5
в) 2; 2,5; 3; 3,5; 4; …	х1 = 2; хп + 1 = хп+ 0,5
г) 1; 4; 9; 16; …	хп= п2
д) 1;   …	х1 = 2; хп + 1 =
е) 0; 10; 20; 30; 40; …	х1 = 0; хп + 1 = хп+ 10
ж) а; а + 3; а + 6; а + 9; …	х1 = а; хп + 1 = хп+ 3

После заполнения таблицы анализируем полученные результаты и замечаем, что последовательности а), в), е) и ж) – одинакового вида, а именно: задаются рекуррентным способом и каждый член, начиная со второго, получается прибавлением к предыдущему числа (2; 0,5; 10; 3).

Учащиеся «открыли» определенный вид последовательности. Следует сказать, что такие последовательности называются «арифметическая прогрессия», и попросить учащихся попробовать самостоятельно сформулировать определение такой прогрессии на основе выделенных ими характеристических свойств.

---

III. Объяснение нового материала.

1. Определение. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

(а_п) – арифметическая прогрессия, если для любого п  N выполняется условие а_{п + 1} = а_п + d, где d – некоторое число. Число d называется «разностью арифметической прогрессии», так как из определения следует, что а_{п + 1} – а_п = d.

Далее следует привести примеры арифметических прогрессий, причем следует варьировать значение d (положительные числа; отрицательные; нуль; дробные).

П р и м е р ы  арифметических прогрессий:

1) а₁ = 1, d = 1.

1; 2; 3; 4; … (последовательные натуральные числа).

2) а₁ = 1, d = 2.

1; 3; 5; 6; … (последовательность положительных

                        нечетных чисел).

3) а₁ = –2, d = –2.

–2; –4; –6; –8; –10; … (последовательность отрицательных

четных чисел).

4) а₁ = 7, d = 0.

7; 7; 7; 7; … (постоянная последовательность).

5) а₁ = 1, d = 0,3.

1; 1,3; 1,6; 1,9; 2,2; …

Обращаем внимание, что если d > 0, то арифметическая прогрессия возрастающая, если d < 0 – убывающая, если d = 0 – постоянная.

2. Итак, учащиеся знают, что для того чтобы найти любой член арифметической  прогрессии  (или  задать  ее),  достаточно  знать  ее  первый член и разность. Следует подвести их к мысли, что это очень трудоемко, например:

(а_п) – арифметическая прогрессия, где а₁ = 2, d = 27. Найти сотый член.

Пользуясь определением, нам нужно сделать 100 шагов. Это громоздко. Хотелось бы знать формулу для нахождения любого члена арифметической прогрессии только по первому члену, разности и порядковому номеру искомого члена.

Для вывода формулы пользуемся определением арифметической прогрессии:

а₁

а₂ = а₁ + d

а₃ = а₂ + d = (а₁ + d) + d = а₁ + 2d

а₄ = а₃ + d = (а₁ + 2d) + d = а₁ + 3d

а₅ = а₄ + d = (а₁ + 3d) + d = а₁ + 4d

а₆ = …                      = 

---

а₁ + 5d

                 … …

– формула п-го члена    арифметической прогрессии.

П р и м е р  1. (с_п) – арифметическая прогрессия,

с₁ = 0,62, d = 0,24; с₅₀ –?

с₅₀ = с₁ + d (50 – 1) = 0,62 + 0,24 · 49 = 12,38.

Этот пример на «прямое» использование формулы п-го члена арифметической прогрессии.

П р и м е р  2. Выяснить, является ли число –122 членом арифметической прогрессии (х_п):

23; 17,2; 11,4; 5,6; …

При рассмотрении этого примера пояснить, что для решения надо доказать, что существует п  N, при котором будет верна формула п-го члена:

–122 = 23 + (п – 1) · (–5,8), где

–5,8 = 17,2 – 23 – разность арифметической прогрессии.

IV. Формирование умений и навыков.

Все задания, выполняемые учащимися на этом уроке, можно разбить на 3 типа:

1) На «узнавание» арифметической прогрессии, определение ее первого члена и разности.

2) На нахождение п-го члена арифметической прогрессии по определению и по формуле.

3) На запись формулы п-го члена по первому члену и разности, решение задач на «косвенное» использование формулы п-го члена (например, нахождение п).

Упражнения:

1. Решить устно:

а) Является ли последовательность арифметической прогрессией:

–3,5; –7; –10,5; –14; –17,5; …                         (Да.)

5; 5; 5; 5; …                                                    (Да.)

2; 12; 22; 23; 32; … ?                                               (Нет.)

б) Найти члены арифметической прогрессии, обозначенные буквами:

–10; –7; с₃; с₄; с₅; с₆

–3,4; –1,4; а₃; а₄

12; у₂; 20; у₄.

в) (а_п) – арифметическая прогрессия. Является ли арифметической прогрессией последовательность:

12а₁; 12а₂; …; 12а_п; …

3а₁ + 1; 3а₂ + 1; …; 12а_п + 1; … ?

2. № 575 (а, б), № 576 (а, в, д). Самостоятельное решение с последующей проверкой.

№ 577. Решение у доски с объяснением.

№ 579. Самостоятельное решение и одновременно на скрытых досках с проверкой.

3.

---

 № 584. Задание на «не прямое» применение формулы. Еще раз подчеркнуть, что с помощью этой формулы можно находить следующие величины: а_п; а₁; d; п.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Что называется арифметической прогрессией?

– Как задается арифметическая прогрессия?

– Назовите формулу п-го члена арифметической прогрессии.

Домашнее задание: № 575 (в, г); № 576 (б, г, е); № 586; № 599.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У р о к  60                                                                                           Дата:
СВОЙСТВО АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ

Цели: вывести и доказать характеристическое свойство арифметической прогрессии; формировать умения применять свойство арифметической прогрессии при решении задач; продолжить формирование навыков применения  определения  арифметической  прогрессии  и  формулы  п-го члена.

Ход урока

I. Организационный момент.

II. Математический диктант.

Работа выполняется по вариантам (в квадратных скобках задание, относящееся ко второму варианту).

1) У арифметической прогрессии первый член 4 [6], второй член 6 [2]. Найдите разность d.

2) У арифметической прогрессии первый член 6 [4], второй член 2 [6]. Найдите третий член.

3) Найдите десятый [восьмой] член арифметической прогрессии, если ее первый член равен 1, а разность 4 [5].

4) Является ли последовательность четных [нечетных] чисел арифметической прогрессией?

5) а_п – арифметическая прогрессия. Выразите через а₁ и d:

а₁₀; а_2k; a_{k + 3} [a₂₀; a_k; a_{2k + 1}].

О т в е т ы:           1) 2 [–4];

                              2) –2 [8];

                              3) 37 [36];

                              4) Да [Да];

                              5) а₁₀ = а₁ + 9d                      [а₂₀ = а₁ + 19d];

                                  а_2k = а₁ + d (2k – 1)           [а_k = а₁ + d

---

 (k – 1)];

                                  a_{k + 3} = а₁ + d (k + 2)          [a_{2k + 1} = а₁ + 2dk].

III. Объяснение нового материала.

У с т н о е   з а д а н и е:

Дана арифметическая прогрессия (х_п): 2; 5; 8; 11; 14.

Вычислить:           =                             (5.)

                                =                             (8.)

                                =                             (11.)

Замечаем интересное свойство и формируем его – «Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов».

Так как мы это предположили исходя из рассмотрения конкретной последовательности, данное утверждение следует доказать:

 Пусть (х_п) – арифметическая прогрессия, тогда

х_п – х_{п – 1} = х_{п + 1} – х_п, то есть

2х_п = х_{п – 1} + х_{п + 1},

хп =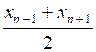

Следует обратить особое внимание учащихся, что это утверждение – свойство арифметической прогрессии. А если мы сформулируем обратное утверждение и сможем его доказать, то как будет оно называться? Это будет признак арифметической прогрессии: «Если в последовательности (х_п) каждый член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией».

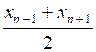 Пусть х_п =  , где п ≥ 2, тогда 2х_п = х_п

---

Смотрите также файлы

• Отчёт по слесарной практике.docx

• В таблице представлены данные о полезности товара А. Определите среднюю и предельную полезность единицы товара А.docx

• Мишель де монтень Насретдинова П. Д., 329 группа.pptx

• 1. Контакт глазами.docx

• Реферат по дисциплине на тему Экология и здоровье человека.docx