Ответ на первый вопрос ученики знают, как получить, такие задачи решались  ими  на  прошлых  занятиях.  Количество  изготовленных  изделий в первую, вторую и т. д. недели можно обозначить а₁, а₂,… а_п, …, причем (а_п) – арифметическая прогрессия с разностью d = 5 и первым членом а₁ = 15. За восьмую неделю ученик изготовил гончарных изделий:

а₈ = 15 + 5 (8 – 1) = 50.

Для ответа на второй вопрос ученики могут предложить только такой способ  решения:  подсчитать  количество  изделий,  выполненных за 2-ю, 3-ю, …, 10-ю неделю, и сложить. Это очень долго. А если в задаче нужно будет найти сумму ста членов арифметической прогрессии, тысячи? Возникает проблема – нужна общая формула.

2. Пример из истории математики.

С формулой суммы п первых членов арифметической прогрессии связан эпизод из жизни немецкого математика Карла Гаусса (1777–1855). Маленькому Карлу было 9 лет, когда учитель, занятый проверкой работ учеников, предложил классу сложить все натуральные числа от 1 до 100, рассчитывая надолго занять детей. Каково же было удивление преподавателя, когда через несколько минут Гаусс подошел к нему с верным ответом! Он подошел к решению творчески, заметив, что можно складывать числа не подряд, а парами: 1 + 100, 2 + 99, 3 + 98 … и т. д. Легко увидеть, что сумма чисел в каждой паре равна 101, а таких пар 50, значит общая сумма равна 101 · 50 = 5050.

А можно ли с помощью рассуждений, аналогичных тем, что проводил маленький Гаусс, найти сумму первых п членов любой арифметической прогрессии?

3. Вывод формулы.

Пусть (а_п) – арифметическая прогрессия.

Обозначим S_n сумму п первых членов арифметической прогрессии.

S_n = а₁ + а₂ + а₃ + а₄ + … + а_{п – 1} + а_п                       (1)

S_n = а_п + а_{п – 1} + а_{п – 2} + а_{п – 3} + … + а₂ + а₁                           (2)

Докажем, что сумма каждой пары членов прогрессии, расположенных друг под другом, равна а₁ + а_п.

a₂ + a_{n – 1} = (a₁ + d) + (a_n – d

---

) = a₁ + a_n;

a₃ + a_{n – 2} = (a₂ + d) + (a_{n – 1} – d) = a₂ + a_{n – 1} = a₁ + a_n;

a₄ + a_{n – 3} = (a₃ + d) + (a_{n – 2} – d) = a₃ + a_{n – 2} = a₁ + a_n   и т. д.

Число таких пар равно п. Складываем почленно (1) и (2) и получаем

2S_n = (a₁ + a_n) · n.

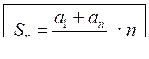– формула суммы п первых членов    арифметической прогрессии.

Обычно арифметическая прогрессия задается первым членом и разностью, поэтому удобно иметь еще формулу суммы п первых членов, выраженную через а₁ и d арифметической прогрессии.

S_n =   · n, а_п= а₁ + d (п – 1);

S_n =   · n;

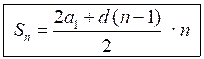– формула суммы п первых членов    арифметической прогрессии.

4. Пример.

Вернемся к задаче про ученика мастера. В течение 10 недель ученик мастера изготовил

S₁₀ =   · 10 = 375 изделий.

IV. Формирование умений и навыков.

Так как формул суммы п первых членов арифметической прогрессии две, то необходимо сперва выяснить, в заданиях какого вида лучше использовать каждую из них, а затем при решении упражнений анализировать условие и выбирать формулу.

Упражнения:

1) Найти сумму первых тридцати членов арифметической прогрессии 4; 5,5; …

Р е ш е н и е

а₁ = 4, d = 1,5, значит, по формуле II:

а₃₀

---

 =   · 30 = 772,5.

2) Найти сумму первых сорока членов последовательности (а_п), заданной формулой а_п = 5 · п – 4.

Последовательность  (а_п)  задана  формулой  вида  а_п = kn + b, где k = 5 и b = –4, значит, (а_п) – арифметическая прогрессия. Если применять формулу II, то для этого сперва надо найти а₁, а₂ , затем d как разность а₁ – а₂. Это неудобно, проще сразу найти а₁, а₄₀ и подставить в формулу I.

а₁ = 5 · 1 – 4 = 1; а₄ = 5 · 40 – 4 = 196;

S₄₀ =   = 3940.

3) № 603, № 604. На «прямое» применение формул I и II. Самостоятельное решение с последующей проверкой.

№ 606.

№ 608 (а). У доски с объяснением. Здесь необходимо «увидеть», что последовательность  слагаемых – арифметическая  прогрессия, где а₁ = 2, d = 2 и количество слагаемых равно п, можно применить формулу II. А можно задать эту прогрессию формулой а_п = 2п и применить формулу I.

---

V. Итоги урока.

– Назовите формулу суммы первых п членов арифметической прогрессии (2 вида).

– В каких случаях удобнее применять формулу I, II?

Домашнее задание: № 605, № 607, № 608 (б), № 621 (а).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У р о к  63                                                                    Дата:
ПРИМЕНЕНИЕ ФОРМУЛЫ СУММЫ ПЕРВЫХ п ЧЛЕНОВ
АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ

Цели: закреплять умения и навыки применения формулы суммы первых п членов арифметической прогрессии при решении задач; провести подготовку к контрольной работе.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Является ли арифметической прогрессией последовательность, заданная формулой:

а) х_п = 2п + 1;

б) у_п = п² – п;

в) z_n = –64?

2. Найдите разность арифметической прогрессии:

г) 17; 13; 9; …

д) (х_п), если х₁₀ = 4, х₁₂ = 14;

е) (у_п), если у_п = 3п – 0,5.

3. (а_п) – арифметическая прогрессия, вычислите:

ж) а₇, если а₁ = 1, d = –2;

з) а₁₀, если а_п = 17 · п – 100;

и) а₁₂, если а₁ = 0, а₂ = 3.

III. Проверочная работа.

Работа проводится по вариантом, задания на «прямое» применение формулы суммы п первых членов арифметической прогрессии.

В а р и а н т  1

1) Найдите сумму первых двенадцати членов арифметической прогрессии, если а₁ = 16,5; d = –1,5.

2) Найдите сумму первых сорока членов последовательности, заданной формулой а_п = 3п + 2.

3) Найдите  сумму  десяти  первых  членов  арифметической  прогрессии (а

---

_п), если а₁ = 8, а₇ = 26.

В а р и а н т  2

1) Найдите сумму первых десяти членов арифметической прогрессии, если а₁ = 18,5; d = –2,5.

2) Найдите сумму первых двадцати членов последовательности, заданной формулой х_п = 4п + 5.

3) Найдите сумму двенадцати первых членов арифметической прогрессии (а_п), если а₁ = 6, а₁₁ = 46.

О т в е т ы:

Задание	I вариант	II вариант
1	99	72,5
2	2540	940
3	215	336

IV. Формирование умений и навыков.

Все упражнения, решаемые на этом уроке, можно условно разделить на следующие виды:

1) На вычисление суммы первых п членов арифметической прогрессии по двум формулам (требует выбора формулы в зависимости от условия задачи).

2) На вычисление отдельных членов, числа членов, разности арифметической прогрессии по формулам суммы первых п членов.

3) На нахождение вышеперечисленных величин при наличии дополнительных условий и ограничений, сводящиеся к решению систем уравнений, неравенств.

Задания первого вида были выполнены в ходе проверочной работы.

Упражнения:

№ 609 (в), № 610, № 612, № 614, № 616. Решение у доски с комментариями.

Р е ш е н и е

№ 609 (в).

(а_п) – арифметическая прогрессия;

а_п = 4п, а_п ≤ 300;

4п ≤ 300;

п ≤ 75, значит, п = 75 – количество таких чисел.

а₁ = 4; а₇₅ = 4 · 75 = 300;

S₇₅ =   · 75 = 11400.

О т в е т: 11400.

№ 610.

В  этом  упражнении  задана  арифметическая  прогрессия  (а_п),  где
а₁ = 10; d = 3. Наши формулы позволяют находить сумму с первого по п-й член включительно, а требуется найти с 15-го по 30-й включительно. Заметим, что  мы  можем  найти  суммы членов арифметической прогрессии с 1-го по 30-й и с 1-го по 14-й включительно, их разность и даст искомый результат.

---

Смотрите также файлы

• Отчёт по слесарной практике.docx

• В таблице представлены данные о полезности товара А. Определите среднюю и предельную полезность единицы товара А.docx

• Мишель де монтень Насретдинова П. Д., 329 группа.pptx

• 1. Контакт глазами.docx

• Реферат по дисциплине на тему Экология и здоровье человека.docx