ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1039
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– 1 + хп + 1,
хп – хп – 1 = хп + 1 – хп, то есть разность между последующим и предыдущим членами последовательности (хп) остается постоянной. Значит, (хп) – арифметическая прогрессия
.
IV. Формирование умений и навыков.
Задачи, решаемые на этом уроке, более разнообразны по сравнению с предыдущим уроком. Теперь мы можем использовать определение арифметической прогрессии, ее свойство и признак, формулу п-го члена.
Кроме того, появляются задачи, в тексте которых не задана арифметическая прогрессия в явном виде. Нужно «перевести» условие на математический язык, «увидеть» арифметическую прогрессию, решить задачу и формулировку ответа опять «перевести» на язык условия.
Упражнения:
1. № 580, № 585. Самостоятельное решение заданий на «прямое» применение формулы п-го члена и нахождения разности.
№ 582. Решение у доски с объяснениями. Необходимо самостоятельно задать арифметическую прогрессию (хп), где
х1 = 50 (м/мин) – скорость поезда в конце первой минуты;
d = 50 (м/мин) – увеличение скорости;
х20 –?
х20 = х1 + d (20 – 1);
х20 = 50 + 50 · 19 = 50 · 20 = 1000 (м/мин).
Обращаем внимание, что скорость принято выражать в км/ч, значит, ответ · 60 = 60 (км/ч).
№ 587.
2. № 589, № 593. Эти упражнения на неоднократное применение формулы п-го члена арифметической прогрессии, сводящиеся к решению системы уравнений либо неравенства.
Особое внимание следует уделить анализу условия. Решение полученной системы уравнений и неравенства ученики могут осуществить самостоятельно.
3. Упражнение на применение свойства арифметической прогрессии носит развивающий характер.
Первый член арифметической прогрессии равен 7. Найдите второй и третий ее члены, если известно, что они являются квадратами двух последовательных натуральных чисел.
Р е ш е н и е
Пусть (ап) – арифметическая прогрессия, где
а1 = 7;
а2 = п2;
а3 = (п + 1)2, п N.
По свойству арифметической прогрессии:
а2 = ;
а1 + а3 = 2а2;
7 + (п + 1)2 = 2п2;
п2 – 2п – 8 = 0;
п = 4 или п = –2. Так как п N, то –2 – не удовлетворяет условию.
а2 = 42 = 16;
а3
= 52 = 25.
V. Итоги урока.
– Сформулируйте свойство арифметической прогрессии.
– Сформулируйте признак арифметической прогрессии.
Домашнее задание: № 581, № 588, № 591; 594
У р о к 61 Дата:
ФОРМУЛА п-го ЧЛЕНА АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
(аналитическая)
Цели: вывести аналитическую формулу п-го члена арифметической прогрессии; формировать умения задавать арифметическую прогрессию аналитической и рекуррентной формулами; закрепить умения и навыки применения формул п-го члена и свойства арифметической прогрессии.
Ход урока
I. Организационный момент.
II. Проверка домашней работы.
1. № 594. У доски – решение с комментариями ученика.
Р е ш е н и е
d = –18,7 – (–20,3) = 1,6;
ап = –20,3 + 1,6 (п – 1);
ап = –21,9 + 1,6п.
Пусть ап > 0, тогда –21,9 + 1,6п > 0;
п > ;
п > 13,6875.
Значит, п = 14 – порядковый номер первого положительного члена арифметической прогрессии.
а14 = –21,9 + 1,6 · 14 = 0,5.
2. Ответы учащихся на вопросы по домашней работе.
III. Объяснение нового материала.
1. ап = а1 + d (п – 1) – формула п-го члена арифметической прогрессии. Запишем ее в виде ап = d · п + (а1 – d), так как (а1 – d) – некоторое число, то обозначим его b = а1 – d и k = d, тогда получаем, что любая арифметическая прогрессия может быть задана формулой вида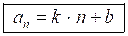
, где k и b – некоторые числа. Такие формулы мы встречали при изучении последовательностей. Делаем вывод, что арифметическую прогрессию можно задать не только рекуррентной
, но и аналитической формулой.
Более того, верно и обратное утверждение: последовательность (ап), заданная формулой вида ап= k · п + b, где k и b – некоторые числа, является арифметической прогрессией.
Найдем разность (п + 1)-го и п-го членов последовательности (ап):
ап + 1– ап = k (п + 1) + b – (kп + b) = kп + k + b – kп – b = k. Значит, при любом п справедливо ап + 1 = ап+ k и по определению (ап) – арифметическая прогрессия с разностью k.
IV. Формирование умений и навыков.
Упражнения:
№ 597. Можно решать устно.
№ 583. При решении этой задачи необходимо использовать сведения из курса геометрии (подобие треугольников). Обозначив А1В1 = х, получим А2В2 = 2х; А3В3 = 3х; … АпВп = п · х, где х = 1,5 (см), получим последовательность, заданную формулой АпВп = 1,5 · п, то есть формула имеет вид ап= kп + b, где k = 1,5; b = 0. Дальнейшие вычисления проводим, используя формулу п-го члена арифметической прогрессии.
V. Самостоятельная работа.
В а р и а н т 1
1. Зная первые два члена арифметической прогрессии 3,4; –0,2; …, найдите следующие за ними четыре ее члена.
2. В арифметической прогрессии (bп) известны b1 = –0,8, d = 4. Найдите b3; b24.
3. В арифметической прогрессии (хп) известны х1 = 14 и d = 0,5. Найдите номер члена прогрессии, равного 34.
4.* Мастерская изготовила в январе 106 изделий, а в каждый следующий месяц изготовляла на 12 изделий больше, чем в предыдущий. Сколько изделий изготовила мастерская в июне?
В а р и а н т 2
1. Зная первые два члена арифметической прогрессии 2,8; –0,4; …, найдите следующие за ними четыре ее члена.
2. В арифметической прогрессии (ап) известны а1 = –1,2, d = 3. Найдите а4; а21.
3. В арифметической прогрессии (
bп) известны b1 = 12 и d = 3. Найдите номер члена прогрессии, равного 27.
4.* Бригада стеклодувов изготовила в январе 80 изделий, а в каждый следующий месяц изготовляла на 17 изделий больше, чем в предыдущий. Сколько изделий изготовила мастерская в августе?
Упражнения под звездочкой не обязательны для выполнения.
О т в е т ы:
Так как самостоятельная работа носит обучающий характер, то целесообразно проверить ее на этом уроке.
VI. Итоги урока.
Анализ результатов самостоятельной работы.
Домашнее задание: № 590, № 592, № 594; № 598.
У р о к 62 Дата:
НАХОЖДЕНИЕ СУММЫ ПЕРВЫХ пЧЛЕНОВ
АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
Цели: вывести формулу суммы первых п членов арифметической прогрессии; формировать умение применять эту формулу при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
У с т н о:
1. Сформулируйте определение арифметической прогрессии.
2. Приведите пример арифметической прогрессии.
3. Сформулируйте определение разности арифметической прогрессии.
4. Назовите формулу п-го члена арифметической прогрессии.
П и с ь м е н н о:
III. Объяснение нового материала.
1. Создание проблемной ситуации.
З а д а ч а. Ученик мастера изготовил в первую неделю работы 15 гончарных изделий, а в каждую следующую неделю изготовлял на 5 изделий больше, чем в предыдущую. Сколько изделий ученик изготовил за восьмую неделю? Сколько изделий ученик изготовил всего в течение десяти недель?
хп – хп – 1 = хп + 1 – хп, то есть разность между последующим и предыдущим членами последовательности (хп) остается постоянной. Значит, (хп) – арифметическая прогрессия
.IV. Формирование умений и навыков.
Задачи, решаемые на этом уроке, более разнообразны по сравнению с предыдущим уроком. Теперь мы можем использовать определение арифметической прогрессии, ее свойство и признак, формулу п-го члена.
Кроме того, появляются задачи, в тексте которых не задана арифметическая прогрессия в явном виде. Нужно «перевести» условие на математический язык, «увидеть» арифметическую прогрессию, решить задачу и формулировку ответа опять «перевести» на язык условия.
Упражнения:
1. № 580, № 585. Самостоятельное решение заданий на «прямое» применение формулы п-го члена и нахождения разности.
№ 582. Решение у доски с объяснениями. Необходимо самостоятельно задать арифметическую прогрессию (хп), где
х1 = 50 (м/мин) – скорость поезда в конце первой минуты;
d = 50 (м/мин) – увеличение скорости;
х20 –?
х20 = х1 + d (20 – 1);
х20 = 50 + 50 · 19 = 50 · 20 = 1000 (м/мин).
Обращаем внимание, что скорость принято выражать в км/ч, значит, ответ · 60 = 60 (км/ч).
№ 587.
2. № 589, № 593. Эти упражнения на неоднократное применение формулы п-го члена арифметической прогрессии, сводящиеся к решению системы уравнений либо неравенства.
Особое внимание следует уделить анализу условия. Решение полученной системы уравнений и неравенства ученики могут осуществить самостоятельно.
3. Упражнение на применение свойства арифметической прогрессии носит развивающий характер.
Первый член арифметической прогрессии равен 7. Найдите второй и третий ее члены, если известно, что они являются квадратами двух последовательных натуральных чисел.
Р е ш е н и е
Пусть (ап) – арифметическая прогрессия, где
а1 = 7;
а2 = п2;
а3 = (п + 1)2, п N.
По свойству арифметической прогрессии:
а2 = ;
а1 + а3 = 2а2;
7 + (п + 1)2 = 2п2;
п2 – 2п – 8 = 0;
п = 4 или п = –2. Так как п N, то –2 – не удовлетворяет условию.
а2 = 42 = 16;
а3
= 52 = 25.
V. Итоги урока.
– Сформулируйте свойство арифметической прогрессии.
– Сформулируйте признак арифметической прогрессии.
Домашнее задание: № 581, № 588, № 591; 594
У р о к 61 Дата:
ФОРМУЛА п-го ЧЛЕНА АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
(аналитическая)
Цели: вывести аналитическую формулу п-го члена арифметической прогрессии; формировать умения задавать арифметическую прогрессию аналитической и рекуррентной формулами; закрепить умения и навыки применения формул п-го члена и свойства арифметической прогрессии.
Ход урока
I. Организационный момент.
II. Проверка домашней работы.
1. № 594. У доски – решение с комментариями ученика.
Р е ш е н и е
d = –18,7 – (–20,3) = 1,6;
ап = –20,3 + 1,6 (п – 1);
ап = –21,9 + 1,6п.
Пусть ап > 0, тогда –21,9 + 1,6п > 0;
п > ;
п > 13,6875.
Значит, п = 14 – порядковый номер первого положительного члена арифметической прогрессии.
а14 = –21,9 + 1,6 · 14 = 0,5.
2. Ответы учащихся на вопросы по домашней работе.
III. Объяснение нового материала.
1. ап = а1 + d (п – 1) – формула п-го члена арифметической прогрессии. Запишем ее в виде ап = d · п + (а1 – d), так как (а1 – d) – некоторое число, то обозначим его b = а1 – d и k = d, тогда получаем, что любая арифметическая прогрессия может быть задана формулой вида
, где k и b – некоторые числа. Такие формулы мы встречали при изучении последовательностей. Делаем вывод, что арифметическую прогрессию можно задать не только рекуррентной
, но и аналитической формулой.
Более того, верно и обратное утверждение: последовательность (ап), заданная формулой вида ап= k · п + b, где k и b – некоторые числа, является арифметической прогрессией.
Найдем разность (п + 1)-го и п-го членов последовательности (ап):ап + 1– ап = k (п + 1) + b – (kп + b) = kп + k + b – kп – b = k. Значит, при любом п справедливо ап + 1 = ап+ k и по определению (ап) – арифметическая прогрессия с разностью k.
IV. Формирование умений и навыков.
Упражнения:
№ 597. Можно решать устно.
№ 583. При решении этой задачи необходимо использовать сведения из курса геометрии (подобие треугольников). Обозначив А1В1 = х, получим А2В2 = 2х; А3В3 = 3х; … АпВп = п · х, где х = 1,5 (см), получим последовательность, заданную формулой АпВп = 1,5 · п, то есть формула имеет вид ап= kп + b, где k = 1,5; b = 0. Дальнейшие вычисления проводим, используя формулу п-го члена арифметической прогрессии.
V. Самостоятельная работа.
В а р и а н т 1
1. Зная первые два члена арифметической прогрессии 3,4; –0,2; …, найдите следующие за ними четыре ее члена.
2. В арифметической прогрессии (bп) известны b1 = –0,8, d = 4. Найдите b3; b24.
3. В арифметической прогрессии (хп) известны х1 = 14 и d = 0,5. Найдите номер члена прогрессии, равного 34.
4.* Мастерская изготовила в январе 106 изделий, а в каждый следующий месяц изготовляла на 12 изделий больше, чем в предыдущий. Сколько изделий изготовила мастерская в июне?
В а р и а н т 2
1. Зная первые два члена арифметической прогрессии 2,8; –0,4; …, найдите следующие за ними четыре ее члена.
2. В арифметической прогрессии (ап) известны а1 = –1,2, d = 3. Найдите а4; а21.
3. В арифметической прогрессии (
bп) известны b1 = 12 и d = 3. Найдите номер члена прогрессии, равного 27.
4.* Бригада стеклодувов изготовила в январе 80 изделий, а в каждый следующий месяц изготовляла на 17 изделий больше, чем в предыдущий. Сколько изделий изготовила мастерская в августе?
Упражнения под звездочкой не обязательны для выполнения.
О т в е т ы:
| Задание | I вариант | II вариант |
| 1 | –3,8; –7,4; –11; –14,6 | –3,6; –6,8; –10; –13,2 |
| 2 | b3 = 7,2; b24 = 71,2 | а4 = 7,8; а21 = 58,8 |
| 3 | п = 41 | п = 6 |
| 4 | 166 | 199 |
Так как самостоятельная работа носит обучающий характер, то целесообразно проверить ее на этом уроке.
VI. Итоги урока.
Анализ результатов самостоятельной работы.
Домашнее задание: № 590, № 592, № 594; № 598.
У р о к 62 Дата:
НАХОЖДЕНИЕ СУММЫ ПЕРВЫХ пЧЛЕНОВ
АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ
Цели: вывести формулу суммы первых п членов арифметической прогрессии; формировать умение применять эту формулу при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
У с т н о:
1. Сформулируйте определение арифметической прогрессии.
2. Приведите пример арифметической прогрессии.
3. Сформулируйте определение разности арифметической прогрессии.
4. Назовите формулу п-го члена арифметической прогрессии.
П и с ь м е н н о:
| В а р и а н т 1. № 578 (а). | В а р и а н т 2. № 578 (б). |
III. Объяснение нового материала.
1. Создание проблемной ситуации.
З а д а ч а. Ученик мастера изготовил в первую неделю работы 15 гончарных изделий, а в каждую следующую неделю изготовлял на 5 изделий больше, чем в предыдущую. Сколько изделий ученик изготовил за восьмую неделю? Сколько изделий ученик изготовил всего в течение десяти недель?