ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1029
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Найдите стороны прямоугольника.
3. Не выполняя построения, найдите координаты точек пересечения параболы у = х2 – 8 и прямой х + у = 4.
4. Решите систему уравнений:
5. Изобразите на координатной плоскости множество решений системы неравенств:
В а р и а н т 4
1. Решите систему уравнений:
2. Одна из сторон прямоугольника на 4 м больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 45 м2.
3. Не выполняя построения, найдите координаты точек пересечения окружности х2 + у2 = 17 и прямой 5х – 3у = 17.
4. Решите систему уравнений:
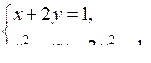
5. Изобразите на координатной плоскости множество решений системы неравенств:
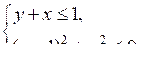
РЕШЕНИЕ ВАРИАНТОВ КОНТРОЛЬНОЙ РАБОТЫ
В а р и а н т 1
1.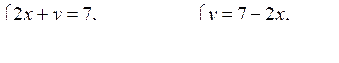
х2 – 7 + 2х = 1;
х2 + 2х – 8 = 0;
х1 = –4 у1 = 7 – 2 · (–4) = 15;
х2 = 2 у2 = 7 – 2 · 2 = 3.
О т в е т: (–4; 15), (2; 3).
2. Пусть х м – одна сторона, а у м – другая сторона прямоугольника. Так как периметр прямоугольника равен 28 м, то получим уравнение:
2(х + у) = 28.
Площадь прямоугольника равна 40 м2, поэтому ху = 40.
Составим и решим систему уравнений:
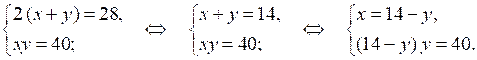
14у – у2 = 40;
у2 – 14у + 40 = 0;
у1 = 4 х1 = 14 – 4 = 10;
у2 = 10 х2 = 14 – 10 = 4.
О т в е т: 4 м и 10 м.
3. Согласно условию составим и решим систему уравнений:

х2 + х – 2 = 0;
х1 = 1 у1 = 1 + 4 = 5;
х
2 = –2 у2 = (–2)2 + 4 = 8.
О т в е т: (1; 5), (–2; 8).
4.
4у2 – 28у + 49 – 2у2 + 7у – у2 = 29;
у2 – 21у + 20 = 0;
у1 = 1 х1 = 2 · 1 – 7 = –5;
у2 = 20 х2 = 2 · 20 – 7 = 33.
О т в е т: (–5; 1), (33; 20).
5.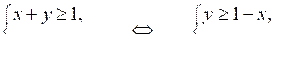
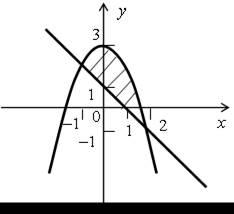
В а р и а н т 2
1.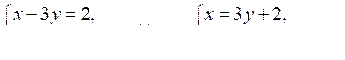
3у2 + 2у + у = 6;
3у2 + 3у – 6 = 0;
у2 + у – 2 = 0;
у1 = 1 х 1 = 3 · 1 + 2 = 5;
у2 = –2 х 2 = 3 · (–2) + 2 = –4.
О т в е т: (5; 1), (–4; –2).
2. Пусть х см – одна сторона, а у см – другая сторона прямоугольника. Так как одна из сторон прямоугольника на 2 см больше другой, то имеем уравнение х = у + 2. Так как площадь прямоугольника равна 120 см2, то имеем уравнение ху = 120.
Составим и решим систему уравнений:

у2 + 2у – 120 = 0;
у1 = 10 х1 = 10 + 2 = 12;
у2 = –12 х2 = –12 + 2 = –10 – не удовлетворяет условию задачи.
О т в е т: 10 см и 12 см.
3. Согласно условию составим и решим систему уравнений:
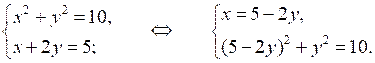
25 – 20у + 4у2 + у 2 = 10;
5у2 – 20у + 15 = 0;
у2 – 4у + 3 = 0;
у1 = 1 х1 = 5 – 2 · 1 = 3;
у2 = 3 х2 = 5 – 2 · 3 = –1.
О т в е т: (3; 1), (–1; 3).
4.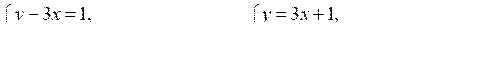
х2 – 6х2 – 2х + 9х2 + 6х + 1 = 9;
4х2 + 4х – 8 = 0;
х2 + х – 2 = 0;
х1 = 1 у1 = 3 · 1 + 1 = 4;
х2 = –2 у2 = 3 · (–2) + 1 = –5.
О т в е т: (1; 4), (–2; –5).
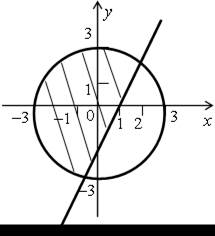
5.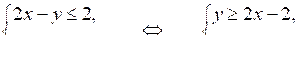
В а р и а н т 3
1.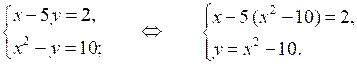
х – 5х2 + 50 = 2;
5х2 – х – 48 = 0;
D = 1 + 4 · 5 · 48 = 961;
х1 = = 3,2 у1 = 3,22 – 10 = 0,24;
х2 = = –3 у2 = 32 – 10 = –1.
О т в е т: (3,2; 0,24), (–3; –1).
2. Пусть х см – одна сторона, а у см – другая сторона прямоугольника. Согласно условию задачи составим и решим систему уравнений:
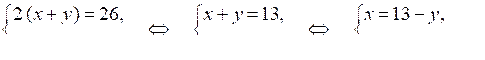
13у – у2 = 42;
у2 – 13у + 42 = 0;
у1 = 6 х1 = 13 – 6 = 7;
у2 = 7 х2 = 13 – 7 = 6.
О т в е т: 6 см и 7 см.
3.
х2 + х – 12 = 0;
х1 = 3 у1 = 32 – 8 = 1;
х2 = –4 у2 = (–4)2 – 8 = 8.
О т в е т: (3; 1), (–4; 8).
4.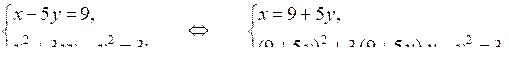
81 + 90у + 25у2 + 27у + 15у2 – у2 = 3;
39у2 + 117у + 78 = 0;
у2 + 3у + 2 = 0;
у1 = –1 х1 = 9 + 5 · (–1) = 4;
у2 = –2 х2 = 9 + 5 · (–2) = –1.
О т в е т: (4; –1), (–1; 2).
5.
В а р и а н т 4
1.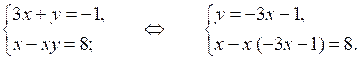
х + 3х2 + х = 8;
3х2 + 2х – 8 = 0;
D1 = 1 + 2 4 = 25;
х1 = у1 = –3 ∙ – 1 = –5;
х2 = = –2 у2 = –3 ∙ (–2) – 1 = 5.
О т в е т: , (–2; 5).
2. Пусть х м – одна сторона, а у м – другая сторона прямоугольника. Согласно условию задачи составим и решим систему уравнений:

у2 + 4у – 45 = 0;
у1 = –9 х1 = 4 – 9 = –5 – не удовлетворяет условию задачи;
у2 = 5 х2 = 4 + 5 = 9.
О т в е т: 5 м и 9 м.
3.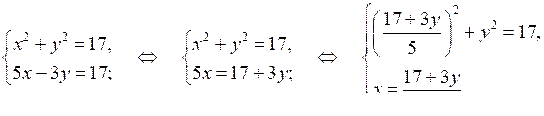
289 + 102у + 9у2 + 25у2 = 17 · 25;
34у2 + 102у – 136 = 0;
у2 + 3у – 4 = 0;
у1 = 1 х1 = = 4;
у2 = –4 х2 = = 1.
О т в е т: (4; 1), (1; –4).
4.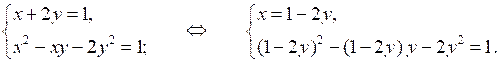
1 – 4у + 4у2 – у + 2у2 – 2у2 = 1;
4у2 – 5у = 0;
у1 = 0 х1 = 1;
у2 = х2 = 1 – 2 ∙ = –1,5.
О т в е т: (1; 0) (–1,5; 1,25).
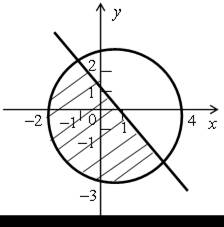
5.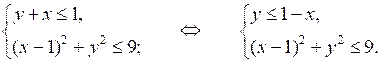
У р о к 57 Дата:
ПОНЯТИЕ ПОСЛЕДОВАТЕЛЬНОСТИ, СЛОВЕСНЫЙ
И АНАЛИТИЧЕСКИЙ СПОСОБЫ ЕЕ ЗАДАНИЯ
Цели: ввести понятие последовательности, конечной и бесконечной; рассмотреть последовательности, заданные словесно и с помощью формулы п-го члена; формировать умение находить п-й член последовательности по заданной формуле.
Ход урока
I. Организационный момент.
II. Объяснение нового материала.
Учение о последовательностях и их частном случае – прогрессиях – является существенной, хотя и несколько изолированной, частью курса алгебры. Для создания представления о последовательностях следует начать с рассмотрения конкретных примеров:
П р и м е р 1.
2; 4; 6; 8; …
Сразу обращаем внимание учащихся, что числа записаны в определенном порядке. Словесно эту последовательность можно описать (задать) так: «последовательность четных положительных чисел». Просим назвать число, которое будет стоять в этой последовательности на пятом месте, на восьмом, на сотом. Замечаем, что если «место» числа в последовательности обозначить натуральным числом п, то вычислить это число можно, оно равно 2п.
П р и м е р 2.
Последовательность правильных дробей с числителем равным 1. Для любого натурального числа п можно указать соответствующую дробь, стоящую в этой последовательности на п-ом месте – она равна . Теперь легко вычислить, что на седьмом месте должна стоять дробь , на тридцатом – дробь , на тысячном – дробь .
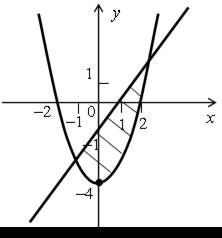
3. Не выполняя построения, найдите координаты точек пересечения параболы у = х2 – 8 и прямой х + у = 4.
4. Решите систему уравнений:
5. Изобразите на координатной плоскости множество решений системы неравенств:
В а р и а н т 4
1. Решите систему уравнений:
2. Одна из сторон прямоугольника на 4 м больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 45 м2.
3. Не выполняя построения, найдите координаты точек пересечения окружности х2 + у2 = 17 и прямой 5х – 3у = 17.
4. Решите систему уравнений:
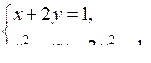
5. Изобразите на координатной плоскости множество решений системы неравенств:
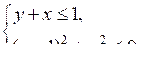
РЕШЕНИЕ ВАРИАНТОВ КОНТРОЛЬНОЙ РАБОТЫ
В а р и а н т 1
1.
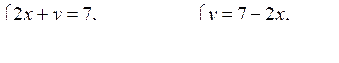
х2 – 7 + 2х = 1;
х2 + 2х – 8 = 0;
х1 = –4 у1 = 7 – 2 · (–4) = 15;
х2 = 2 у2 = 7 – 2 · 2 = 3.
О т в е т: (–4; 15), (2; 3).
2. Пусть х м – одна сторона, а у м – другая сторона прямоугольника. Так как периметр прямоугольника равен 28 м, то получим уравнение:
2(х + у) = 28.
Площадь прямоугольника равна 40 м2, поэтому ху = 40.
Составим и решим систему уравнений:
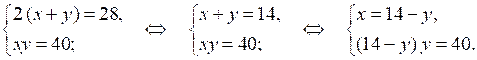
14у – у2 = 40;
у2 – 14у + 40 = 0;
у1 = 4 х1 = 14 – 4 = 10;
у2 = 10 х2 = 14 – 10 = 4.
О т в е т: 4 м и 10 м.
3. Согласно условию составим и решим систему уравнений:

х2 + х – 2 = 0;
х1 = 1 у1 = 1 + 4 = 5;
х
2 = –2 у2 = (–2)2 + 4 = 8.
О т в е т: (1; 5), (–2; 8).
4.
4у2 – 28у + 49 – 2у2 + 7у – у2 = 29;
у2 – 21у + 20 = 0;
у1 = 1 х1 = 2 · 1 – 7 = –5;
у2 = 20 х2 = 2 · 20 – 7 = 33.
О т в е т: (–5; 1), (33; 20).
5.
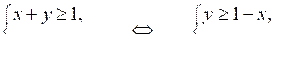

В а р и а н т 2
1.
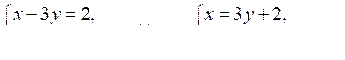
3у2 + 2у + у = 6;
3у2 + 3у – 6 = 0;
у2 + у – 2 = 0;
у1 = 1 х 1 = 3 · 1 + 2 = 5;
у2 = –2 х 2 = 3 · (–2) + 2 = –4.
О т в е т: (5; 1), (–4; –2).
2. Пусть х см – одна сторона, а у см – другая сторона прямоугольника. Так как одна из сторон прямоугольника на 2 см больше другой, то имеем уравнение х = у + 2. Так как площадь прямоугольника равна 120 см2, то имеем уравнение ху = 120.
Составим и решим систему уравнений:

у2 + 2у – 120 = 0;
у1 = 10 х1 = 10 + 2 = 12;
у2 = –12 х2 = –12 + 2 = –10 – не удовлетворяет условию задачи.
О т в е т: 10 см и 12 см.
3. Согласно условию составим и решим систему уравнений:
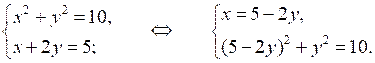
25 – 20у + 4у2 + у 2 = 10;
5у2 – 20у + 15 = 0;
у2 – 4у + 3 = 0;
у1 = 1 х1 = 5 – 2 · 1 = 3;
у2 = 3 х2 = 5 – 2 · 3 = –1.
О т в е т: (3; 1), (–1; 3).
4.
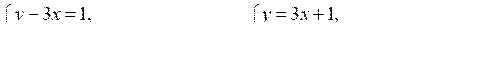
х2 – 6х2 – 2х + 9х2 + 6х + 1 = 9;
4х2 + 4х – 8 = 0;
х2 + х – 2 = 0;
х1 = 1 у1 = 3 · 1 + 1 = 4;
х2 = –2 у2 = 3 · (–2) + 1 = –5.
О т в е т: (1; 4), (–2; –5).
5.
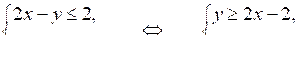

В а р и а н т 3
1.
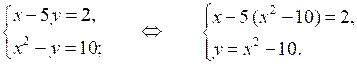
х – 5х2 + 50 = 2;
5х2 – х – 48 = 0;
D = 1 + 4 · 5 · 48 = 961;
х1 = = 3,2 у1 = 3,22 – 10 = 0,24;
х2 = = –3 у2 = 32 – 10 = –1.
О т в е т: (3,2; 0,24), (–3; –1).
2. Пусть х см – одна сторона, а у см – другая сторона прямоугольника. Согласно условию задачи составим и решим систему уравнений:
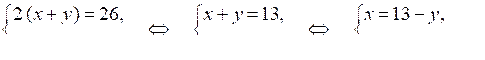
13у – у2 = 42;
у2 – 13у + 42 = 0;
у1 = 6 х1 = 13 – 6 = 7;
у2 = 7 х2 = 13 – 7 = 6.
О т в е т: 6 см и 7 см.
3.

х2 + х – 12 = 0;
х1 = 3 у1 = 32 – 8 = 1;
х2 = –4 у2 = (–4)2 – 8 = 8.
О т в е т: (3; 1), (–4; 8).
4.
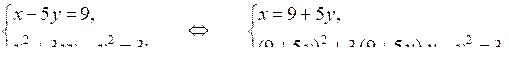
81 + 90у + 25у2 + 27у + 15у2 – у2 = 3;
39у2 + 117у + 78 = 0;
у2 + 3у + 2 = 0;
у1 = –1 х1 = 9 + 5 · (–1) = 4;
у2 = –2 х2 = 9 + 5 · (–2) = –1.
О т в е т: (4; –1), (–1; 2).
5.


В а р и а н т 4
1.
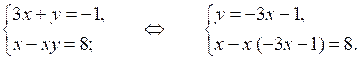
х + 3х2 + х = 8;
3х2 + 2х – 8 = 0;
D1 = 1 + 2 4 = 25;
х1 = у1 = –3 ∙ – 1 = –5;
х2 = = –2 у2 = –3 ∙ (–2) – 1 = 5.
О т в е т: , (–2; 5).
2. Пусть х м – одна сторона, а у м – другая сторона прямоугольника. Согласно условию задачи составим и решим систему уравнений:

у2 + 4у – 45 = 0;
у1 = –9 х1 = 4 – 9 = –5 – не удовлетворяет условию задачи;
у2 = 5 х2 = 4 + 5 = 9.
О т в е т: 5 м и 9 м.
3.
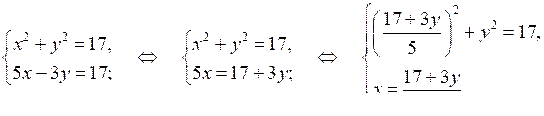
289 + 102у + 9у2 + 25у2 = 17 · 25;
34у2 + 102у – 136 = 0;
у2 + 3у – 4 = 0;
у1 = 1 х1 = = 4;
у2 = –4 х2 = = 1.
О т в е т: (4; 1), (1; –4).
4.
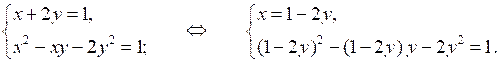
1 – 4у + 4у2 – у + 2у2 – 2у2 = 1;
4у2 – 5у = 0;
у1 = 0 х1 = 1;
у2 = х2 = 1 – 2 ∙ = –1,5.
О т в е т: (1; 0) (–1,5; 1,25).
5.
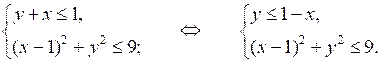

У р о к 57 Дата:
ПОНЯТИЕ ПОСЛЕДОВАТЕЛЬНОСТИ, СЛОВЕСНЫЙ
И АНАЛИТИЧЕСКИЙ СПОСОБЫ ЕЕ ЗАДАНИЯ
Цели: ввести понятие последовательности, конечной и бесконечной; рассмотреть последовательности, заданные словесно и с помощью формулы п-го члена; формировать умение находить п-й член последовательности по заданной формуле.
Ход урока
I. Организационный момент.
II. Объяснение нового материала.
Учение о последовательностях и их частном случае – прогрессиях – является существенной, хотя и несколько изолированной, частью курса алгебры. Для создания представления о последовательностях следует начать с рассмотрения конкретных примеров:
П р и м е р 1.
2; 4; 6; 8; …
Сразу обращаем внимание учащихся, что числа записаны в определенном порядке. Словесно эту последовательность можно описать (задать) так: «последовательность четных положительных чисел». Просим назвать число, которое будет стоять в этой последовательности на пятом месте, на восьмом, на сотом. Замечаем, что если «место» числа в последовательности обозначить натуральным числом п, то вычислить это число можно, оно равно 2п.
П р и м е р 2.
Последовательность правильных дробей с числителем равным 1. Для любого натурального числа п можно указать соответствующую дробь, стоящую в этой последовательности на п-ом месте – она равна . Теперь легко вычислить, что на седьмом месте должна стоять дробь , на тридцатом – дробь , на тысячном – дробь .